4. Нестационарные временные ряды. Два вида нестационарности. Проблема единичного корня. Тесты Дики-Фуллера. Нестационарные временные ряды

Многие временные ряды нестационарны. Большинство экономических данных имеют меняющиеся во времени уровни и/или дисперсии.

Многие исследователи полагают, что однородные нестационарные ряды можно преобразовать в стационарные ряды, рассматривая ряды из первых, вторых и т.д. разностей значений временного ряда.

Проблемы, связанные с нестационарностью:

1. Возникновение ложной регрессии (если два независимых временных ряда имеют похожий тренд, то статистические оценки их регрессии будут довольно высокими, хотя регрессия и лишена смысла).

2. Невозможность использования стандартных распределений t-стастистики и F-статистики, как следствие, невозможно проводить проверку гипотез о значимости коэффициентов регрессии.

3. Влияние внешних шоков не угасает со временем, а наоборот, может усиливаться.

Два вида нестационарности

Случайное блуждание с дрейфом: y_t =  + y_t–1 + u_t

Модель с линейным трендом: y_t =  +  t + u_t

Здесь в обоих случаях u_t – случайное возмущение с нулевым математическим ожиданием и конечной дисперсией, то есть белый шум.

Проблема единичного корня

Среди корней характеристического уравнения нестационарного процесса есть корень, равный единице. Для анализа временного ряда на наличие единичного корня невозможно использовать АКФ или ЧАКФ.

Тесты Дики-Фуллера

Тест Дики-Фуллера проверяет стационарность временного ряда.

Существует три вида теста Дики-Фуллера.

Временной ряд без константы и без тренда

Дано уравнение временного ряда y_t =  y_t–1 + u_t.

Нулевая гипотеза Н₀: y_t = y_t–1 + u_t , т.е.  = 1 (временной ряд содержит единичный корень)

Альтернативная гипотеза Н₁: y_t =  y_t–1 + u_t,  < 1 (временной ряд стационарен)

Временной ряд с константой

Н₀: y_t = y_t–1 + u_t

Н₁: y_t = f y_t–1 + m + u_t, f < 1

Временной ряд с константой и трендом

Н₀: y_t = y_t–1 + u_t

Н₁: y_t = f y_t–1 + m + t + u_t, f < 1

Во всех трех случаях для проверки гипотезы используется статистика Дики-Фуллера. Для нахождения ее распределения используются специальные таблицы, в которых приводится два критических значения (верхнее и нижнее).

Если расчетное значение t-статистики меньше, чем 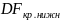, Н₀ отвергается и делается вывод о стационарности временного ряда.

Если же расчетное значение t-статистики больше, чем 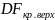, Н₀ принимается (ряд нестационарен).

Между верхним и нижним пределами — зона неопределенности. Если значение t-статистики попадает в этот промежуток, то тест Дики-Фуллера не позволяет определить, стационарен ли ряд.

5. Информационные критерии Акаике и Шварца в применении к выбору параметров модели arima.

Информационные критерии применяются для анализа верности спецификации модели. На объясняющих свойствах модели отрицательно сказывается как невключение значимой переменной, так и включение незначимой. Критерий R² в данном случае неприменим, так как для модели, в которую включено больше регрессоров, он всегда будет не меньше, чем у модели с меньшим числов регрессоров.

Наиболее распространенными информационными критериями является критерий Шварца и критерий Акаике. Оба критерия позволяют выбирать наилучшую модель из множества различных спецификаций.

Критерий Акаике:

Критерий Шварца:

В обеих формулах n – это объем выборки, m – число коэффициентов в модели регрессии (с учетом константы), 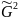- оценка максимального правдоподобия дисперсии остатков регрессионной модели.

Предпочтение отдается той модели, у которой значение информационного критерия минимально.

Нечто подобное нужно было выполнить в домашнем задании, но там была модель ARMA. Суть, однако, та же.