Лекция № 6. Численное дифференцирование.
1. Вычисление производной по её определению.
Пусть функция
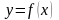определена в некоторой окрестности
точки
и имеет производную в этой точке, то
есть существует предел отношения функции
к приращению аргумента при стремлении
последнего к нулю.
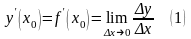
Значение
производной в точке
можно
получить, переходя к пределу в (1) по
последовательности целых чисел п и
полагая, например,
.
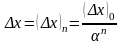Здесь
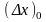- некоторое начальное приращение
аргумента,
- некоторое число, большее единицы,
.
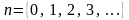Тогда значение производной функции
в точке
запишется так:
.
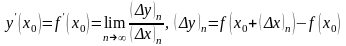Отсюда получаем приближённое равенство
.
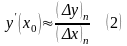Для функции , имеющей непрерывную производную до второго порядка включительно в окрестности точки , точность приближения можно установить, воспользовавшись формулой Тейлора:
.
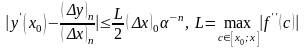Для достижения заданной точности приближения производной можно при определённом (конечном) числе вычислений использовать неравенство:
.
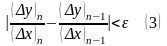Пример 1. Вычислить
производную функции
в точке
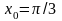с точностью
.
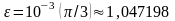Решение. Положим
,
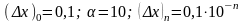откуда:
.
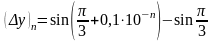Определим приближённое значение производной:
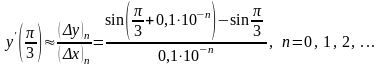
Найдём отношения, аппроксимирующие производную:
.
Заметим, что
.
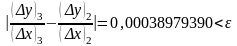Таким образом, начиная с третьего
приближения, в соответствии с оценкой
(3), получаем искомое приближение
производной данной функции с точностью
не меньшей заданной. Точное значение
.
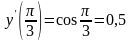2. Конечно-разностные аппроксимации.
Пусть отрезок
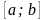разбит на п равных частей точками
.
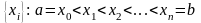Разность расстояний между
соседними значениями аргумента постоянна,
то есть шаг
.
Далее, пусть на отрезке
определена функция
,
значения которой в точках
равны
.
Запишем выражения для первой производной данной функции в точке с помощью отношения конечных разностей следующих типов:
а) аппроксимация с помощью разностей вперёд (правых разностей)
;
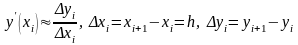
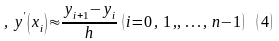б) аппроксимация с помощью разностей назад (левых разностей)
;
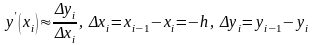
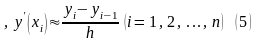в)
аппроксимация с помощью центральных
разностей (точка
является центром системы точек
):
.
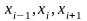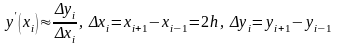
Очевидно, что аппроксимация
производной с помощью центральных
разностей представляет собой среднее
арифметическое отношений (4) и (5) в точках
.
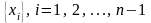Отметим, что соотношения (4) и (6) не
позволяют вычислить значение производной
в правом конце отрезка а, а соотношения
(5) и (6) – в левом конце отрезка
.
Можно показать, что для
функции
,
имеющей непрерывную производную до
второго порядка включительно, погрешность
аппроксимации производных разностями
вперёд и назад имеет один и тот же порядок
,
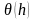а погрешность аппроксимации центральными
разностями для функции, имеющей
непрерывную производную до третьего
порядка включительно, имеет порядок
.
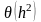Приближённое значение
производной второго порядка в точке
выразим через значения функции
.
Для этого представим вторую производную
с помощью правой разности:
,
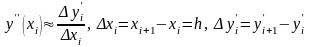а производные первого порядка
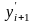и
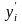- с помощью левых разностей:
и окончательно получим:
.
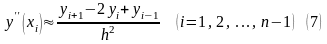Погрешность последней аппроксимации имеет порядок для функции , имеющей непрерывную производную до четвёртого порядка включительно на отрезке . Естественно, представление (7) позволяет вычислять значения производной с помощью конечных разностей только во внутренних точках отрезка.