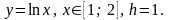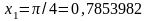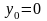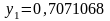- •Содержание комплекса.
- •Примерный тематический план дисциплины “Численные методы”.
- •Содержание дисциплины “Численные методы”.
- •Тема 1. Численные методы решения нелинейных уравнений.
- •Тема 2. Аппроксимация функций. Интерполяция функций.
- •Тема 3. Численное дифференцирование. Численное интегрирование. Численные методы решения дифференциальных уравнений.
- •Справочная литература.
- •Часть вторая. Конспект лекций по дисциплине “Численные методы”.
- •Лекция №1. Решение нелинейных уравнений. Метод половинного деления.
- •Лекция № 2. Метод итераций для одного уравнения с одним неизвестным.
- •Лекция № 3. Аппроксимация функций. Метод наименьших квадратов.
- •Лекция № 4. Интерполирование функций. Формула Лагранжа.
- •Лекция № 5. Интерполирование функций кубическими сплинами.
- •Лекция № 6. Численное дифференцирование.
- •Лекция № 7. Численное интегрирование.
- •Лекция № 8. Численные методы безусловной оптимизации.
- •Понятие о численном решении задачи Коши.
- •Часть третья. Вопросы к зачёту по дисциплине “Численные методы”.
- •Часть четвёртая. Примеры практических заданий к зачёту по дисциплине “Численные методы”.
- •Часть пятая. Варианты практических заданий зачёту по численным методам.
- •Варианты заданий для практической работы.
- •Задача № 2.
- •Задача № 3.
- •Задача № 4.
- •Задача № 5.
- •Задача № 6.
- •Задача № 7.
- •Задача № 8.
- •Задача № 9.
- •Задача № 10
- •Список используемой литературы:
Лекция № 5. Интерполирование функций кубическими сплинами.
Пусть отрезок
разбит на
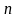 частей точками
частей точками
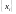 :
:
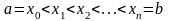
Сплином (иначе – сплайном)
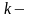 й
степени называется функция, представляющая
собой многочлен степени не выше
на каждом из последовательно примыкающих
друг к другу интервалов
й
степени называется функция, представляющая
собой многочлен степени не выше
на каждом из последовательно примыкающих
друг к другу интервалов
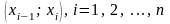 ,
причём во всех точках стыка двух
интервалов
,
причём во всех точках стыка двух
интервалов
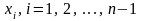 функция
непрерывна вместе со своими производными
до порядка не выше
.
функция
непрерывна вместе со своими производными
до порядка не выше
.
Например, непрерывная кусочно-линейная функция (графиком которой является ломаная) является сплином первой степени с производной, терпящей разрыв в точках излома.
Пусть на отрезке
определена функция
,
значения которой в точках
равны
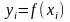 .
.
Задача интерполяции функции
на отрезке
кубическим сплином (сплайном третьей
степени) состоит в нахождении функции
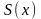 ,
равной многочлену третьей степени
,
равной многочлену третьей степени
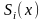 на каждом отрезке
на каждом отрезке
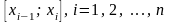 ,
то есть
,
то есть
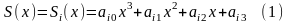 ,
,
причём значения сплина в узлах интерполяции равны соответствующим значениям заданной функции и сплин-функция непрерывна в узлах интерполяции вместе со своими производными первого и второго порядков:
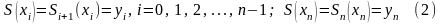 ;
;
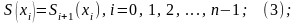
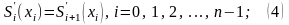 ;
;
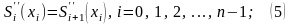 .
.
Условия (2) – (5) дают
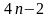 линейных алгебраических уравнений для
определения
линейных алгебраических уравнений для
определения
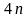 неизвестных коэффициентов
неизвестных коэффициентов
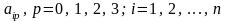 при соответствующих степенях
в многочленах
при соответствующих степенях
в многочленах
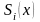 .
.
Можно показать, что интерполяционный кубический сплин для функции существует и является единственным, если вместе с уравнениями (2) – (5) удовлетворяется пара дополнительных (краевых) условий следующего типа:
I.
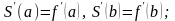
II.
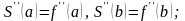
III.
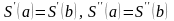 .
.
Рассмотрим случай разбиения
отрезка
на
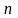 равных частей с шагом
равных частей с шагом
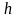 ,
для которого
,
для которого
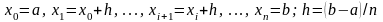 .
Разберём подробно построение
интерполяционного кубического сплина
для условия типа I.
.
Разберём подробно построение
интерполяционного кубического сплина
для условия типа I.
При построении сплина,
удовлетворяющего краевым условиям типа
I, введём величины
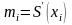 ,
называемые иногда наклонами сплайна в
узлах интерполяции.
,
называемые иногда наклонами сплайна в
узлах интерполяции.
Можно показать, что интерполяционный кубический сплин вида
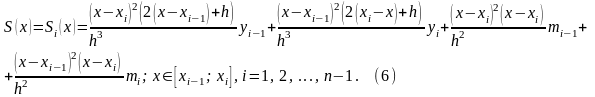
удовлетворяет условиям (2),
(3), (4) для любых
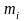 .
Из условия (5) и краевых условий I
можно определить
параметр
.
.
Из условия (5) и краевых условий I
можно определить
параметр
.
Действительно, легко проверить,
что
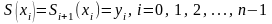 .
Кроме того, вычисления показывают, что
.
Кроме того, вычисления показывают, что
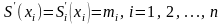 и
и
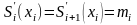 .
.
Если учесть, что
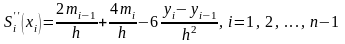 ,
,
и
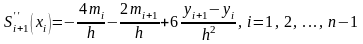 ,
,
а также краевые условия типа
I и условие (5), то получим
систему из
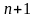 линейных уравнений относительно
неизвестных
:
линейных уравнений относительно
неизвестных
:
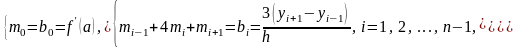
Решение этой системы позволяет найти значения неизвестных и определить интерполяционный сплин с помощью формулы (6).
Пример 1. На отрезке
построить кубический сплин, интерполирующий
функцию
с шагом
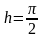 ,
удовлетворяющий на концах отрезка
краевым условиям типа I.
С помощью интерполяционной формулы
вычислить приближённое значение
,
удовлетворяющий на концах отрезка
краевым условиям типа I.
С помощью интерполяционной формулы
вычислить приближённое значение
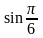 и сравнить его с точным значением.
и сравнить его с точным значением.
Решение.
Будем искать
уравнение кубической параболы
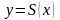 ,
удовлетворяющее следующим условиям на
концах отрезка
,
удовлетворяющее следующим условиям на
концах отрезка
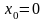 и
и
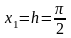 :
:
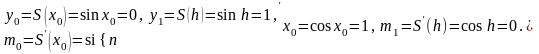
Подставив полученные значения
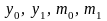 и
в формулу (6) и получим сплин вида
и
в формулу (6) и получим сплин вида
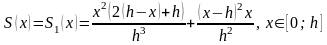 ,
,
откуда
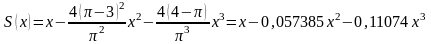 .
.
Тогда
 .
Точное значение, как известно, равно
0,5. Здесь
.
Точное значение, как известно, равно
0,5. Здесь
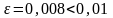 .
Как видим, в данном (достаточно простом)
примере сплин-метод обеспечивает
достаточно высокую точность приближённых
вычислений.
.
Как видим, в данном (достаточно простом)
примере сплин-метод обеспечивает
достаточно высокую точность приближённых
вычислений.
Пример 2. На отрезке
построить кубический сплин с шагом
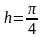 ,
интерполирующий функцию
,
если заданы значения функции в трёх
узлах интерполяции:
,
интерполирующий функцию
,
если заданы значения функции в трёх
узлах интерполяции:
|
|
|
|
|
|
|
|
С помощью интерполяционной формулы вычислить приближённое значение и сравнить с точным значением.
Решение.
Представим сплин в виде (6):

При таком представлении должны удовлетворяться уравнения системы (7):
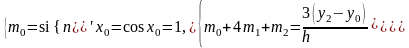 где
.
где
.
Заметим, что
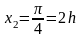 .
Тогда имеем:
.
Тогда имеем:
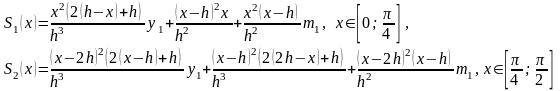 .
.
Учитывая, что
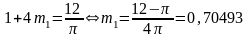 ,
получим после преобразований:
,
получим после преобразований:
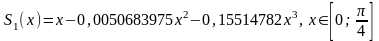 ;
;
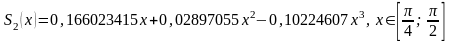 .
.
Тогда
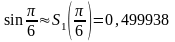 .
Здесь
.
Здесь
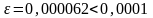 - весьма высокая точность. Из данных
примеров видно, что чем больше количество
узлов интерполяции, тем выше точность
приближённых вычислений.
- весьма высокая точность. Из данных
примеров видно, что чем больше количество
узлов интерполяции, тем выше точность
приближённых вычислений.
Задание.
Построить для указанных функций кубический сплин, интерполирующий их на данном отрезке с заданным шагом .
1)
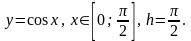 В данном задании найти приближённое
значение
В данном задании найти приближённое
значение
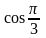 и сравнить с точным значением.
и сравнить с точным значением.
2)
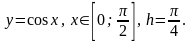
3)
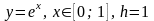 .
В данном задании найти приближённое
значение
.
В данном задании найти приближённое
значение
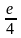 и сравнить с точным значением.
и сравнить с точным значением.
4)