Лекция № 8. Численные методы безусловной оптимизации.

1. Унимодальные функции.

Из курса математического экстремума нам известны понятия локального и глобального экстремума функции одной переменной.

Пусть дана функция , непрерывная на некотором множестве X , являющемся подмножеством множества действительных чисел R 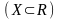. Задачей безусловной оптимизации для функции называется задача отыскания всех её локальных минимумов (максимумов) в случае, если множество X совпадает с множеством R 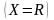. Функция называется при этом целевой функцией.

Аналогично данная задача формулируется для функции двух и более переменных, для множества .

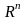Мы рассмотрим численные методы решения данной задачи для нахождения минимума функции одной переменной. Задачу отыскания локального минимума целевой функции символически записывают так: .

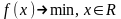Определение. Непрерывная функция называется унимодальной на отрезке , если:

1. точка локального минимума функции принадлежит отрезку ;

2. для любых двух точек отрезка 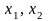взятых по одну сторону от точки минимума, точке, более близкой к точке минимума соответствует меньшее значение функции; то есть из услови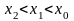й или следует условие .

Достаточное условие унимодальности функции на отрезке содержится в следующей теореме.

Теорема. Если функция дважды дифференцируема на отрезке и 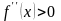в любой точке этого отрезка, то данная функция является унимодальной на отрезке .

Заметим, что условие определяет выпуклость вниз (вогнутость) функции на указанном отрезке.

Пример 1. Для функции найти:

1. промежуток Х, на котором функция является унимодальной;

2. решение задачи .

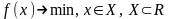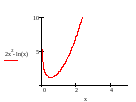
Решение.

Функция определена при 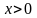; найдём её производные: 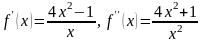. Заметим, что при 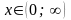. Следовательно, функция унимодальна на интервал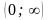е . Далее, при . Знаки производной меняются в окрестностях точки 0,5 с “- “ на “+”, поэтому, согласно достаточном условию экстремума, данная точка является точкой локального минимума.

2. Схема сужения промежутка унимодальности функции.

Пусть требуется решить задачу

(1)

Применение численных методов для отыскания точек локального минимума предполагает:

1. определение промежутков унимодальности функции, то есть нахождение отрезков, каждому из которых принадлежит одна точка локального минимума;

2. вычисление значения , принадлежащего выбранному промежутку, с заданной точностью.

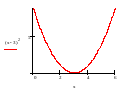
Для непрерывной функции строят её график на некотором отрезке и, если окажется, что на этом отрезке график функции имеет вид, изображённый на рисунке, то - отрезок унимодальности функции. Отрезок берётся, по возможности, малым.

При вычислении точки минимума точность достигается последовательным уменьшением отрезка , содержащего точку , до размеров, не превышающих заданную точность .

Замечание. Если функция имеет производную во всей области определения, то для отыскания её стационарных точек нужно решить уравнение 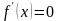. Для решения этого уравнения, как правило, необходимо использовать численные методы, описанные в лекциях 1 и 2. Однако, для решения задачи (1) проще применять прямые численные методы поиска минимума функции .

Рассмотрим один из приёмов, позволяющих сузить отрезок унимодальности функции. Пусть функция унимодальна на отрезке . Возьмём две произвольные точки и , принадлежащие этому отрезку и такие, что 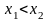. Возможны, очевидно, следующие три случая, в каждом из которых можно указать отрезок меньших размеров 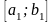, содержащий точку минимума и принадлежащий первоначальному отрезку.

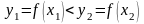1. Если , то положим 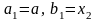и получим меньший отрезок унимодальности .

2. Если 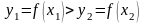, то положим .

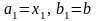3. Если , то, очевидно, .

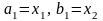Пример 2. Для функции , выбрав отрезок унимодальности 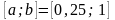и две произвольные точки 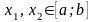, найти меньший отрезок унимодальности .

Решение.

В примере 1 было установлено, что данная функция имеет точку минимума и является унимодальной на любом отрезке, содержащем эту точку и лежащем в области её определения . Возьмём ; тогда:

.

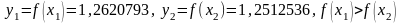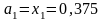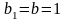Здесь естественно положить и (случай II). Получили новый, меньший отрезок унимодальности .

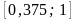Методы, с помощью которых вычисляют значения точки минимума функции одной переменной, отличаются алгоритмами выбора точек и для локализации точки с заданной точностью.

3. Метод половинного деления.

Пусть при решении задачи (1) определён отрезок , которому принадлежит точка локального минимума , и функция унимодальна на этом отрезке.

Далее для сужения отрезка унимодальности используем точки и , расположенные симметрично относительно середины данного отрезка:

.

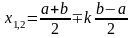Будем считать, что число k гораздо меньше единицы 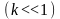. Тогда точки и принадлежат отрезку и, следуя рассмотренной в предыдущем пункте схеме, получим новый суженный отрезок и оценим его длину в каждом из трёх возможных случаев:

I. ;

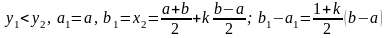II. ;

III. .

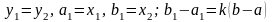Таким образом, после первого шага преобразований найден новый отрезок унимодальности , длина которого уменьшилась.

Названия метода (метод половинного деления) мотивировано тем, что если величина k очень мала, то длина отрезка унимодальности уменьшается почти вдвое (в случаях I и II).

Теперь в новом суженном промежутке выберем точк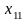и и 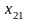, симметричные относительно его середины:

.

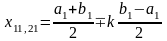Произведя вычисления, аналогичные проделанным ранее, получаем отрезок 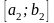, длина которого не больше, чем

,

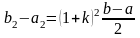и так далее.

В результате приходим к последовательности таких вложенных отрезков 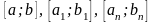, что точка локального минимума функции принадлежит каждому из них и является общим пределом последовательностей и .

Отсюда получаются приближённые равенс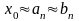тва: , оценить точность которых на п-м шаге вычислений можно с помощью неравенства:

.

Пример 3. Найти точку локального минимума функции на отрезке 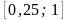методом половинного деления с точностью 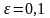. Провести вычисления, полагая и предварительно оценив минимальное число шагов, необходимое для достижения указанной точности.

Решение.

В примере 1 было установлено, что функция унимодальна на отрезке ; точка принадлежит этому отрезку. Воспользуемся неравенством (2) и определим число шагов п:

.

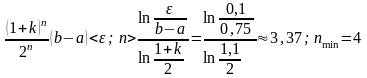Введём обозначения:

.

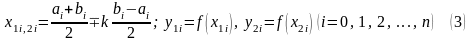Здесь 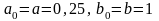, 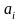и - координаты начала и конца отрезка, полученного на 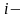м шаге вычислений, точки 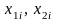принадлежат отрезку .

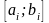Проведём последовательные вычисления.

1. Отрезок :

.

2. Отрезок :

.

3. Отрезок :

.

4. Отрезок :

.

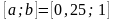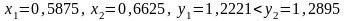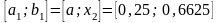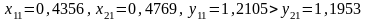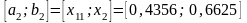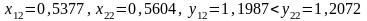5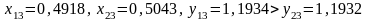. Отрезок .

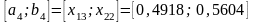Разность 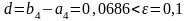. Следовательно, точкой локального минимума, найденной с заданной точностью, является .

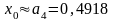Задание.

Для заданной целевой функции найти промежуток 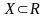, на котором она унимодальна. Найти точное решение задачи минимизации . Найти приближённое решение этой задачи с точностью методом половинного деления.

1. ;

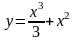2. ;

3. ;

4. .

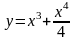Лекция № 9. Численное решение дифференциальных уравнений первого порядка.