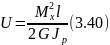- •Ведомость объема дипломной работы
- •Реферат
- •Содержание
- •1 Описание станка лазерной резки металла lasercut-4015-3 8
- •2 Постановка задачи 14
- •3 Пространственный (касой) изгиб балок, кручение стержней (брусьев) 15
- •4 Моделирование процесса работы оптической лазерной головки 32
- •5. Расчет экономической эффективности 40
- •6 Охрана труда 46
- •Введение
- •Описание станка лазерной резки металла lasercut-4015-3
- •Постановка задачи
- •Пространственный (касой) изгиб балок, кручение стержней (брусьев)
- •Моделирование процесса работы оптической лазерной головки
- •Расчет экономической эффективности
- •Износ инструмента и приспособлений целевого назначения
- •Общепроизводственные расходы
- •Общехозяйственные расходы
- •Расчет цены на обработанный лист металла
- •Результаты расчетов
- •Охрана труда
- •Заключение список используемых литературных источников
- •Приложение а
Постановка задачи
Нужно получить минимальные перемещения координатных осей лазера, когда они расположены в местах возникновения мах перемещений. Для этого:
рассчитать координатные оси первоначальной лазерной головки
изучить полученные перемещения, они не должны превышать 0.15 мм
после полученных результатов, если они превышают, модернизировать нашу конструкцию и пересчитать снова.
Модернизировать модель, да тех пор, если не будут достигнуты нужные результаты.
Пространственный (касой) изгиб балок, кручение стержней (брусьев)
Косым называют изгиб, при котором плоскость действия изгибающего момента, возникающего в сечении, не совпадает ни с одной из главных плоскостей бруса (при этом плоскость действия изгибающего момента обязательно должна проходить через центр тяжести сечения) (рис.5).
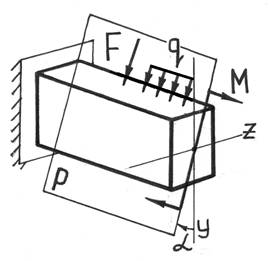
Рисунок 5 – Плоскость действия изгибающего момента
При косом изгибе изогнутая ось представляет собой плоскую кривую, и плоскость, в которой она расположена, не совпадает с плоскостью действия нагрузки. При пространственном изгибе нагрузка приложена в разных плоскостях, деформированная ось является пространственной кривой.
Определение внутренних усилий при косом изгибе
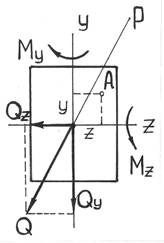
Рисунок 6 – Консольная балка
П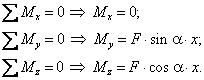 ри
косом изгибе в поперечных сечениях
бруса действуют следующие внутренние
усилия: Mz,
My
– изгибающие
моменты и Qy,
Qz
–поперечные (перерезывающие) силы. Это
легко показать, мысленно рассекая
стержень и определяя внутренние усилия
при косом изгибе консольной балки под
действием сосредоточенной силы F
на свободном конце (рис.6):
ри
косом изгибе в поперечных сечениях
бруса действуют следующие внутренние
усилия: Mz,
My
– изгибающие
моменты и Qy,
Qz
–поперечные (перерезывающие) силы. Это
легко показать, мысленно рассекая
стержень и определяя внутренние усилия
при косом изгибе консольной балки под
действием сосредоточенной силы F
на свободном конце (рис.6):
 (3.1)
(3.1)
Правило знаков для внутренних усилий: изгибающие моменты – положительны, если вызывают растяжение в положительном квадранте координатной системы zOy; поперечные силы – положительны, если под их действием отсеченный элемент поворачивается по часовой стрелке.
Таким образом, косой изгиб может быть представлен как совместное действие двух плоских изгибов в двух взаимно перпендикулярных плоскостях инерции.
Для определения полного изгибающего момента M и полной поперечной силы Q при косом изгибе достаточно определить внутренние усилия для каждого из плоских изгибов в отдельности (то есть Qy, Mz и Qz, My), а затем найти их векторную сумму

Определение напряжений при косом изгибе
Если разложить
внешние силы по главным осям инерции
Ох
и Оу,
то получим две системы сил P1x,
P2x,
…, Pnx
и P1y,
P2y,...,
Pny,
каждая из.которых вызывает прямой изгиб
с изгибающими моментами соответственно
My
и Мx
(рис.7). Применяя
принцип независимости действия сил,
нормальные напряжения
![]() (рис.8) определим как алгебраическую
сумму напряжений от Mx
и Мy:
(рис.8) определим как алгебраическую
сумму напряжений от Mx
и Мy:

Чтобы не связывать себя формальными правилами знаков, слагаемые будем определять по модулю, а знаки ставить по смыслу.
Таким образом, расчет на косой изгиб с применением принципа независимости действия сил сводится к расчету на два прямых изгиба с последующим алгебраическим суммированием напряжений.
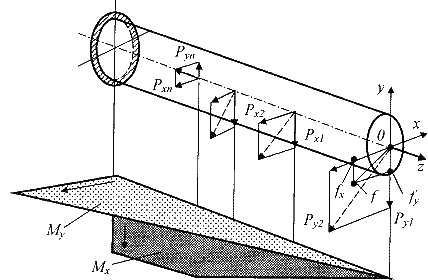 Рисунок
7 - Расчетная
модель косого изгиба бруса
Рисунок
7 - Расчетная
модель косого изгиба бруса
 Рисунок
8 - Связь
нормального напряжения с внутренними
изгибающими моментами
Рисунок
8 - Связь
нормального напряжения с внутренними
изгибающими моментами
В случае поперечных
сечений, имеющих две оси симметрии и
выступающие угловые точки (рис.9) с
равными по модулю и максимальными
одноименными координатами
![]() и
и
![]() напряжения в этих точках будут равны
напряжения в этих точках будут равны

Слагаемые в этом выражении рекомендуется определять по модулю, а знаки ставить по смыслу. Например, на рис.10 верхний ряд знаков «+» и «—» соответствует напряжениям от Мx, а нижний ряд — от My, и напряжения в этих точках будут равны:
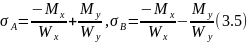
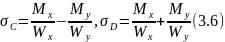
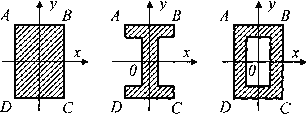
Рисунок 9 - Симметричные варианты сечений
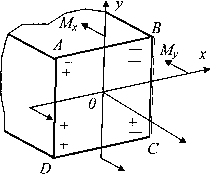 Рисунок
10 - Расстановка
знаков от действия моментов
Рисунок
10 - Расстановка
знаков от действия моментов
Условие прочности для балок из пластичного материала с указанным типом сечений запишется в виде
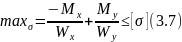
Касательные напряжения от поперечных сил, если нельзя воспользоваться формулой Журавского, допустимо не учитывать.
При проведении расчетов на прочность условие прочности составляется для опасной точки поперечного сечения, т.е. для точки, в которой нормальные напряжения достигают максимальных значений. Самой нагруженной точкой в сечении произвольной формы является точка, наиболее удаленная от нейтральной линии, разделяющей растянутую и сжатую зоны сечения.
В связи с этим, большое значение приобретают вопросы, связанные с определением положения нейтральной линии.
Положив
![]() ,
получим уравнение нейтральной линии.
,
получим уравнение нейтральной линии.
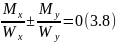
Так как напряжения в точках поперечного сечения будут пропорциональными расстояниям от нейтральной линии, то max будут возникать в наиболее удаленных от нее точках.
Силовая плоскость
– это плоскость действия результирующего
момента Мрез
(рис.11),
![]() - угол наклона силовой плоскости к
вертикали.
- угол наклона силовой плоскости к
вертикали.
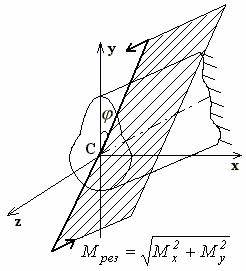
Рисунок 11 - Силовая плоскость
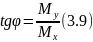
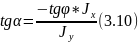
Свойства нейтральной линии
1. Если
![]() ,
то
,
то
![]() ,
то есть силовая плоскость и нейтральная
линия не являются перпендикулярными.
,
то есть силовая плоскость и нейтральная
линия не являются перпендикулярными.
2. Если
![]() ,
то из (3.10) следует, что
,
то из (3.10) следует, что
![]() ,
то есть нейтральная линия и силовая
плоскость перпендикулярны. В этом случае
стержень испытывает плоский изгиб
(примерами таких стержней являются
стержни с сечением – круг, кольцо,
квадрат).
,
то есть нейтральная линия и силовая
плоскость перпендикулярны. В этом случае
стержень испытывает плоский изгиб
(примерами таких стержней являются
стержни с сечением – круг, кольцо,
квадрат).
3. Знак «минус» в формуле (3.10) указывает, что силовая плоскость и нейтральная линия при косом изгибе проходят через противоположные квадранты.
Для определения
опасных точек сечения следует построить
касательные к контуру сечения, параллельные
нейтральной линии. Точки касания и будут
являться опасными (точки
![]() и
и
![]() на рис.12).
на рис.12).
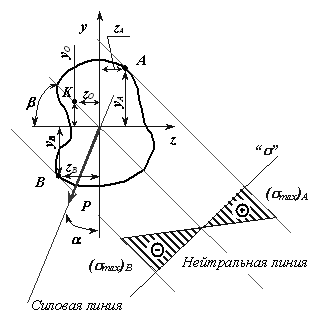
Рисунок 12 - Положение нейтральной линии при косом изгибе
Для некоторых сечений (прямоугольник, двутавр, швеллер и т.п.) наиболее напряженные точки расположены в углах этих сечений, т.е. их можно найти без определения положения нейтральной линии (рис.13).
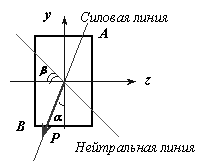
Рисунок 13 - Положение нейтральной линии и опасных точек сечения при косом изгибе для прямоугольника
Условия прочности составляют в зависимости от свойств того материала, из которого изготовлен элемент конструкции (брус).
Для хрупкого материала используют два условия прочности - для опасной точки, где имеет место растяжение (для нашего случая т. на рис.12), и для точки, где имеет место сжатие (т. )
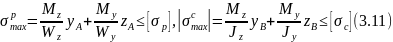
Необходимость использования двух условий прочности для хрупкого материала объясняется разными механическими свойствами материала при растяжении и сжатии. Хрупкий материал плохо сопротивляется растяжению и хорошо - сжатию.
Для пластичного материала, который одинаково сопротивляется и растяжению и сжатию, используют одно условие прочности для точки поперечного сечения, где имеют место максимальные по абсолютной величине нормальные напряжения
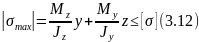
где
![]() и
и
![]() - координаты данной точки.
- координаты данной точки.
При расчетах на прочность касательными напряжениями от поперечных сил пренебрегают, т.к. их влияние незначительно.
Определение перемещений при косом изгибе
Перемещения при
косом изгибе определяют по принципу
независимости действия сил, т.е.
рассчитывают прогибы
![]() и
и
![]() в направлении главных осей, а величину
полного прогиба в любом сечении балки
получают геометрическим суммированием:
в направлении главных осей, а величину
полного прогиба в любом сечении балки
получают геометрическим суммированием:
![]() .
.
Например, для балки, изображенной на рис.14, прогиб конца консоли определится следующим образом:
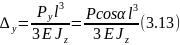
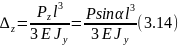
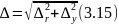
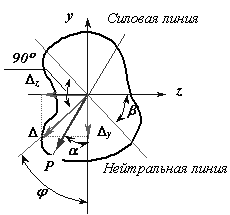
Рисунок 14 - Перемещение при косом изгибе
Направление полного
перемещения (![]() )
определится величиной отношения
)
определится величиной отношения
![]() (рис.14)
(рис.14)
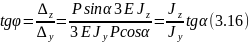
Направление полного прогиба при косом изгибе перпендикулярно нейтральной линии и не совпадает с направлением внешней силы (рис.14).
При косом изгибе (впрочем, как и при остальных видах нагружения) имеем три задачи расчета на прочность:
1) проверка прочности;
2) подбор сечения [определить Wz (размеры сечения), при заданном отношении Wz/Wy];
3) проверка по несущей способности (определить M).
Порядок проверки прочности балки, работающей в условиях косого или пространственного изгиба, тот же, что и для балки, работающей при плоском поперечном изгибе. Для этого необходимо:
- построить эпюры внутренних усилий (изгибающих моментов). Для построения эпюр внутренних усилий раскладываем нагрузки на вертикальную и горизонтальную составляющие. Вертикальная составляющая вызывает изгиб относительно горизонтальной оси , горизонтальная – относительно оси ;
- выбрать опасные сечения – это сечения, где имеет место наиболее неблагоприятное сочетание изгибающих моментов;
- в опасных сечениях найти опасные точки – точки с максимальными нормальными напряжениями;
- записать условие прочности в этих точках. Из условия прочности либо подобрать размеры поперечного сечения, либо найти допускаемую нагрузку, либо просто сделать вывод о возможности безопасной эксплуатации конструкции.
Кручение
Кручением называется вид нагружения, при котором к брусу прикладываются внешние скручивающие моменты, а в поперечных сечениях возникает единственный внутренний силовой фактор - крутящий момент Mк (рис.15).
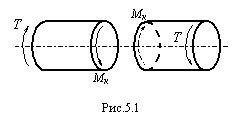
Рисунок 15 – Приложение к брусу внешних скручивающих моментов
Брусья, передающие крутящий момент называются валами. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п. В большинстве случаев бывают заданы мощность, передаваемая валом, и числом оборотов, а величины скручивающих моментов определяются исходя из этих данных.
Пусть вал вращается
с постоянной скоростью n об/мин. и передает
мощность N Нм/с. Угловая скорость вращения
вала равна
![]() (рад/сек), а передаваемая мощность
(рад/сек), а передаваемая мощность
![]() .
Скручивающий момент равен
.
Скручивающий момент равен
![]() .
.
Построение эпюр крутящих моментов
Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.
Крутящий момент Мк в сечении вала числено равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения, при этом могут рассматриваться как левая, так и правая отсеченные части вала.
Рассмотрим вал, нагруженный скручивающими моментами Т1=10кН×м, Т2=25 кН×м, Т3=35 кН×м (рис.16). Воспользуемся методом сечений. Рассечем участки вала (рис.16). Границами участков являются точки приложения скручивающих моментов. Отбросим правую отсеченную часть. Заменим ее крутящим моментом Мк.
Из уравнения равновесия отсеченной части найдем величину крутящего момента Мк, возникающего в сечении
I участок
участок
![]()
![]() ,
,
Mк1 = 0 .
II
участок
![]()
![]() ,
,
Mк2 = T1 = 10 кНм.
III
участок
![]()
![]() Mк3
= T1
+T2
= 35 кНм.
Mк3
= T1
+T2
= 35 кНм.
Для наглядного представления о величине крутящих моментов и характере их распределения по длине вала построим эпюры этих моментов. Построение эпюр крутящих моментов аналогично построению эпюр продольных сил при осевом растяжении-сжатии (рис.17).
Заметим, что в местах приложения внешних моментов ординаты эпюры скачкообразно изменяются на величину приложенного внешнего момента.
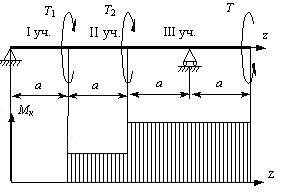
Рисунок 17 – Построение эпюр крутящих моментов
Напряжения в поперечном сечении
Опыты показывают, что если на поверхности бруса круглого сечения нанести прямоугольную сетку, а на торцевой поверхности нанести радиальные линии (рис.18), то после деформации кручение окажется что:
· все образующие поворачиваются на один и тот же угол g, а прямоугольники, нанесенные на поверхности, превращаются в параллелограммы;
· торцевые сечения остаются круглыми, плоскими, расстояния между ними не меняются;
· каждое сечение поворачивается относительно другого на некоторый угол j, называемый углом закручивания;
· радиальные линии на торцевой поверхности остаются прямыми.
На основании этих наблюдений можно заключить, что может быть принята гипотеза Бернулли (гипотеза плоских сечений), а в вале возникают условия чистого сдвига, в поперечных сечениях действуют только касательные напряжения, нормальные напряжения равны нулю.
Рассмотрим поперечное сечение вала, расположенное на некотором расстоянии z от торцевого, где Мк= T (рис.18). На элементарной площадке dF будет действовать элементарная сила tdF, момент который относительно оси вала равен (tdF)×r. Крутящий момент Мк, в сечении равен
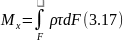
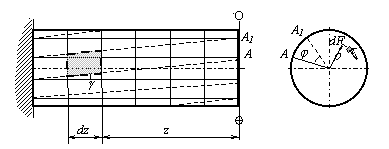
Рисунок 18 - Поперечное сечение вала
Для того чтобы проинтегрировать это выражение необходимо знать закон распределения напряжений в сечении. Выделим из вала элементарное кольцо длиной dz и толщиной dr (рис.19).
Правый торец элемента повернется относительно левого на угол dj, образующая СВ повернется на угол g и займет положение СВ1. Угол g - относительный сдвиг. Из треугольника ОВВ1 найдем:
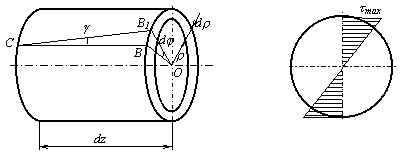
Рисунок 19 – Вал
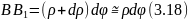
Из треугольника
СВВ1:
![]() .
Откуда, приравнивая правые части, получим
.
Откуда, приравнивая правые части, получим
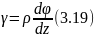
На основании закона Гука при сдвиге:
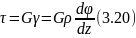
Подставим выражение (3.20) в (3.17):
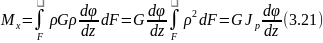
Откуда
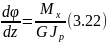
Подставим значение
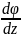 в выражение (3.20) получим:
в выражение (3.20) получим:
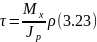
Таким образом, касательные напряжения при кручении прямо пропорциональны расстоянию от центра тяжести сечения до рассматриваемой точки и одинаковы в точках, одинаково удаленных от центра тяжести сечения (рис. 19). При r = 0 получим t = 0. Наибольшие напряжения возникают в точках контура сечения при r = R:
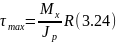
Величина отношения полярного момента инерции к радиусу вала называется моментом сопротивления сечения при кручении или полярным моментом сопротивления
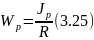
Для сплошного круглого сечения
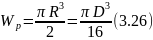
Для кольцевого сечения
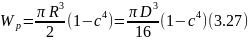
где
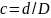 .
.
Тогда максимальные касательные напряжения равны
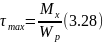
Условие прочности при кручении вала
Условие прочности при кручении с учетом принятых обозначений формулируется следующим образом: максимальные касательные напряжения, возникающие в опасном сечении вала, не должны превышать допускаемых напряжений и записывается в виде
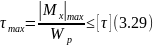
Из условия прочности можно определить диаметр вала:
- сплошного сечения
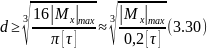
- кольцевого сечения
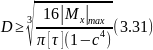
Как следует из
закона парности касательных напряжений,
одновременно с касательными напряжениями,
действующими в плоскости поперечного
сечения вала, имеют место касательные
напряжения в продольных плоскостях.
Они равны по величине парным напряжениям,
но имеют противоположный знак. Таким
образом, все элементы бруса при кручении
находятся в состоянии чистого сдвига.
Так как чистый сдвиг является частным
случаем плоского напряженного состояния,
при котором
![]() ,
,
![]() ,
,
![]() ,
то при повороте граней элемента на 450
в новых площадках обнаруживаются только
нормальные напряжения, равные по величине
t
(рис.20).
,
то при повороте граней элемента на 450
в новых площадках обнаруживаются только
нормальные напряжения, равные по величине
t
(рис.20).
Рассмотрим возможные виды разрушения валов, изготовленных из различных материалов при кручении. Валы из пластичных материалов чаще всего разрушаются по сечению, перпендикулярному к оси вала, под действием касательных напряжений, действующих в этом сечении (рис.21а). Валы из хрупких материалов, разрушаются по винтовой поверхности наклоненной к оси вала под углом 450, т.е. по направлению действия максимальных растягивающих напряжений (рис.21б). У деревянных валов первые трещины возникают по образующим цилиндра, так как древесина плохо сопротивляется действию касательных напряжений, направленных вдоль волокон (рис.21в).

Рисунок 20 – Нормальные напряжения Рисунок 21 – Растягивающие напряжения
Таким образом,
характер разрушения зависит от способности
материала вала сопротивляться воздействию
нормальных и касательных напряжений.
В соответствии с этим, допускаемые
касательные напряжения принимаются
равным![]() - для хрупких материалов и
- для хрупких материалов и
![]() - для пластичных материалов.
- для пластичных материалов.
Рациональная форма сечения вала
Анализируя эпюру касательных напряжений (рис.20) можно отметить, что наибольшие напряжения возникают на поверхности вала, в центральной части они значительно меньше и на продольной оси равны нулю. Следовательно, в сплошном валу материал, находящийся в центральной части в значительной степени недогружен, его вклад в прочность вала мал. Поэтому рациональным для валов считается кольцевое сечение.
Деформации при кручении и условие жесткости
Из выражения (3.22) следует, что
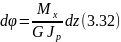
интегрируя которое по длине вала, получим:

Если крутящий момент и величина
Если Мк
= const
и
![]() =
const
по всей длине вала, то
=
const
по всей длине вала, то
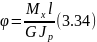
где - жесткость вала при кручении.
Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания
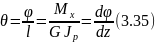
Для обеспечения требуемой жесткости вала необходимо, чтобы наибольший относительный угол закручивания не превосходил допускаемого:
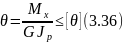
Эта формула выражает
условие жесткости вала при кручении.
Обычно принимается
![]() на 1 м длины вала.
на 1 м длины вала.
Потенциальная энергия деформации при кручении
Элементарная
работа статически приложенного внешнего
момента Т на перемещении
![]() равна:
равна:
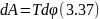
При чистом кручении
Мк
= Т и
![]() .
.
Потенциальная энергия деформации
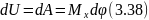
интегрируя выражение для элементарной работы по всей длине l стержня, получим
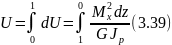
При Мк = const и = const, получим