2. 5. Принцип реактивного движения. Уравнение движения тела с переменной массой. @

Особый интерес представляет применение закона сохранения импульса к яв­лению «непрерывной отдачи», происходящему в реактивном двигателе (ракете). Если рассматривать ракету и выбра­сываемые ею продукты сгорания как единую ме­ханическую систему, то для полу­чения уравнения ее движения можно применить закон сохранения импульса. Эта идея была высказана в 1881 г. Н.И.Кибальчичем и разви­та в трудах К.Э.Циолковского. Уравнение движения тела с переменной массой было выведено в 1897г. И.В.Мещерским.

При выводе уравнения необходимо учитывать, что в процессе движения ракеты изменяется ее масса, т.к. уда­ляются продукты сгорания. Пусть в момент времени t масса ракеты – m и ее скорость - . Через интервал времени dt масса ее уменьшится на dm и станет равной m-dm, а скорость будет равна . Образовавшиеся продукты сгорания топлива за время dt приобрели импульс , где - скорость истечения газа относительно ракеты. Изменение им­пульса всей системы (ракета + продукты сгорания) за время dt равно

Так как - пренебрежимо малая величина, поэтому после сокращений получим . Полагая, что на ракету в далеком космосе не действуют внешние силы, то из закона сохранения импульса следует, что .

Разделим обе части равенства на dt и после простых преобразований получим .

Выражение в правой части равенства имеет размерность силы и называется реактивной си­лой . Таким образом уравнение динамики движения ракеты в космосе можно за­писать в виде: . Интегрируя обе части этого равенства, получим . Постоянную интегрирования С находим из начальных условий : в мо­мент времени t=0 скорость ракеты v=0 и масса m=m₀, тогда и .

Эта формула называется формулой Циолковского. Скорость ракеты v будет тем больше, чем больше масса ракеты и скорость истечения продуктов сго­рания то­плива.

Если на систему действуют внешние силы , то и аналогичным образом плучается уравнение И.В.Мещерского в виде :

2.6. Энергия, работа, мощность. @

Одного понятия импульса оказалось недостаточно для характеристики движения. Например, два снаряда с массами m₁=1кг, m₂=10кг и скоростями v₁=10м/c, v₂=1м/c имеют одинаковые импульс р=10кгм/с, но их разрушающее действие для преграды будет совершенно разное (у первого в 10 раз больше).

Е

Рис.2.6. Прямолиней­ное движение тела под действием силы, направленной под уг­лом к перемещению.

диной мерой различных форм движения и взаимодействия всех видов мате­рии яв­ляется энергия. Различным видам движения и взаимодействия материи, соответствуют различные виды энергии: механическая, те­пловая, химическая, электро-магнитная, атомная.

Простейшей форме движения – меха­нической, соответствует меха­ни­ческая энергия. Она характеризует способность тела или системы тел совершать работу и измеряется количе­ством работы, ко­торую при опре­деленных (заданных) условиях может совершить система. На­пример, катя­щийся шар, сталкиваясь с неко­торым телом, перемещает его, т.е. со­вершает работу. Растянутая пружина, со­кра­ща­ясь после устранения дефор­мирующей силы, совер­шает работу по перемещению своих частей (витков). Следователь­но, катящийся шар и растянутая пружина обла­дают механической энергией. Про­цесс изменения механической энер­гии тела под действием силы называется процес­сом совершения работы. Прираще­ние энергии тела в этом процессе называется работой силы, отсюда следует общее соотношение, связывающее работу и изменение энергии

А=Е₂-Е₁,

где: А – со­вершаемая работа, Е₁ и Е₂ - энергии системы в на­чальном и конечном состояниях.

С

Рис.2.7. Криволинейное движение под действием переменной силы.

ила, приложенная к телу, со­вершает работу, если тело перемещается. Если тело движется прямолинейно и на него дейст­вует постоянная сила, на­правленная под углом  к пере­мещению, то работа равна скалярному произведению векторов перемещения и силы (рис.2.6) ,где - касательная составляющая силы, т.е. проекция на . Если же сила переменна по величи­не и по направ­лению или перемещение не пря­молинейно, то траек­торию движения раз­бивают на малые уча­стки dS - так, чтобы уча­сток можно было бы счи­тать прямоли­нейным и силу, действующей на нем - по­сто­ян­ной (рис.2.7). Тогда работа на этом участке , а работа на всем пути равна сумме всех элемен­тарных работ . При . Для вычисления та­кого интеграла надо знать зависимость от S. Если эту зави­си­мость представить гра­фически (рис.2.8), то­гда ра­бота силы по пе­ремещению из S₁ в S₂ численно равна пло­щади заштрихован­ной фи­гуры, ограни­чен­ной кривой F(S), координатной осью S и двумя вертикаль­ными прямыми S₁ и S₂. Сила не со­вершает работу (А=0), если r=0 или . Если  , то А0; если  , то А0. При одновременном действии на тело нескольких сил, работа равна ал­гебраи­ческой сумме работ состав­ляющих сил .

С

Рис. 2.8. Графическое изображение работы.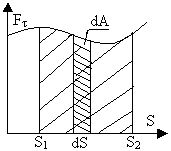

ила F называется консервативной, если совер­шаемая ею работа не за­висит от формы траектории, а зависит от на­чального и конечного поло­жений точки (тела). На рис.2.9. изображены две различ­ные траектории движе­ния тела под действием некоторой консервативной силы. Ра­бота, совершаемая дан­ной силой на пути 1а2 равна А_1а2. Работа, совершаемая на пути 2а1, будет отрица­тельной и А_1а2 = - А_2а1. Поскольку совершаемая работа не зависит от формы траектории, мы можем записать: , или , где - означает интегрирование вдоль замкнутой траектории или интеграл по контуру. Отсюда следует важное свойство консервативных сил - при перемещении материальной точки (тела) вдоль замкнутой траектории работа консервативной силы тожде­ствен­но равна нулю. Сила всемирного тяготения, сила упругости – кон­серва­тивные силы. Силы, неудовлетворяющие этому условию назы­вают неконсервативными или диссипативными. Приме­ром таких сил служат силы трения.

Д

Рис.2.9. Возможные траектории движения тела под действием консервативной силы.

ля характеристики скорости совершения работы вводится понятие мощно­сти. Мощностью, развиваемой силой , называется скалярная физическая величина, численно равная работе, совершаемой этой силой за единицу вре­мени . Если в разные моменты времени dt совершаются разные работы, то используют понятие мгновенной мощности .

Для движущихся тел можно получить формулу мгновенной мощности

или ,

т.е. мощность равна скалярному произведению векторов силы и скорости.

Важное требование, предъявляемое к любому двигателю - это способность совершать большую работу за единицу времени, т.е. иметь большую мощность. Из полученной формулы следует, что для достижения этой цели необходимо либо увеличить силу тяги, развиваемую двигате­лем (например, автомобиля), либо увеличить его быстроходность. Первый путь свя­зан с увеличением силовых нагрузок на все движущиеся части двигателя (поршни, коленчатый вал и т.д.), а они имеют ограниченную прочность. Чтобы де­тали смогли выдерживать действие больших нагрузок, нужно увеличивать их раз­меры, делать их более массивными. Поэтому все мощные тихоходные машины не­обычайно громозд­кие. Второй путь позволяет получить большие мощности при малых силовых нагруз­ках на детали двигателя и меньших его размерах. В совре­менное время этот путь наиболее перспективен.