1 Системы двух линейных уравнений с двумя неизвестными
Системы двух линейных уравнений с двумя неизвестными.
Основные методы решения: подстановка, сложение или вычитание.
Определители второго порядка. Правило Крамера.
Исследование решений системы уравнений.
Системы двух линейных уравнений с двумя неизвестными имеют вид:
где a, b, c, d, e, f – заданные числа; x, y – неизвестные. Числа a, b, d, e – коэффициенты при неизвестных; c, f – свободные члены. Решение этой системы уравнений может быть найдено двумя основными методами.
Метод подстановки.
1) Из одного уравнения выражаем одно из неизвестных, например x, через коэффициенты и другое неизвестное y:
x = ( c – by ) / a . (2)
2) Подставляем во второе уравнение вместо x :
d ( c – by ) / a + ey = f .
3) Решая последнее уравнение, находим y :
y = ( af – cd ) / ( ae – bd ).
4) Подставляем это значение вместо y в выражение (2) :
x = ( ce – bf ) / ( ae – bd ) .
П р и м е р . Решить систему уравнений:
Из первого уравнения выразим х через коэффициенты и y :
x = ( 2y + 4 ) / 3 .
Подставляем это выражение во второе уравнение и находим y :
( 2y + 4 ) / 3 + 3y = 5 , откуда y = 1 .
Теперь находим х, подставляя найденное значение вместо y в
выражение для х: x = ( 2 · 1 + 4 ) / 3, откуда x = 2 .
Сложение или вычитание. Этот метод состоит в следующем.
1) Умножаем обе части 1-го уравнения системы (1) на (– d ), а обе части 2-го уравнения на а и складываем их:
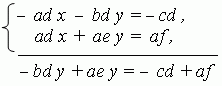
Отсюда получаем: y = ( af – cd ) / ( ae – bd ).
2) Подставляем найденное для y значение в любое уравнение системы (1):
ax + b( af – cd ) / ( ae – bd ) = c.
3) Находим другое неизвестное: x = ( ce – bf ) / ( ae – bd ).
П р и м е р . Решить систему уравнений:
методом сложения или вычитания.
Умножаем первое уравнение на –1, второе – на 3 и складываем их:
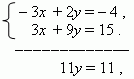
отсюда y = 1. Подставляем это значение во второе уравнение
(а в первое можно?): 3x + 9 = 15, отсюда x = 2.
Определители второго порядка. Мы видели, что формулы для решения системы двух линейных уравнений с двумя неизвестными имеют вид:
x = ( ce – bf ) / ( ae – bd ) ,
(3)
y = ( af – cd ) / ( ae – bd ) .
Эти формулы легко запоминаются, если ввести для их числителей и знаменателей следующий символ:
, который
будет обозначать выражение: ps – qr .
Это выражение получается перекрёстным умножением чисел p, q, r, s :
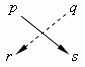
и последующим вычитанием одного произведения из другого: ps – qr. Знак « + » берётся для произведения чисел, лежащих на диагонали, идущей из левого верхнего числа к правому нижнему; знак « – » - для другой диагонали, идущей из правого верхнего числа к левому нижнему. Например,
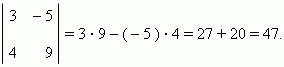Выражение
называется определителем
второго порядка.
Правило Крамера. Используя определители, можно переписать формулы (3):
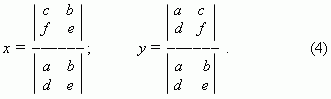
Формулы (4) называются правилом Крамера для системы двух линейных уравнений с двумя неизвестными.
П р и м е р . Решить систему уравнений
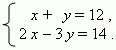
используя правило Крамера.
Р е ш е н и е . Здесь a = 1, b = 1, c = 12, d = 2, e = –3, f = 14 .
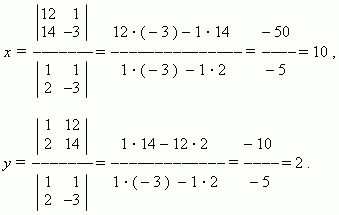
Исследование решений системы двух линейных уравнений с двумя неизвестными, показывает, что в зависимости от коэффициентовуравнений возможны три различных случая:
1) коэффициенты при неизвестных не пропорциональны: a : d ≠ b : e ,
в этом случае система линейных уравнений имеет единственное решение, получаемое по формулам (4);
2) все коэффициенты уравнений пропорциональны: a : d = b : e = c : f ,
в этом случае система линейных уравнений имеет бесконечное множество решений, так как здесь мы имеем фактически одноуравнение вместо двух.
П р и м е р . В системе уравнений
и эта система уравнений имеет бесконечное множество решений.
Разделив первое уравнение на 2, а второе – на 3, мы получим два
одинаковых уравнения:
т.е. фактически одно уравнение с двумя неизвестными, у которого
бесконечное множество решений.
3) коэффициенты при неизвестных пропорциональны, но не пропорциональны свободным членам: a: d = b: e ≠ c: f,
в этом случае система линейных уравнений не имеет решений, так как мы имеем противоречивые уравнения.
П р и м е р . В системе уравнений
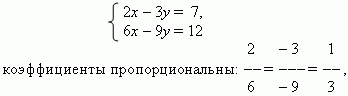
но отношение свободных членов 7 / 12 не равно 1 / 3.
Почему эта система не имеет решений? Ответ очень простой.
Разделив второе уравнение на 3, мы получим:
Уравнения этой системы противоречивы, потому что одно и то
же выражение 2x – 3y не может быть одновременно равно и 7, и 4.
2 Совместные и несовместные системы
это система в которой найдя одно неизвестное из любого уравнения.... подставляют его в другое... получается выражение оставшегося неизвестного через другое.... подставляется в третье уравнение...находиться второе неизвестное.... ну и потом логическим путем третье
Пример 1
Решить
систему линейных уравнений
Что сразу бросается в глаза в этой системе? Количество уравнений – меньше, чем количество переменных. Если количество уравнений меньше, чем количество переменных, то сразу можно сказать, что система либо несовместна, либо имеет бесконечно много решений. И это осталось только выяснить.
Начало решения совершенно обычное – запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
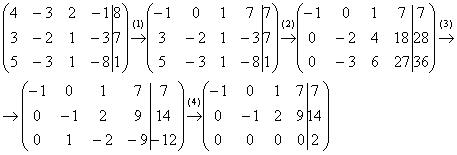
(1) На левой верхней ступеньке нам нужно получить +1 или –1. Таких чисел в первом столбце нет, поэтому перестановка строк ничего не даст. Единицу придется организовать самостоятельно, и сделать это можно несколькими способами. Я поступил так: К первой строке прибавляем третью строку, умноженную на –1.
(2) Теперь получаем два нуля в первом столбце. Ко второй строке прибавляем первую строку, умноженную на 3. К третьей строке прибавляем первую строку, умноженную на 5.
(3) После выполненного преобразования всегда целесообразно посмотреть, а нельзя ли упростить полученные строки? Можно. Вторую строку делим на 2, заодно получая нужную –1 на второй ступеньке. Третью строку делим на –3.
(4) К третьей строке прибавляем вторую строку.
Наверное,
все обратили внимание на нехорошую
строку, которая получилась в результате
элементарных преобразований: 
.
Ясно, что так быть не может. Действительно,
перепишем полученную матрицу 
обратно
в систему линейных уравнений: 
Если
в результате элементарных преобразований
получена строка вида 
,
где 
–
число, отличное от нуля, то система
несовместна (не имеет решений).
Как
записать концовку задания? Необходимо
записать фразу «в результате элементарных
преобразований получена строка вида
,
где 
»
и дать ответ: система не имеет решений
(несовместна).
Обратите внимание, что нет никакого обратного хода алгоритма Гаусса, решений нет и находить попросту нечего.