Геометрический смысл производной

Ключевые слова: геометрический смысл производной

Геометрический смысл производной. Производная в точке x ₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

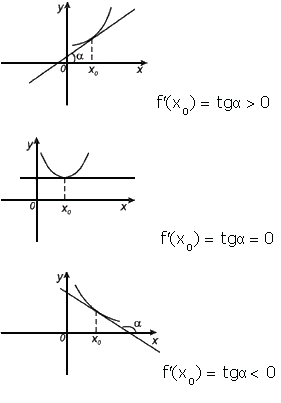
Рассмотрим график функции y = f ( x ):

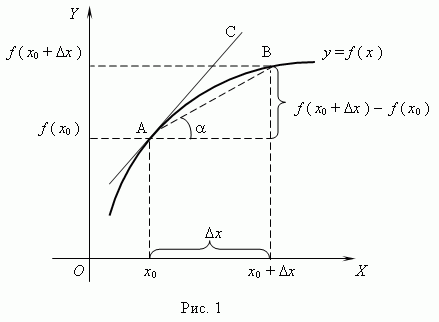
Из рис.1 видно, что для любых двух точек A и B графика функции:  xf(x0+ x)−f(x0)=tg , где   - угол наклона секущей AB.  Таким образом, разностное отношение равно угловому коэффициенту секущей.  Если зафиксировать точку A и двигать по направлению к ней точку B, то  x неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС.  Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует:

производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.

В этом и состоит геометрический смысл производной.

45

Дифференциал

        Определение 4.3   Пусть дана функция  , и   -- внутренняя точка её области определения. Придадим аргументу приращение   и рассмотрим приращение функции

Если это приращение   можно представить в виде

где величина   не зависит от приращения  , а   -- бесконечно малая при базе   величина, имеющая больший порядок малости, чем  , то произведение   называется дифференциалом функции   в точке   и обозначается   или просто  .     

Таким образом, дифференциал   -- это функция двух аргументов   и  , причём от переменного приращения   дифференциал зависит линейно ( входит в выражение, задающее  , как множитель, стоящий в первой степени). Заметим, что в формуле

второе слагаемое в правой части имеет порядок малости, больший, чем у  , и, следовательно, при   больший, чем у  . Поэтому дифференциал   -- это главная, линейная по  , часть приращения функции.

        Теорема 4.3   Функция   имеет дифференциал   в точке   тогда и только тогда, когда она имеет производную   в этой точке; при этом

Введение в цифровую электронику

        Доказательство.     Пусть функция   имеет дифференциал, то есть её приращение можно представить в виде  . Разделим обе части равенства на  :

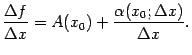
При   в правой части предел первого слагаемого равен  , поскольку эта величина не зависит от   и, следовательно, при вычислении предела считается постоянной. Далее,

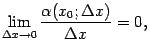
так как, по определению дифференциала,   имеет более высокий порядок малости, нежели  . Значит, существует предел

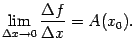
Но этот предел, по определению, равен производной  . Значит, функция имеет производную в точке  , и  , откуда

46

47 В блокноте

48

Уравнение касательной

Пусть функция задается уравнением y=f(x), нужно написать уравнение касательной в точке x0. Из определения производной: 

y/(x)=limΔx→0ΔyΔx

Δy=f(x+Δx)−f(x). 

Уравнение касательной к графику функции: y=kx+b (k,b=const). Из геометрического смысла производной: f/(x0)=tgα=k Т.к. x0 и f(x0)∈  прямой, то уравнение касательной записывается в виде: y−f(x0)=f/(x0)(x−x0) , или

y=f/(x0)·x+f(x0)−f/(x0)·x0. 

 

 

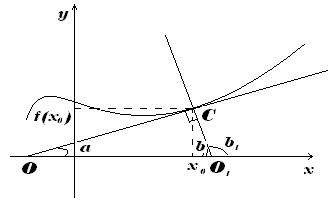
Уравнение нормали

Нормаль -- это перпендикуляр к касательной (см. рисунок). Исходя из этого:

tgβ=tg(2π−α)=ctgα=1tgα=1f/(x0)

Т.к. угол наклона нормали -- это угол β1, то имеем:

tgβ1=tg(π−β)=−tgβ=−1f/(x).

Точка (x0,f(x0))∈  нормали, уравнение примет вид:

y−f(x0)=−1f/(x0)(x−x0).

49

49

роизводная сложной функции

"Двухслойная" сложная функция записывается в виде где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f.  Если f и g - дифференцируемые функции, то сложная функция   также дифференцируема по x и ее производная равна Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)!  Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга.  Рассмотрим несколько примеров, иллюстрирующих правило производной сложной функции. Это правило широко применяется и во многих других задачах раздела "Дифференцирование".

И в тетради

50

Пусть задана зависимость двух переменных   и   от параметра  , изменяющегося в пределах от   до  :

Пусть функция   имеет обратную:  . Тогда мы можем, взяв композицию функций   и  , получить зависимость   от  :  . Зависимость величины   от величины  , заданная через зависимость каждой из них от параметра   в виде  , называется функцией  , заданной параметрически.

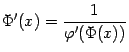Производную функции  , заданной параметрически, можно выразить через производные функций   и  : поскольку   и, по формуле производной обратной функции,  , то

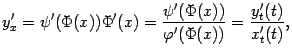
где   -- значение параметра, при котором получается интересующее нас при вычислении производной значение  .

Заметим, что применение формулы приводит нас к зависимости между   и  , снова выраженной в виде параметрической зависимости:  ,  ; второе из этих соотношений -- то же, что участвовало в параметрическом задании функции  . Несмотря на то, что производная не выражена через   в явном виде, это не мешает решать нам задачи, связанные с нахождением производной, найдя соответствующее значение параметра  . Покажем это на следующем примере.