Свойства
Ограниченность.
Всякая неубывающая последовательность ограничена снизу.
Всякая невозрастающая последовательность ограничена сверху.
Всякая монотонная последовательность ограничена по крайней мере с одной стороны.
Монотонная последовательность сходится тогда и только тогда, когда она ограничена с обеих сторон.(Теорема Вейерштрасса об ограниченных монотонных последовательностях)
Сходящаяся неубывающая последовательность ограничена сверху своим пределом.
Сходящаяся невозрастающая последовательность ограничена снизу своим пределом.
Ограниченная последовательность. Последовательность (чисел, точек и т.п.), члены которой образуют ограниченное множество, называется ограниченной. Аналогично последовательность называется ограниченной сверху (снизу), если ее члены образуют ограниченное сверху (снизу) множество (см. также Верхняя грань).
39
Предел последовательности
[править]
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Предел.
В математике пределом последовательности элементов пространства называют элемент того же пространства, который обладает свойством «притягивать», в некотором смысле, элементы данной последовательности. Свойство последовательности, иметь или не иметь предел, называют сходимостью: если у последовательности есть предел, то говорят, что данная последовательность сходится, в противном случае (если у последовательности нет предела) говорят, что последовательность расходится. Часто встречающимся является предел числовой последовательности.
Пределом последовательности точек топологического пространства является такая точка, каждая окрестность которой содержит все элементы последовательности, начиная с некоторого номера. Все открытые, в смысле данной топологии, множества, содержащие данную точку, образуют систему окрестностей этой точки. В метрическом пространстве систему окрестностей образуют, например, все открытые шары с центром в данной точке. Поэтому свойство сходимости последовательности элементов метрического пространства к данной точке формулируется как способность «удерживать» на заданном расстоянии все точки последовательности, начиная с некоторого номера.
Сходящиеся последовательности обладают следующим свойством: каждая подпоследовательность сходящейся последовательности сходится, и её предел совпадает с пределом исходной последовательности. Другими словами, у последовательности не может быть двух различных пределов.[1] Может, однако, оказаться, что у последовательности нет предела, но существует подпоследовательность (данной последовательности), которая предел имеет. Если из последовательности точек пространства можно выделить сходящуюся подпоследовательность, то, говорят, что данное пространство компактно или, точнее, секвенциально компактно.
Понятие предела последовательности непосредственно связано с понятием предельной точки (множества): если у множества есть предельная точка, то существует последовательность элементов данного множества, сходящаяся к данной точке. Таким образом, у последовательности может быть несколько предельных точек, но, если последовательность сходится, то все предельные точки совпадают друг с другом и совпадают с пределом самой последовательности.
Предел числовой последовательности является основным объектом рассмотрения в математическом анализе. В общей топологии рассматриваются наиболее общие свойства сходимости, а, также, вводятся и изучаются обобщения.
40
усть функция f(x) определена в некоторой проколотой окрестности точки x0 .
Число A называется пределом функции f(x) при x → x0 (или в точке x0), если для любого ε > 0 найдется δ > 0 такое, что для всех x, для которых 0 < |x − x0| < δ, справедливо неравенство |f(x) − A| < ε, т.е.
lim |
x → x0 |
f(x) = A ε > 0 δ > 0 : 0 < |x − x0| < δ |f(x) − A| < ε.
Используем понятие окрестности и учтем, что
0 < |x − x0| < δ x
· |
O |
δ (x0 ) и |f(x) − A| < ε f(x) Oε (A).
(Точка над символом окрестности указывает, что это проколотая окрестность.)
Теперь определение предела функции в точке можно представить в виде
|
f(x) = A ε > 0 δ > 0 : x
δ (x0 ) f(x) Oε (A). |
|
Еше проще:
|
f(x) = A O (A)
(x0) : x
(x0) f(x) O (A). |
|
Геометрический смысл того, что x
· |
O |
(x0) f(x) O (A) поясняет рис.1
На этом рисунке проколотая окрестность
· |
O |
(x0) точки x0 изображена красным отрезком на оси OX из которого исключена точка x0. Окрестность O (A) точки Aизображена розовым отрезком на оси OY. Очевидно, что образ окрестности
· |
O |
(x0) при отображении y = f(x) содержится в O (A).
Пределы суммы, произведения и частного двух функций
Теорема 1. Если существуют
lim |
x → x0 |
f(x) = A и
lim |
x → x0 |
g(x ) = B, то существуют пределы
[f(x) ± g(x) ] = A ± B;
[ f(x) · g(x) ] = A · B;
=
, (B ≠ 0). |
Доказательство приведено в книге Я.С. Бугрова и С.М. Никольского “Дифференциальное и интегральное исчисление”. М.: ФИЗМАТЛИТ, 1980. Стр. 84.
Теорема 2 (о переходе к пределу в неравенстве). Если x
· |
O |
(x0) f(x) ≤ g(x) и существуют пределы
lim |
x → x0 |
f(x) и
lim |
x → x0 |
g(x) , то
lim |
x → x0 |
f(x) ≤
lim |
x → x0 |
g(x) .
Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 44.
Замечание. Строгое неравенство f(x)<g(x) при переходе к пределу может перейти в равенство.
Теорема 3 (о пределе промежуточной функции). Если x
· |
O |
(x0) u(x) ≤ f(x) ≤ v(x) и
lim |
x → x0 |
u(x) =
lim |
x → x0 |
v (x) = A, то
lim |
x → x0 |
f(x) = A.
Доказательство приведено в книге И.М. Петрушко и Л.А. Кузнецова “Курс высшей математики: Введение в математический анализ. Дифференциальное исчисление.” М.: Изд–во МЭИ, 2000. Стр. 45.
Односторонние пределы
Пусть функция f(x) определена на интервале (x0, x1).
Число A называется пределом функции f(x) справа, в точке x0 если для любого ε > 0 найдется δ > 0 такое, что для всех x, для которых x0 < x < x0 + δ , справедливо неравенство | f(x) − A | < ε, т.е.
|
f(x) = A ε > 0 δ > 0 : x0 < x < x0 + δ | f(x) − A | < ε. |
|
Предел функции f(x) в точке x0 справа обозначается символом f(x0 + 0)
Число A называется пределом функции f(x) слева, в точке x1 если для любого ε > 0 найдется δ > 0 такое, что для всех x, для которых x1 − δ < x < x1 , справедливо неравенство | f(x) − A | < ε, т.е.
|
f(x) = A ε > 0 δ > 0 : x1 − δ < x < x1 | f(x) − A | < ε. |
|
Предел функции f(x) в точке x1 слева обозначается символом f(x1 − 0)
Теорема 4. Для того чтобы существовал предел
lim |
x → a |
f(x) , равный A, необходимо и достаточно, чтобы существовали и были равны A оба односторонних предела
lim |
x → a − 0 |
f(x) и
lim |
x → a + 0 |
f(x) .
Функция f(x) называется ограниченной в точке x0, если существуют число M > 0 и окрестность O(x0), такие что x O(x0) | f(x) | < M .
Теорема 5. Если функция f(x) определена в некоторой окрестности точки x0 и имеет в точке x0 односторонние пределы, то она ограничена в этой точке.
Доказательство приведено в книге Я.С. Бугрова и С.М. Никольского “Дифференциальное и интегральное исчисление”. М.: ФИЗМАТЛИТ, 2002. Стр. 81.
Функция f(x) называется бесконечно большой при x → x0, если
|
M > 0
(x0) : x
(x0) | f(x) | > M. |
|
В этом случае принято говорить, что предел функции бесконечен, и записывать этот факт в виде
|
f(x) = ∞. |
|
Прямая x = x0 называется вертикальной асимптотой графика функции y = f(x), если хотя бы один из односторонних пределов f(x0 + 0) и f( x0 − 0) равен + ∞ или−∞.
Некоторые (не не все!) примеры поведения графика функции y = f(x) вблизи вертикальной асимптоты x = x0 изображены на рис. 2.
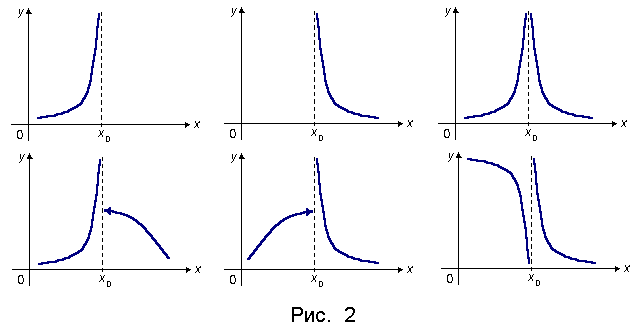
41
ОДНОСТОРОННИЙ ПРЕДЕЛ
Перевод
ОДНОСТОРОННИЙ ПРЕДЕЛ
-
предел функции в нек-рой точке справа
или слева. Пусть f - отображение
упорядоченного множества X(напр.,
множества, лежащего на числовой прямой),
рассматриваемого как топологич.
пространство с топологией, порожденной
отношением порядка, в топологич.
пространство Y и 
.
Предел отображения f по любому
интервалу 
наз.
пределом слева отображения f и обозначают
(он
не зависит от выбора 
),
а предел по интервалу 
наз.
пределом справа и обозначают
(он
не зависит от выбора 
).
Если точка 
является
предельной как слева, так и справа для
множества определения функции f, то
обычный предел
по проколотой окрестности точки х 0 (в этом случае его наз. также двусторонним, в отличие от односторонних пределов) существует тогда и только тогда, когда в точке х 0 существуют пределы слева и справа и они равны между собой.
42