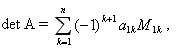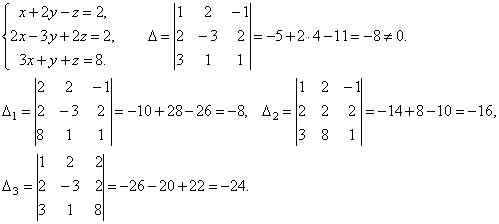3 Определители матриц, способ № 1:

Определителем квадратной матрицы (det A) называется число, которое может быть вычислено по элементам матрицы по формуле:

Свойства определителей

1. Определитель не меняется при транспонировании.

2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.

3. Если в определителе переставить две строки, определитель поменяет знак.

4. Определитель, содержащий две одинаковые строки, равен нулю.

5. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k.

6. Определитель, содержащий две пропорциональные строки, равен нулю.

7. Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых a_{i j} = b_j + c_j (j= ), то определитель равен сумме определителей, у которых все строки, кроме i-ой, - такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов b_j, в другом - из элементов c_j.

8. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число.

Определитель первого порядка равен тому единственному элементу, из которого состоит соответствующая матрица.

Определитель второго порядка вычислим, например, по элементам первой строки

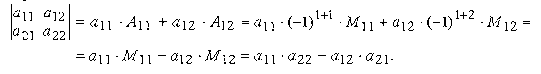
Запишем разложение данного определителя по элементам второй строки

Полученный результат совпадает с результатом вычисления определителя по первой строке. Этот же результат получится и при разложении по любому из столбцов. Рекомендуем это проверить самостоятельно.

Из сказанного можно заключить, что определитель второго порядка равен произведению элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной диагонали.

Найдем определитель третьего порядка, раскладывая его по элементам, например, третьего столбца

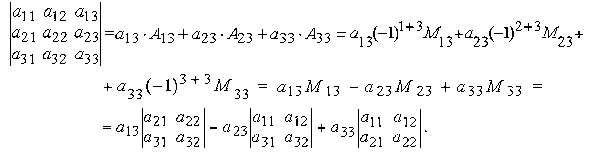
Пример.

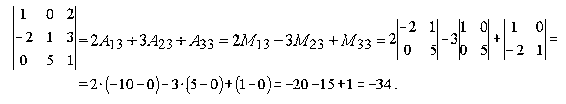
Таким образом, вычисление определителя третьего порядка сводится к вычислению определителей второго порядка.

Получается, что определитель n - го порядка мы найдем через определители (n -1) - го порядка.

4

5 Правило крамера

Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:

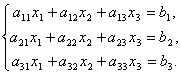
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы.

Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов

Тогда можно доказать следующий результат.

Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём

Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A₁₁ элемента a₁₁, 2-ое уравнение – на A₂₁ и 3-е – на A₃₁:

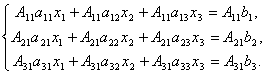
Сложим эти уравнения:

Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца

.

Далее рассмотрим коэффициенты при x₂:

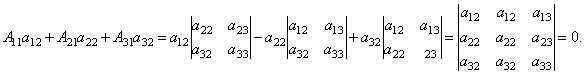
Аналогично можно показать, что и  .

Наконец несложно заметить, что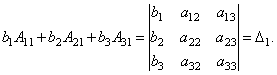 

Таким образом, получаем равенство:  .

Следовательно,  .

Аналогично выводятся равенства   и  , откуда и следует утверждение теоремы.

Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.

Примеры. Решить систему уравнений

1. 

Итак, х=1, у=2, z=3.

2. Решите систему уравнений при различных значениях параметра p: 

Система имеет единственное решение, если Δ ≠ 0.

. Поэтому  .

1. При 

2. При p = 30 получаем систему уравнений 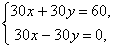  которая не имеет решений.

3. При p = –30 система принимает вид 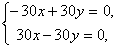  и, следовательно, имеет бесконечное множество решений x=y, yR.

МЕТОД ГАУССА

6

7 Однородная система уравнений

8

9

Определение 1. Величина, полностью характеризуемая своим числовым значением в выбранной системе единиц, называется скалярной или скаляром.

(Масса тела, объем, время и т.д.)

Определение 2. Величина, характеризуемая числовым значением и направлением, называется векторной или вектором.

Определение 3. Модуль вектора – это длина отрезка AB.

Определение 4. Вектор, модуль которого равен нулю, называется нулевым, обозначается  .

Определение 5. Векторы, расположенные на параллельных прямых или на одной прямой называются коллинеарными. Если два коллинеарных вектора имеют одинаковое направление, то они называются сонаправленными.

Определение 6. Два вектора считаются равными, если они сонаправлены и равны по модулю.

10

Умножение вектора на число.

Опр. 10. Произведением вектора    на скаляр k называется вектор

 = k  =  k,

имеющий длину ka, и направление, которого:

1.     совпадает с направлением вектора  , если k > 0;

2.     противоположно направлению вектора  , если k < 0;

3.     произвольно, если k = 0.

Свойства умножения вектора на число.

1^о. (k + l)  = k  + l .

 k(  +  ) = k  + k .

2^o. k(l ) = (kl) .

3^o. 1  =  , (–1)   = –  , 0   =  .

11

Свойства векторов.

Опр. 11. Два вектора   и   называются коллинеарными, если они расположены на параллельных прямых или на одной прямой.

Нулевой вектор   коллинеарен любому вектору.

Теорема 1. Два ненулевых вектора    и  коллинеарны,  когда они пропорциональны т.е.

 = k , k – скаляр.

Опр. 12. Три вектора  ,  ,   называются компланарными, если они параллельны некоторой плоскости или лежат в ней.

12