4. 3. Гармонический осциллятор. Примеры гармонических осцилляторов. @

Тела, которые при движении совершают гармонические ко­лебания, называют гармоническими осциляторами. Рассмотрим ряд примеров гармонических осциляторов.

Пример1. Пружинный маятник – это тело массой m, способное совершать колебания под действием силы упругости невесомой (m_{пружины}m_тела) пружины (рис.4.2).

Т

Рис.4.3. Физический маятник.

рением в системе пренебрегаем. При смещении тела на расстояние х от положе­ния равновесия О на него дейст­вует сила уп­ругости пружины, направленная к положению равновесия: , где k - коэффициент упругости (жесткости) пружины. По второму закону Ньютона . От­сюда и, если обозначить , тогда получим дифференциальное урав­нение гармонических колебаний. Его решения имеют вид либо . Таким образом, колебания пружинного маятника - гармонические с циклической час­тотой и периодом .

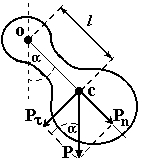
Пример 2. Физический маятник - это твердое тело, совер­шаю­щее колебания под действием силы тяжести вокруг подвижной го­ризон­тальной оси, не совпадающей с его цен­тром тяжести С (рис. 4. 3). Ось проходит через точку О. Если маятник откло­нить от положения равновесия на малый угол  и отпус­тить, он будет совершать ко­лебания, следуя основному уравнению динамики вращательного движения твердого тела , где J - момент инерции маятника относительно оси, М ‑ момент силы, возвращающей физический маятник в поло­жение равно­весия. Он создается силой тяжести , ее момент равен (l=ОС). В результате получаем  .      Это дифференциальное уравнение колебаний для произвольных углов отклонения. При малых углах, когда , или, принимая , получим дифференциальное уравнение колебания физического маятника . Его решения имеют вид или . Таким образом, при малых отклонениях от положения равновесия физический маят­ник совершает гармонические колебания с циклической частотой и периодом .

Пример3. Математический маятник - это материальная точка с массой m (тяжелый шарик малых размеров), подвешенная на невесомой (по сравнению с m шарика), уп­ругой, нерастяжимой нити длинною l. Если вывести шарик из положения равновесия, отклонив его от вертикали на небольшой угол , а затем отпустить, он будет совершать колебания. Если рассматривать данную систему как физический маятник с моментом инерции материальной точки J = ml², то из формул для физического маятника получим выражения для циклической частоты и периода колебаний математического маятника

, .

4. 4. Затухающие колебания. @

В рассмотренных примерах гармонических колебаний единственной силой, действующей на материальную точку (тело), была квазиупругая сила F и не учитывались силы сопротивления, которые присутству­ют в лю­бой реальной системе. Поэтому рассмотренные колебания можно назвать идеальными незатухающими гармоническими колебаниями.

Наличие в реальной колебательной системе силы сопротивления среды при­во­дит к уменьшению энергии системы. Если убыль энергии не пополнять за счет работы внешних сил, колебания будут затухать. Затухающими называются колеба­ния с уменьшающейся во времени амплитудой.

Рассмотрим свободные затухающие колебания. При небольших скоростях сила сопротивления F_C пропорциональна скорости v и обратно пропорциональна ей по направлению , где r - коэффициент сопротивления среды. Используя второй закон Ньютона, получим дифференциальное уравнение затухающих колебаний , ,  . Обозначим , . Тогда дифференциальное уравнение приобретает вид:

Рис.4.4. Зависимость смеще­ния и амплитуды затухаю­щих колебаний от времени.

.

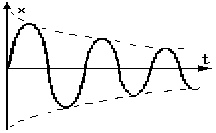
Это дифференциальное уравнение затухающих колебаний. Здесь ₀ - собственная частота колеба­ний системы, т.е. частота свободных колебаний при r=0,  - коэффициент зату­хания оп­ределяет скорость убывания амплитуды. Решениями этого уравнения при условии ₀ являются

 либо .

График последней функции представлен на рис.4.4. Верхняя пунктирная линия дает график функции , А₀ - амплитуда в начальный момент времени. Амплитуда во времени убывает по экспоненциальному закону,  - коэффициент зату­хания по величине обратен времени релакса­ции , т.е. вре­мени за которое амплитуда уменьшается в e раз, так как

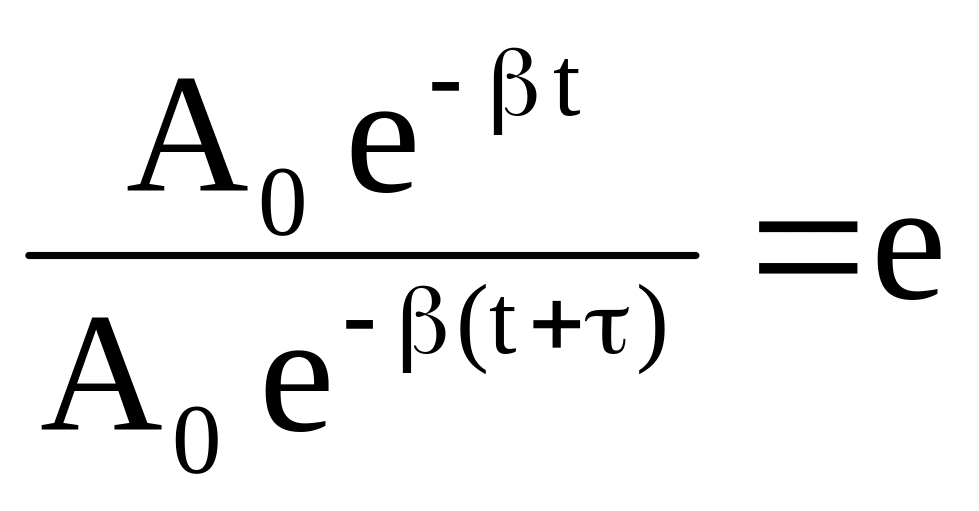, ,  = 1, . Частота и период затухающих колебаний , ; при очень малом сопротивлении среды (²₀²) период колебаний практически ра­вен . С ростом  период колебаний увеличивается и при >₀ решение дифференциального уравнения показывает, что колебания не совершаются, а происходит монотонное движение системы к положению равновесия. Такое движение называют апериодическим.

Для характеристики скорости затухания колебаний служат еще два параметра : декремент затухания D и логарифмический декремент . Декремент затуха­ния показывает во сколько раз уменьшается амплитуда колебаний за время од­ного периода Т.

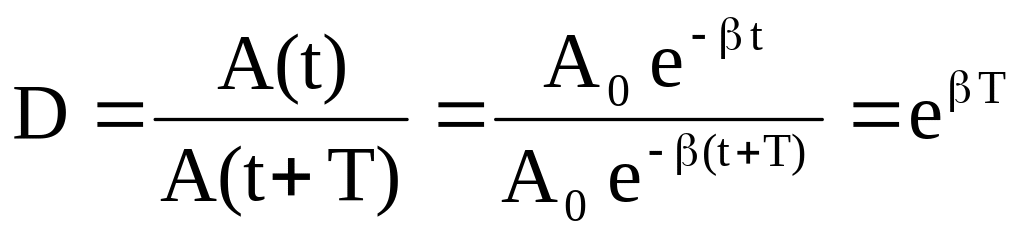
Н

Рис.4.5. Вид резонансных кривых.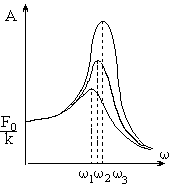

атуральный логарифм от декремента затухания есть логарифмический декремент 

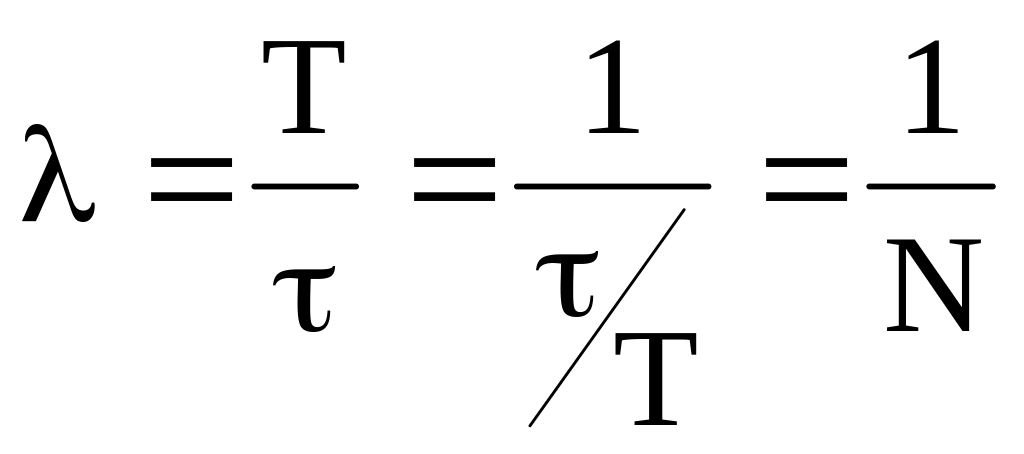. Так как , то , где N - число колебаний за время .