Разложение булевых функций по переменным

Введем обозначение:

0 0	1
0 1	0
1 0	0
1 1	1

Теорема: Каждую функцию алгебры логики можно представить в виде:

, где дизъюнкция берется по всевозможным наборам .

5)Если в конъюнкцию не входит переменная , то нужно рассмотреть равносильное выражение и вновь перейти к шагу 2.

6) Если появились одинаковые конъюнкции вновь перейти к шагу 3.

Пример:

1)

2)

Опред. Выражение вида

Называется СКНФ

1)

000	0
001	1
010	1
011	0
100	0
101	1
110	1
111	0

Каждое из выражений называется элементарной конъюнкцией.

СДНФ называется совершенной, так как каждое слагаемое содержит все переменные;

дизъюнктивной, так как главная операция-дизъюнкция;

нормальной, так как совершенный вид такой формы является однозначным способом записи формулы, реализующей заданную функцию.

1. Табличный способ построения СДНФ

000	0
001	1
010	1
011	0
100	0
101	1
110	0
111	0

2. Аналитический способ построения СДНФ

1) Преобразуем формулу так, что бы в ней были только , причем могут стоять только над переменными

2) Используя законы дистрибутивности, преобразуем формулу так, чтобы выполнялись раньше, чем .

3) Если в ДНФ имеется несколько одинаковых конъюнкций, то оставляем лишь одну.

4) Делаем все конъюнкции правильными

Упражнения: построить СДНФ и СКНФ

1)

2)

Полином Жегалкина

Теорема:

Всякую булеву функцию можно представить в виде:

, где сумма по берется по всем наборам, где

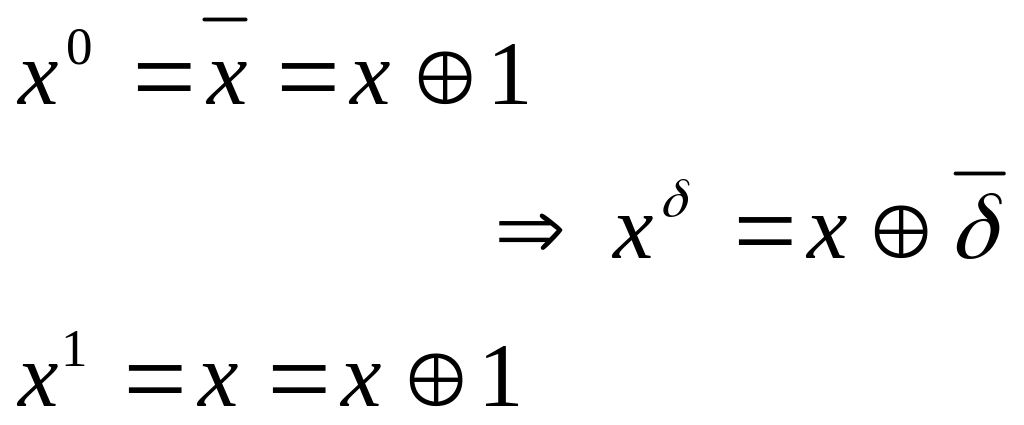
Подставим вместо выражение , раскрыв скобки по закону дистрибутивности и приведя подобные члены по правилу , придем к представлению в виде:

,

где коэффициенты или .

Это представление носит название полинома Жегалкина.

2.

3. Чтобы построить СКНФ для некоторой функции, надо построить отрицание в СДНФ, то есть взять дизъюнкцию элем. конъюнкций, дающих значение 0 и взять отрицание от .

Пример:

000	0
001	1
010	1
011	0
100	0
101	1
110	1
111	0

2) Метод неопределенных коэффициентов

00	1
01	1
10	0
11	1

Опред.: Если ПЖ не содержит конъюнкций, то есть имеет вид , то соответствующая ему функция называется линейной.

Упражнения

Построить ПЖ

1)

2)

3)

Теорема: Всякая булева функция может быть представлена в виде полинома Жегалкина единственным образом.

Если у функции есть фиктивные переменные, то они н6е должны входить в ПЖ.

Способы нахождения ПЖ:

1) С помощью законов алгебры логики

а) из исходной формулы

б) из СДНФ

Следствие:

Полными являются системы:

Доказательство:

а)

б)

Доказать самостоятельно: полные системы

Замыкание

Опред.: Пусть некоторый класс (подмножество) булевых функций .

Замыканием называется множество всех булевых функций, представимых в виде суперпозиции функций из .

1)

2)

множество всех линейных функций

Полнота и замкнутость

Опред.: Система функций называется функционально полной, если любая булева функция может быть представлена в виде суперпозиции функций этой системы.

Пример: 1) полная

2) полная

Доказательство:

Если , то

Если , то её можно представить в виде СДНФ

3) неполная

Теорема о полноте второй системы булевых функций

Пусть даны 2 системы и , причем 1 – полная и каждая функция системы (1) выражается в виде суперпозиции функций системы (2).

В этом случае система (2) является полной (без доказательства).

2) Класс класс функций, сохраняющих константу «1», то есть

Примеры:

Теорема замкнутый класс (доказать самостоятельно)

3) Класс класс самодвойственных функций, то есть

Примеры:

Так как самодвойственная функция на противоположных наборах принимает противоположные значения, то самодвойственные функции определяются своими значениями полностью на первой половине строк

Теорема: замкнутый класс

где

Свойства замыкания

1)

2)

3)

4)

Опред.: Класс называется функционально замкнутым, если

1) замкнут

2) не замкнут

3) замкнут

Важнейшие замкнутые классы

1. Класс класс функций, сохраняющих константу 0, то есть

Пример:

Теорема: замкнутый класс

Функцию , где

2. 

000	0
001	0
010	0
011	1
100	0
101	1
110	1
111	0

3. 

4. Класс класс монотонных функций

Введем обозначение:

наборы значений переменной

значение функции на этих наборах

Опред.: Наборы и находятся в отношении предшествования ,

если

несравнимы

Опред.: Булева функция называется монотонной, если и таких, что выполняется неравенство