4.4. Распределение соединений по слоям

Межслойный переход; расслоение; охватывающий прямоугольник; граф несовмести­мости; совмещенная топология; бихроматический подграф; ортогональная трассировка

После определения планарности, в том случае когда ММ КС непланарна, решают задачу распределения ребер графа или гиперграфа (соединений КС) по слоям. Целью при ее решении является наиболее эффективное использование площади КП при одновременной оптимизации таких конструктивных парамет­ров КС, как число слоев, межслойных переходов, процент реализо­ванных соединений.

В зависимости от организации процесса трассировки расслоение осуществляется либо до, либо после, либо в процессе трассировки.

Основная идея алгоритмов расслоения, работающих до трасси­ровки, заключается в априорном выделении в КС по тем или иным признакам конфликтующих групп соединений, которые ввиду неизбежных пересечений невозможно назначить на один слой.

Часто используемым методом расслоения до трассировки является простой алгоритм формирования двух подмножеств соединений, распределяемых в ортогональной системе координат в двух слоях. Подмножества вертикальных и горизонтальных отрезков назначаются в различные слои. Решение получается быстро, однако очевидно, что оно не оптимально с точки зрения требуемой площади трассировки и числа межслойных переходов (рис. 4.14).

В [59] предлагается задавать меру «взаимодействия» соедине­ний при решении задачи расслоения путем построения для каждой цепи е_i охватывающего прямоугольника Пi Считается при этом, что две цепи перекрываются, если . Далее строится граф перекрытий G_p = (E, U), где множество вершин Е соответствует цепям, а ребра u принадлежащее U—перекрытиям между ними.

Очевидно, что хроматическое число у_р графа G_p = (E, U) служит верхней оценкой числа слоев, необходимых для реализации всех соединений КС. Величину у_р называют степенью перекрытия системы подмножеств е_i. Очевидно, все связывающие деревья для e_i могут быть назначены на один слой, когда у_р=1.

Рассмотрим пример построения охватывающих прямоугольни­ков для G-цепей (рис. 4.15). Для указанного примера легко построить граф перекрытий G_p (рис. 4.16). Согласно алгоритму (см. 1.3) можно раскрасить граф G_p в два цвета (I и II на рис. 4.16). Тогда получаем у_р=2. Иными словами, схема может быть реализована в двух слоях и содержит два непересекающихся

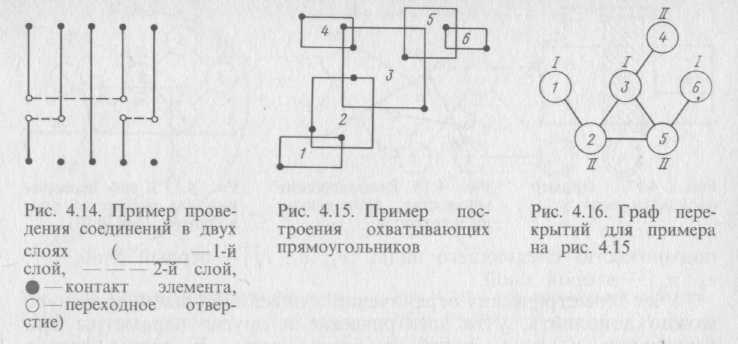
подмножества следующего вида: {е₁, е₃, е₆} — первый слой; {е₂, е₅, е₄)—второй слой.

Учет геометрических ограничений в описанной выше процедуре можно дополнить, учтя электрические и другие параметры при реализации е_i и е_j цепей в одном слое. В таком случае подсчитывается аддитивная функция вида

где aij — эвристические весовые коэффициенты; p_ij — учитываемые параметры цепей.

Здесь, как и в предыдущем случае, строится граф несовмести­мости G_p = (E, U), однако каждому uij принадлежащему U теперь присваивается вес F_ij Задача расслоения сводится к построению такой раскраски графа в у цветов, чтобы сумма весов ребер, соединяющих вершины одного цвета, была минимальной. При этом раскраска возможна одним из известных алгоритмов, описанных в 1.2.

Отметим, что степень влияния е_i на е_j можно оценивать как число путей минимальной длины для проведения соединения ej через Пj. На рис. 4.17 показано, как запрещенная (заштрихован­ная) область препятствует оптимальной реализации цепи е_j

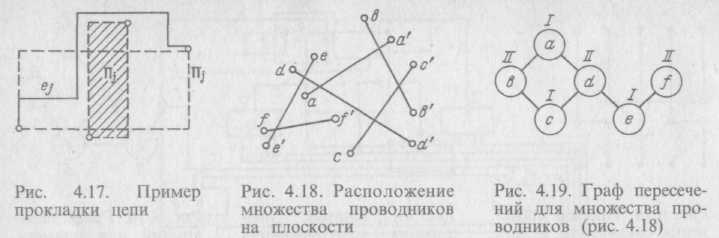
Рассмотрим теперь, каким образом организуется процесс расслоения, если он производится после трассировки, когда имеется совмещенный топологический эскиз. Теоретические осно­вы указанного метода разработаны Кодресом, Вейсманом и Бадером [59]. Постановку задачи расслоения рассмотрим на примере. Пусть задано расположение множества проводников М = (а, a'), (b, b') {с, с'), (d, d'), (e, e') (f, f') на плоскости (рис. 4.18). Сопоставим с ней граф перекрытии (пересечений) G_p = (E, U) (рис. 4.19), где e_i e E соответствует множеству проводни­ков, а ребра ueU—их пересечениям. Задача сводится к нахожде­нию двухцветной раскраски G_p, при которой суммарное число ребер, соединяющих одноцветные вершины, будет минимально. Это равносильно выделению в G_p максимального по числу ребер бихроматического подграфа. На основе известного свойства, состоящего в том, что граф является бихроматическим тогда, и только тогда, когда он не содержит циклов нечетной длины, используют процедуру раскраски, основанную на решении задачи линейного программирования. В нашем случае граф бихроматический и расслоение имеет вид: I — {(а, а'), (с, с'), (е, е')} и II — {(b, b') (d, d') (f, f')}.

Ввиду того, что в настоящее время отсутствуют критерии выделения максимальных n-хроматических подграфов в исходном, рассмотренные методы не применимы для n-слойных систем. Поэтому здесь используют эвристические процедуры раскраски в е цветов с последующим последовательным заполнением слоев оставшимися соединениями.

Рассмотрим алгоритм решения задачи для неограниченного числа слоев. Пусть для каждой цепи е_i задано в общем случае несколько вариантов реализации связывающего дерева {d_i^j/j=1,...,2} 2, ..., п) (в простейшем случае п=1). Особенность задачи состоит в том, чтобы для каждой пары выводов, для которых п> 1, выбрать одно соединение, приводящее к минимизации требуемого числа слоев.

Решение проводится в два этапа: на первом определяются максимальные внутренне устойчивые множества графа пересече­ний G_p, а на втором находится его минимальная или квазимини­мальная раскраска.

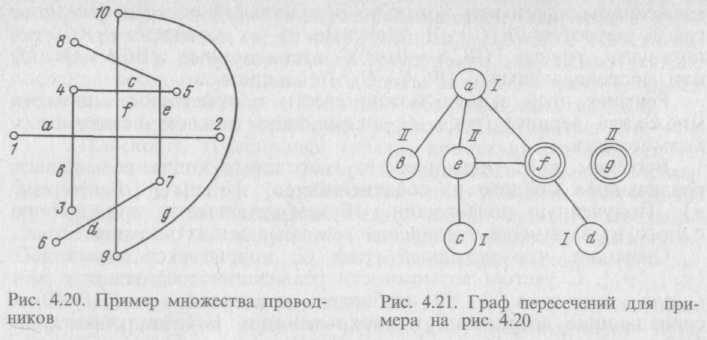
Рассмотрим пример (рис. 4.20). Применив алгоритм определения семейства независимых подмножеств (1.3), получим, что G_p (рис. 4.21) имеет следующие максимальные независимые подмножества (НП):

Имея семейство ф = {ф₁, ф₂, ф₃, ф₄}, можно переходить ко второму этапу, связанному с нахождением минимальной, квазиминимальной или локально

оптимальной раскраски вершин графа пересечений Gp . В зависимости от сложности КС ис­пользуют точные (ВСА = О (п!)), итерационные (ВСА = О(n²)) или последовательные (ВСА = О(n)) алгоритмы.

Решение этой задачи можно свести к отысканию покрытия множества вершин графа G_p наименьшим числом независимых подмножеств.

Выделим в Е подмножества, соответствующие возможным реализациям каждого из соединений: {a}, {b}, {с}, {d}, {e}, {f}, {g}. Полученную информацию будем учитывать при выборе одного из вариантов соединения в покрывающих подмножествах.

Очевидно, что исходный граф G_p покрывается двумя НП {ф₁} {ф₂}. С учетом возможности реализации соединения g или f для контактов 9—10 выбираем соединение g и, удаляя совпадающие соединения из покрывающих НП, получаем раз­биение на два слоя: I —{а, с, d}, II —{g, e, b}. Необходимо отметить, что если бы рассматривалось только одно соединение для контактов 9, 10, то для решения задачи потребовалось бы три слоя.

Рассмотрим эвристический алгоритм, позволяющий сократить межслойные переходы для ортогонального расслоения.

1. Выделить все непересекающиеся отрезки цепей и пометить их. (Очевидно, их можно назначить в любой из слоев без вынесения межслойных переходов.)

2°. Выделить в множестве непомеченных отрезков подмножест­во, любой из отрезков которого смежен не менее чем с одним отмеченным отрезком цепи.

3°. Поместить каждый из отрезков zeZ' в тот слой, в котором располагаются помеченные, смежные с ним отрезки. При наличии нескольких смежных отрезков выбрать тот, при размещении которого требуемое число межслойных переходов наименьшее.

4°. Пометить размещенный отрезок.

5°. Если z' = 0, переход к 6°, иначе — переход к 3°.

6 . Конец работы алгоритма.

Здесь ВСА равна О(п²)!. Следует отметить, что выбор того или иного алгоритма расслоения является нетривиальной задачей, требующей тщательного анализа исходных требований. Для расслоения во время трассировки в основном используют методы динамического программирования или последовательные алгорит­мы с оценкой каждого шага и возвратом назад в случае улучшения предыдущего результата.