4.1. Постановка задачи и классификация алгоритмов трассировки

Трассировка соединений является, как правило, заключительным этапом конструкторского проектирования РЭС и состоит в определении линий, соединяющих эквипотенциальные контакты элементов, и компонентов, составляющих проектируемое устройство.

Задача трассировки — одна из наиболее трудоемких в общей проблеме автоматизации проектирования РЭС. Это связано с несколькими факторами, в частности с многообразием способов конструктивно-технологической реализации соединений, для каж­дого из которых при алгоритмическом решении задачи приме­няются специфические критерии оптимизации и ограничения. С математической точки зрения трассировка — наисложнейшая задача выбора из огромного числа вариантов оптимального решения.

Одновременная оптимизация всех соединений при трассировке за счет перебора всех вариантов в настоящее время невозможна. Поэтому разрабатываются в основном локально оптимальные методы трассировки, когда трасса оптимальна лишь на данном шаге при наличии ранее проведенных соединений.

Основная задача трассировки формулируется следующим об­разом: по заданной схеме соединений проложить необходимые проводники на плоскости (плате, ТЭЗ, кристалле и т. п.), чтобы реализовать заданные электрические соединения с учетом заранее заданных ограничений. Основными являются ограничения на ширину проводников и минимальные расстояния между ними.

Исходной информацией для решения задачи трассировки соединений обычно являются список цепей, параметры конструк­ции элементов и коммутационного поля, а также данные по размещению элементов.

Критериями трассировки могут быть процент реализованных соединений, суммарная длина проводни­ков, число пересечений проводников, число монтажных слоев, число межслойных переходов, равномерность распределения про­водников, минимальная область трассировки и т. д. Часто эти критерии являются взаимоисключающими, поэтому оценка ка­чества трассировки ведется по доминирующему критерию при выполнении ограничений по другим критериям либо применяют аддитивную или мультипликативную форму оценочной

функции, например следующего вида: F = Σ λ_į f_i, где F—аддитивный критерий;

p

λ_į весовой коэффициент; f_i— частный критерий; р — число частных критериев.

Задача трассировки всегда имеет топологический и метри­ческий аспекты. Топологический аспект связан с выбором допусти­мого пространственного расположения отдельных фрагментов соединений без фиксации их конкретного месторасположения при ограничениях на число пересечений и слоев и т. п. Метрический аспект предполагает учет конструктивных размеров элементов,

соединений и коммутационного поля, а также метрических ограничений на трассировку.

В известных алгоритмических методах решения задачи трасси­ровки метрический аспект присутствует всегда, а топологи­ческий— в большей или меньшей степени. Все существующие методы трассировки можно подразделить на две большие группы: последовательные и параллельные.

В последовательных методах трассы проводят одну за другой последовательно, при этом проведение какой-либо трассы а на (i— 1)-м шаге может затруднить проведение трассы b на i-м шаге, так как является препятствием для проведения трассы b. Следовательно, особенно актуальным для последовательных ал­горитмов трассировки является предварительное ранжирование (упорядочение) соединений до трассировки.

Существуют различ­ные стратегии упорядочения, основанные, в частности, на длине соединений, степени охвата соединением других соединений и др. Однако объективных оценок эффективности таких методик в на­стоящее время нет, поэтому наиболее разумными представляются использование нескольких вариантов очередности и выбор из них наилучшего.

Задачу трассировки можно условно представить в виде четырех последовательно выполняемых этапов:

определение перечня соединений;

размещение по слоям;

определение порядка соединений;

трассировка проводников.

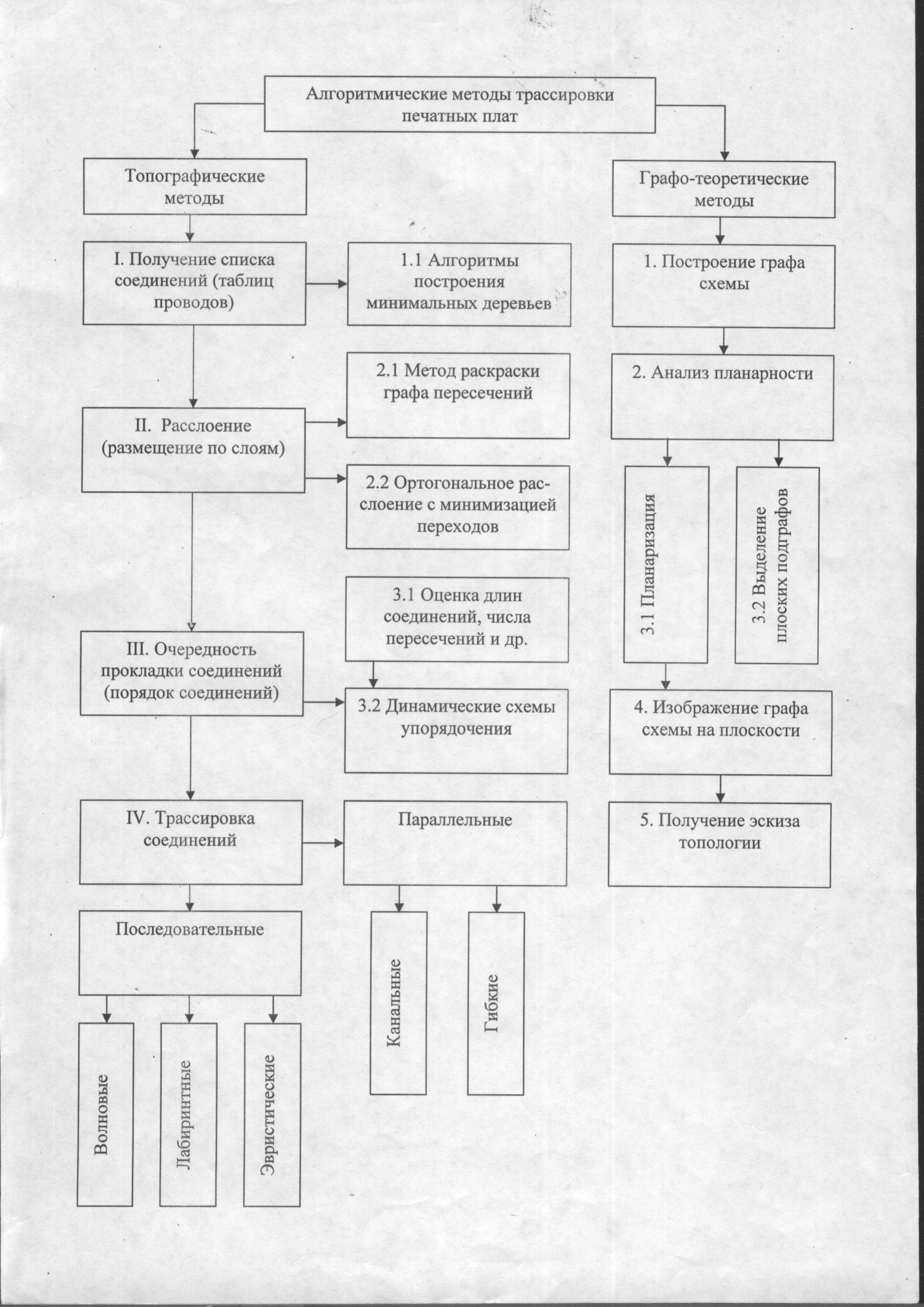
На первом этапе формируется точный список, указывающий, какие соединения (цепи или фрагменты цепей схемы) должны быть проведены.

На втором этапе предпринимается попытка точно решить, где каждое соединение может располагаться.

На третьем этапе определяется порядок соединений для каждого слоя,

т. е. указывается, когда каждый проводник, помещенный в этот слой, будет проведен.

На четвертом этапе дается ответ, каким образом должно быть проведено каждое соединение.

Рассмотрим указанные этапы подробнее.

Исходная информа­ция для первого этапа — это перечень соединений контактов каждого элемента с контактами других элементов. Одиночные контактные соединения записываются непосредственно в перечень соединений (матрицу цепей или список). Трудность при реализации возникает тогда, когда один контакт необходимо соединить с несколькими контактами. Для решения этого вопроса исполь­зуют алгоритмы построения кратчайших покрывающих деревьев Прима или Штейнера. На этом этапе ЭВМ не производит соединений, она только решает, какие проводники должны быть оттрассированы.

При определении перечня соединений необходимо также решать вопросы распределения контактов элементов по контактам разъема. Часто на практике пытаются исключить пересечение при проведении прямых линий между контактами элементов и соответствующими им контактами разъема. При трассировке многие элементы имеют логически эквивалентные контакты. Поэтому для упрощения трассировки просматривают проводники, подходящие к таким контактам, и при необходимости заменяют их друг на друга. Правило при замене проводников обычно заключается в исключении пересечений прямых линий.

На втором этапе решается задача размещения проводников по слоям. Она сводится к построению плоской укладки графа коммутационной схемы (КС). Окончательный вариант размещения по слоям можно улучшить, если проанализировать каждый проводник.

На третьем этапе производится исследование каждого слоя с целью точного определения момента, когда можно будет трассировать каждый проводник, другими словами — определить порядок обработки проводников в каждом слое. Для двух проводников существует правило выбора: если контакт В появ­ляется в прямоугольнике А, т. е. в прямоугольнике, имеющем в противоположных углах контакты проводника, то проводник В надо трассировать первым. К сожалению, не всегда это правило применимо. Сформулируем общее эвристическое правило Айкерса о порядке трассировки проводников. Проводники трас­сируются в порядке приоритетных номеров. Приоритетный номер проводника V равен числу контактов в прямоугольнике W. На практике обычно короткие горизонтальные и вертикальные от­резки проводников трассируются первыми, далее трассируются окружающие их почти вертикальные и горизонтальные провод­ники. В заключение трассируются длинные соединения, которые по отношению к другим чаще располагаются с внешней стороны.

Обычно проблему размещения соединений по слоям рассма­тривают как задачу раскраски специального графа. Далее про­изводится исследование каждого слоя с целью определения порядка обработки соединений внутри каждого слоя. После того как все соединения распределены по слоям и определен порядок их обработки, решается задача трассировки фрагментов всех цепей, что и выполняется на четвертом этапе.

Четвертый этап трассировки является основным, наиболее трудоемким, определяющим эффективность и качество всей задачи трассировки. На рис. 4.1 приведена классификация алгоритмов трассировки этого этапа.

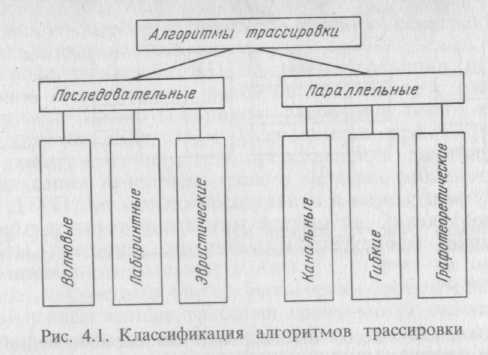
К волновым относятся алгоритмы, основанные на идеях динамического программирования на дискретном рабочем поле (ДРП). В настоящее время разработано огромное число моди­фикаций волнового алгоритма, предложенного Ли еще в 1961 г., однако все они сохраняют его основной недостаток: большие объемы вычислений и памяти ЭВМ. Временная сложность волнового алгоритма составляет O(MN), где N—число клеток ДРП; М — число точек, подлежащих соединению. Эффективное использование волновых алгоритмов возможно лишь для ДРП с числом клеток не более 10⁵, при этом время трассировки составляет несколько часов работы ЭВМ. Число неразведенных трасс обычно не превышает 10%.

Основная идея лабиринтных алгоритмов состоит в отыскании пути между двумя ячейками ДРП посредством последовательного обхода преград в лабиринте, образованном занятыми и свобод­ными ячейками. В отличие от волнового алгоритма поиск носит направленный характер, поэтому время поиска сокращается. Алгоритмы обычно обеспечивают разводку около 80% соединений.

Эвристические алгоритмы трассировки эффективны, как прави­ло, только на начальных стадиях трассировки, когда на плоскости мало преград. Основная идея состоит в генерации самых длинных незанятых отрезков в направлении цели с эвристическими прие­мами обхода препятствий.

В параллельных алгоритмах трассировки в начале определяется допустимое взаимное расположение трасс, которое оптимизи­руется по выбранному критерию, и лишь потом трассы фикси­руются на коммутационном поле.

Канальные алгоритмы основаны на возможности в некоторых случаях регулярного разбиения коммутируемого поля (КП) на каналы и трассировки внутри каналов вертикальными и горизонтальными отрезками. Алгоритмы работают быстро, однако для них акту­альна проблема качества получаемых решений. Отметим, что канальным алгоритмом свойствен иерархический подход к трасси­ровке, когда исходная задача декомпозируется на несколько подзадач. При этом на каждом иерархическом уровне в зави­симости от его специфики целесообразно применение различных методов трассировки.

В алгоритмах гибкой трассировки на первом этапе строятся модели топологии для трасс цепей на дискретном топологическом рабочем поле (ДТРП) (без жесткой фиксации), а на втором этапе — модели геометрии, которые метрически точно определяют конфигурацию и месторасположение каждой трассы на КП.

В графотеоретических методах используют графовые модели элементов и компонентов схем, на основе которых синтезируется топологический эскиз проектируемого устройства. На следующем этапе решается задача метризации топологического эскиза.

Рассмотрим модели КП для указанных алгоритмов трасси­ровки. Для волновых и лабиринтных методов используется ДРП следующего вида.

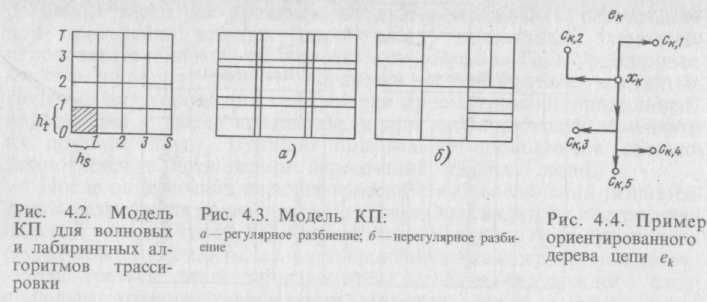
Пусть задана прямоугольная система координат SOT (рис. 4.2) на КП и выбраны единицы измерения h_s и h_t соответственно вдоль осей OS к ОТ. Проведем через точки осей с координатами ah_s и ah_t, где а=1, 2, ..., прямые, параллельные осям координат. Тогда плоскость КП может быть разбита на элементарные прямоугольные ячейки размером h_sxh_t, а прямые разбиения образуют координатную сетку с шагом h_s по оси OS и шагом h_t по оси ОТ. Совокупность элементарных ячеек, на которые разбивается КП, называется ДРП. Значения h_s и h_t выбираются в зависимости от площади КП, допустимой плотности рас­положения выводов элементов и проводников.

Модель КП для канальных и эвристических алгоритмов, так же как и в предыдущем случае, разбивается на прямоугольные области, называемые каналами, но в отличие от предыдущей модели разбиение определяется расположением выводов элемен­тов. Если элементы однотипны и размещены на плоскости регулярно, то разбиение на каналы также будет регулярным, в противном случае — нерегулярным (рис. 4.3, a, б).

Длина стороны любого канала, параллельной преимуществен­ному направлению трасс на слое, называется длиной этого канала, а длина другой стороны — его шириной. Число трасс, которые могут пересечь боковую границу канала, называется пропускной способностью канала.

Регулярное разбиение КП на прямоугольники не вызывает затруднений. Нерегулярное разбиение несколько сложнее. Жела­тельно, чтобы прямоугольников разбиения было как можно меньше, так как при этом уменьшается время трассировки, а также размеры таблиц для представления данных.

Для описания топологии трасс в методах гибкой трассировки строится ДТРП. Ее можно представить в виде графа G_r = (X_r, U_r), где Х_r соответствует контактам элементов, характерным точкам края платы, внешним контактам, запрещенным зонам; U_r — ли­ниям, соединяющим элементы х  Х_r.

Вообще, дискретами могут быть грани любой конфигурации. При этом ненасыщенные трассами грани могут сжиматься, а те, через которые проходит большое число трасс,— растягиваться.

Приведем математическую формулировку задачи трассировки электрических соединений. Исходными данными являются коммутационная схема (КС), конструкция плоскости, результаты размещения элементов. Будем считать, что все трассы прокладываются в одном слое; КС определяют подмножества непересекающихся множеств контактов координаты которых заданы. Контакты каждого подмножества С_рi = С_р в КС объединены электрическим соединени­ем, т. е. цепью (см. 1.5). Необходимо соединить контакты цепей таким образом, чтобы фрагменты различных цепей не пересекались и располагались друг от друга на расстоянии не меньше заданного. Математической моделью конструкции является регулярная коор­динатная сетка (граф G_r), соответствующая ДРП. Отметим, что размеры ячеек ДРП обычно определяют площадью, заданной для трассировки плоскости, ограничениями на плотность расположения контактов и соединений. Пусть ячейки ДРП имеют форму квадратов и через каждую ячейку может проходить только одно соединение, где Х₃ — множество запрещенных для проведения трасс ячеек ДРП. Каждой ячейке ДРП будет соответ­ствовать вершина Тогда любую цепь l_t КС можно представить в виде ориентированного дерева (граф КС) с корнем в произвольно выбранной вершине х_к (рис. 4.4).

Тогда дерево Тk. можно рассматривать как объединение простых путей (х_к, i Причем каждый путь (х_к, с_кr) состоит из дуг Uij = (Xi, Xj), которые соответствуют прохождению трассы из ячейки х_i, в соседнюю ячейку Хj

Вводят булевы переменные

Длина цепи будет выражаться числом покрываемых ячеек, т. е. вершин G_r, и определяться как L_k = ΣΣ y^k_{i j} + 1,

где — множество ячеек, соседних с i и принадлежащих X_t \ Х₃;

п_к = |Т|-1 — число вершин дерева.

На основе вышеизложенного критерий трассировки записыва­ют так:

Для каждого пути (х_к, с_кr) обычно задаются следующие ограничения:

из вершины х_к выходит только одно ребро, принадлежащее пути;

в каждую вершину х_к не должны заходить никакие ребра;

в вершины с_кr заходит единственное ребро из пути (х_к, с_к,r);

в вершинах с_к,r нет выходящих ребер;

в любой вершине не должно быть обрыва пути

(х_k с_к,r).

Для учета требования непересечения различных трасс вводят ограничения

Минимизация критерия L с учетом рассмотренных ограни­чений может представлять собой ЗЦП, решение которой (см. гл. 1) будет определять трассировку соединений. Заметим, что из-за громоздкости и длительности решения в практических задачах в основном используют эвристические алгоритмы трас­сировки с минимизацией описанного критерия или его моди­фикаций.

4.2. ТРАССИРОВКА ПРОВОДНЫХ СОЕДИНЕНИЙ

В зависимости от конструктивной реализации связей выделяют трассировку проводных соединений, трассировку печатных соеди­нений, трассировку межсоединений на кристалле БИС. Здесь рассмотрим вопросы трассировки проводных соединений, а также одностороннего, двустороннего и многослойного монтажа на печатных платах.

Среди всех конструктивно-технологических реализаций связей проводной монтаж с точки зрения практического решения задачи трассировки наиболее прост. Объясняется это тем, что проводники изолированы друг от друга и не стоит задачи об ограничениях на пересечения. Поэтому основным критерием трассировки про­водных соединений является суммарная длина соединений.

Для проводного монтажа задача трассировки сводится к по­строению на вершинах графа дерева с минимальной суммарной длиной ребер, при этом вершины графа моделируют соединяемые контакты, а ребра — межсоединения. Единственное ограничение накладывается на максимальную локальную степень вершины, так как технологически целесообразно подсоединять к одному контакту не более определенного конечного числа соединений. Задача построения минимального дерева формулируется сле­дующим образом. Пусть Р = {p_1, р₂, ..., р_п}- множество точек плоскости, соответствующих выводам произвольной цепи. Рассмо­трим полный граф К_п=(Х, U), вершины которого х_iеХ соответ­ствуют выводам цепи, а ребра u_jе U с приписанным к ним весом характеризуют соединения между парами выводов. Значение может представлять линейную комбинацию нескольких характери­стик соединения где ц,-— весовые коэффициенты; d_s — некоторая характеристика соединения и_j

Теперь исходная задача сводится к определению в графе G дерева, включающего все вершины хеХ и имеющего минималь­ный суммарный вес ребер, т. е. КПД (см. 1.2). Решение задачи дано в работах Краскала, Добермана, Уйэнбергера и Прима [3, 4, 6, 12, 22, 38, 44, 59, 65, 70].

Под расстоянием между вершинами графа будем понимать значение мю(Uj), приписанное соответственно ребрам графа. Рас­стоянием от вершины до изолированного фрагмента будем считать минимум расстояний от отдельных вершин до фрагмента. Алгоритм Прима построения кратчайшего покрывающего дерева или цепи с п выводами может быть описан теперь следующим образом.

1°. Для произвольного вывода цепи найти ближайший и про­вести соединение.

2°. На каждом последующем шаге 1=2, 3, ..., п из множества неподсоединенных выводов выбрать тот, который находится ближе остальных (в указанном выше смысле) к группе уже связанных выводов, и подсоединить его к этой группе по кратчайшему пути.

Рассмотрим пример. Пусть необходимо соединить цепью эквипотенциальные контакты, обозначенные цифрой 1 на рис. 4.5, а. Для этого примера по шагам рассмотрено решение задачи построения КПД с помощью алгоритма Прима на рис. 4.5,б—д.

Построенное по алгоритму Прима КПД обладает тем свойством, что степень любой вершины не превышает 6. Как правило, при разработке монтажных

схем проводных соединений вводится ограничение на максимальное число соединений, подходящих к одному выводу. Если \<6, то необходимо использовать специальные алгоритмы построения КПД. Для решения такой задачи часто используются алгоритмы, основанные на методе ветвей и границ, однако при анализе большого числа цепей предпочтение отдают эвристическим алгоритмам.

Например, рассмотрим модифицированный алгоритм Прима. Всякая изолиро­ванная вершина соединяется с ближайшей, не соединенной с X другими вершинами; всякий изолированный фрагмент соединяется кратчайшим ребром с ближайшей вершиной, не соединенной с X другими вершинами.

В некоторых случаях помимо ограничения на степени вершин задаются начальная и конечная точки цепи. Это имеет место, например, при разработке монтажных схем для высокочастотных цепей, когда необходимо в определенной последовательности связать источник сигнала и несколько нагрузок. Иногда задача сводится к построению кратчайшего пути между двумя заданными выводами, проходящего через все остальные выводы цепи. Данная задача родственна задаче о маршруте коммивояжера, а следуя терминологии теории графов,— это задача построения кратчайшей гамильтоновой цепи между задан­ными начальной и конечной вершинами.

Рассмотрим алгоритм, дающий приближенное решение этой задачи. Основой алгоритма являются (п — 1)-й шаговый процесс выбора кратчайших ребер в полном графе Кn проверки каждого ребра на выполнение ограничений задачи и со­ставление из выбранных ребер пути, соединяющего заданные точки.

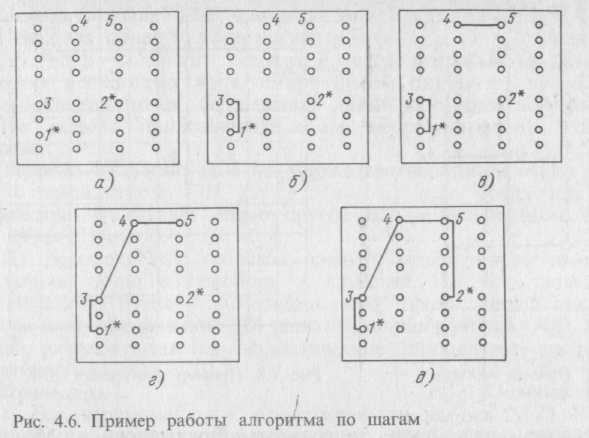
Приведем пример. Пусть задано расположение точек, подлежащих соединению на плате (рис. 4.6,а). Составим упорядоченную по возрастанию длин последова­тельность ребер полного графа К_n: (1*—3), (1* — 2), (2* — 3), (4—5), (3-4), (3 — 5), (1*—4), (2* —5), (2* —4), (1* — 5). Отметим, что 1* и 2* —соответственно начальная и конечная точки пути.

Очередное ребро i = 1, 2, ..., п-1 выбирается по порядку из этой последовательности при выполнении следующих условий:

1. Ребро не соединяет заданные конечную и начальную точки (1* и 2*).

2. При включении ребра в путь степень вершин, соединяемых этим ребром, не превышает заданной (лямбда = 1 для начальной и конечной точек и Х=2 для остальных точек).

3. Ребро не образует цикла с ребрами, уже включенными в путь.

4. При включении в путь любого ребра (кроме (n-l)-ro) начальная и конечная точки остаются несвязанными.

Условия 1 — 3 непосредственно вытекают из ограничений задачи. Условие 4 препятствует образованию тупиковых ситуаций, когда дальнейшее формирование пути становится невозмож­ным— все подсоединенные точки, кроме начальной и конечной, имеют степень лямбда = 2. Пошаговый процесс формирования пути изображен на рис. 4.6, а — д. Среднее изменение длин монтажных соединений для данного алгоритма по сравнению с оптимальным решением составляет порядка 5%.

Задача построения КПД усложняется, если при соединении множества вершин (контактов цепи) разрешается использование дополнительных точек соединения. В общем виде данная задача формируется так: для заданных x_t, x₂,..., х_п точек плоскости построить КПД с п'>=п вершинами — и называется задачей Штейнера (ЗШ). Обычно решение ЗШ рассматривают в областях прямоугольной конфигурации. Известно, что для п <= 5 известно решение ЗШ, в общем же случае известны условия, которым должны удовлетворять деревья Штейнера (ДШ) и эвристические алгоритмы. Дополнительные точки, вводимые при построении КПД, называют точками Штейнера (ТШ).

Приведем ряд лемм, полученных Фридманом и Меноном, дающих необходимые условия существования и построения ДШ [65 ].

Лемма 4.1. Для п вершин, которые должны быть соединены между собой, всегда можно построить ДШ, в котором каждая ТШ g_t соединена по крайней мере с тремя другими.

Лемма 4.2. Для множества вершин {х₁, х₂, х₃}, которые дол­жны быть соединены, координаты ТШ g, минимизирующей

будут S_cp, Т_ср и справедливо выражение

где S_cp, Т_ср — средние значения S_t (i = 1, 2, 3) и t_i (j=1, 2, 3); P(х₁, х₂, х₃)— длина периметра прямоугольника, построенного на вершинах x_l x₂, х₃; d(g, п_i) — прямоугольное расстояние между g и ni.

На рис. 4.7 показан пример, иллюстрирующий условия леммы 4.2 при построении ДШ, соединяющего вершины x_t, x₂, х₃. Точка Штейнера g имеет координаты S_g=3, t_g = 5.

Лемма 4.3. Дано ДШ, состоящее из хi,- точек плоскости. Пусть ТШ g соединена только с тремя вершинами x_t, x₂, х₃. Тогда g находится внутри прямоугольника, построенного на точках x_i, x₂, х₃, и ТШ единственна.

Следствие 4.1. Для заданного множества вершин x_t, x₂, х₃ ДШ содержит одну ТШ g с координатами (S_cp, T_cp), если она не совпадает ни с одной из вершин х₂ x₂, х₃ и суммарная длина ребер ДШ равна

Лемма 4.4. Дано ДШ на множестве X={x_t, x₂, ..., х„}, а ТШ этого дерева образуют множество g = {g_lt g₂, ..., g_k} Если g_xс g и g_E принадлежит I то g_x содержит элемент g_1k, соединенный не менее чем с двумя вершинами из I, в противном случае g₁ пусто. Здесь I—множество точек пересечения линий координатной сетки.

На основе приведенных лемм сформулирована известная теорема. ■

Теорема 4.1. Дано ДШ на множестве вершин Х = {х_1, х₂, ..., х„} с множеством ТШ g = {g₁ g₂, ..., g_k} Тогда для этого множества существует такое другое ДШ с множеством ТШ g', что

Из рассмотрения теоремы следует метод определения ДШ на основе полного перебора в качестве ТШ всех возможных подмножеств точек /. Очевидно, что такой метод применим только при построении ДШ для небольшого числа ТШ. В этой связи разрабатываются эвристические процедуры построения квазиминимальных ДШ.

Процедура 1.

1. Все вершины х_i принадлежат Х проектируются на ось S(T).

2°. Расстояние от наименьшей до наибольшей координаты делится пополам, и из этой точки i принадлежит I или [i] при iне принадлежащем I проводится перпендикуляр (столб Штейнера).

3°. Из каждой вершины x_ieX опускается перпендикуляр до пересечения со столбом Штейнера.

4°. Построено ДШ. Конец работы алгоритма.

Данный алгоритм очень прост, ВСА равна О(п), но в смысле минимума суммарной длины проводников результаты далеки от совершенства.

Процедура 2 (Алгоритм Ханана).

1. Все множество вершин хiеX разбивается на классы S_o, S₁,... ..., S_i в порядке возрастания координаты Si, так, чтобы у всех вершин одного класса была одинаковая координата S_i.

2^е. Анализируется множество вершин класса S₀, и соединяются перпендикуляром все вершины этого множества с точкой S_min оси S.^тш

3°. Образуется множество I', состоящее из всех точек I, которые были до этого соединены с произвольной вершиной x_i, включая и вершины хi, строящегося ДШ.

4°. Выбирается следующее множество S_i+1, имеющее наимень­шую координату S. Определяются точка i_mel' и вершина хj еS_{i + 1}, для которых

Другими словами, хi, находится на кратчайшем расстоянии от рассматриваемого фрагмента ДШ в классе S_{i + 1}. Точка i_m

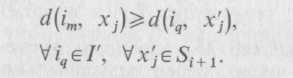
с координатами (s_m, tm) соединяется с вершиной Xj с координатами (s_j, tj) двузвенной ломаной линией. Причем звенья параллельны координатным осям S и Т.

5 . Для каждой вершины производятся операции, аналогичные 4 . При этом вершина соединяется с ближайшей в 1'.

6°. Пункты 4 и 5 повторяются для всех по порядку множеств Sj до построения ДШ.

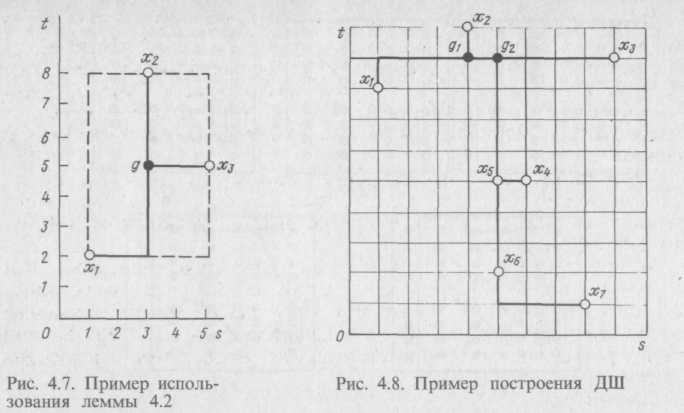
Отметим, что существует большое число модификаций описан­ных процедур. Можно проводить упорядочивание координат не по увеличению S(T), а по уменьшению S(Т). Временная сложность алгоритма процедуры 2 составляет О (сn²). На рис. 4.8 показана реализация процедуры 2 с упорядочиванием вершин в 1 в порядке убывания координат S. Суммарная длина ДШ составляет 22 условные единицы, при этом число ТШ равно 2.

Для построения ДШ можно использовать методы ПВГ, ПВШ или ветвей и границ в зависимости от требований на ВСА.