Методы растрирования кривых второго порядка

1. Вывод окружности

В растр нужно разлагать не только линейные, но и другие, более сложные функции. Разложению конических сечений, т. е. окружностей, эллипсов, парабол, гипербол, было посвящено значительное число работ. Наибольшее внимание, разумеется, уделено окружности.

1.1. Метод прямого вычисления координат

Рассмотрим окружность с центром в начале координат, для которой x²+y²=R² .

Согласно определению тригонометрических функций произвольная окружность радиуса R с центром в точке (x₀, y₀) может быть определена как множество точек A(x, y), координаты которых удовлетворяют системе уравнений:

	x = x0 + R cos        y = y0 + R sin ,	где   [0;2).



Построим процедуру, которая будет по одной координате ставить восемь точек, симметричных центру окружности:

Void Circle_Pixel(int x0, int y0, int X, int y, int color); {

putpixel(x0 + x, y0 + y, color); putpixel(x0 + y, y0 + x, color); putpixel(x0 + y, y0 - x, color); putpixel(x0 + x, y0 - y, color); putpixel(x0 - x, y0 - y, color); putpixel(x0 - y, y0 - x, color); putpixel(x0 - y, y0 + x, color); putpixel(x0 - x, y0 + y, color);

}

Таким образом, можно написать программу рисование окружности по точкам:

Void Circle (int x0, int y0, int r, int color) {

for ( int x=0; x<=R/sqrt(2); x++) {

int y = (int)(sqrt(sqr(R)-sqr(x))); Circle_Pixel (x0, y0, x, y, color);

}

}

procedure my_circle(x,y,r:integer);

var alfa: integer;

begin

moveto(x+r,y);

for alfa:=1 to 360 do

{ угол измерятся в градусах }

lineto(round(x+r*cos(alfa*pi/360)), round(y+r*sin(alfa*pi/360)))

{ здесь используется радианная мера углов }

end;

Существенные временные затраты при реализации вышеотмеченной процедуры по сравнению процедурой circle становятся заметны при визуализации тысячи произвольных окружностей. Кроме того, на самом деле мы строим не окружность, а правильный 360-угольник. Развитие аппаратных средств и увеличение разрешающей способности дисплеев может привести к тому, что отличие многоугольника от окружности станет заметным на глаз. Это обусловливает бесперспективность приведенного алгоритма.

1.2. Алгоритм Брезенхема для вывода окружности

Реализация инкрементных алгоритмов изображения окружности несколько сложнее, чем при построении отрезка. Мы рассмотрим алгоритм построения растровой развертки окружности радиуса R с центром в начале координат. При этом задача сводится к генерации дуги окружности АВ, равной одной восьмой части окружности от 0 до 45° в направлении по часовой стрелке с исходной точкой построения A (R, 0). В этом случае координата окружности x является монотонно убывающей функцией координаты y. Остальные части окружности получают путем последующих отображений симметрии:

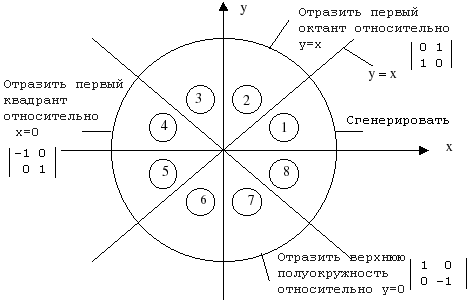
Рис. 1. Матрицы преобразований симметрии

Если сгенерирован первый октант, то второй октант можно получить зеркальным отражением относительно прямой у = х, что дает в совокупности первый квадрант. Первый квадрант отражается относительно прямой х = 0 для получения соответствующей части окружности во втором квадранте. Верхняя полуокружность отражается относительно прямой у = 0 для завершения построения. На рис. 1 приведены двумерные матрицы соответствующих преобразований.

П

m_H = |(x_i + 1)² + (y_i)² -R²|

m_D = |(x_i + 1)² + (y_i -1)² -R²|

m_V = |(x_i )² + (y_i -1)² -R²|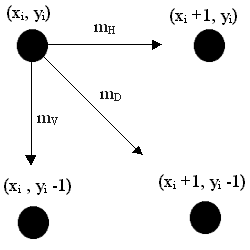

редполагается, что центр окружности и начальная точка находятся точно в точках растра. Для любой заданной точки (x_i, y_i) на окружности при генерации по часовой стрелке существует только три возможности выбрать следующий пиксел, наилучшим образом приближающий окружность: горизонтально вправо, по диагонали вниз и вправо, вертикально вниз. На рис. 3 эти направления обозначены соответственно m_H, m_D, m_V. Алгоритм выбирает пиксел, для которого минимален квадрат расстояния между одним из этих пикселов и окружностью, т. е. минимум из m_H, m_D, m_V.

Приступим к разбору ключевой идеи алгоритма. Пусть мы находимся в некоторой промежуточной фазе построения. Мы только что поставили точку (x_i, y_i) и теперь должны сделать выбор между точками 1(x_i+1, y_i-1) и 2(x_i+1, y):

Рис. 2

Реальная окружность может быть расположена относительно точек 1 и 2 одним из пяти способов 1-5. Если мы выбираем точку 1, то тем самым полагаем, что

(x_i+1)²+(y_i-1)²  R².

Если же выбираем точку 2, то допускаем, что

(x_i+1)²+(y_i)²  R².

Рассмотрим две погрешности ⁱ₁ и ⁱ₂:

ⁱ₁ = (x_i+1)²+(y_i-1)²-R²

ⁱ₂ = (x₁+1)²+(y_i)²-R²

и контрольную величину ⁱ = ⁱ₁+ⁱ₂.

При выборе точки на следующем шаге, станем руководствоваться следующим критерием:

если ⁱ > 0, выберем точку 1;

если ⁱ  0, выберем точку 2.

Обоснуем разумность такого выбора. Рассмотрим знаки погрешностей ⁱ₁ и ⁱ₂ и их влияние на знак контрольной величины ⁱ для всех пяти возможных положений окружности.

Для положения 1.

ⁱ₁ < 0, ⁱ₂ < 0  ⁱ₁+ⁱ₂ < 0  выбирается 2.

Для положения 2.

ⁱ₁ < 0, ⁱ₂ = 0  ⁱ₁+ⁱ₂ < 0  выбирается 2.

Для положения 3 возможны варианты (учитывая, что ⁱ₁ < 0, ⁱ₂ > 0).

Вариант 3.1. |ⁱ₁|  |ⁱ₂|  ⁱ₁+ⁱ₂ < 0  выбирается 2.

Вариант 3.2. |ⁱ₁| < |ⁱ₂| ⁱ₁+ⁱ₂ > 0  выбирается 1.

Для положения 4.

ⁱ₁ = 0, ⁱ₂ > 0  ⁱ₁+ⁱ₂ > 0  выбирается 1.

Для положения 5.

ⁱ₁ > 0, ⁱ₂ > 0  ⁱ₁+ⁱ₂ > 0  выбирается 1.

Далее получим выражение для контрольной величины ⁱ

ⁱ = ⁱ₁+ⁱ₂ = (x_i+1)²+(y_i-1)²-R²+(x_i+1)²+(y_i)²-R² = 2x_i²+2y_i²+4x_i-2y_i+3-2R².

Выражение для ⁱ⁺¹ существенным образом зависит от выбора следующей точки. Необходимо рассмотреть два случая: y_i+1 = y_i и y_i+1 = y_i-1.

ⁱ⁺¹ [при y_i+1 = y_i] = 2x²_i+1+2y²_i+1+4x_i+1-2y_i+1+3-2R² = 2(x_i+1)²+2y_i²+4(x_i+1)-2y_i+3-2R² = ⁱ+4x_i+6.

ⁱ⁺¹ [при y_i+1 = y_i-1] = 2x²_i+1+2y²_i+1+4x_i+1-2y_i+1+3-2R² = 2(x_i+1)²+2(y_i-1)²+4(x_i+1)-2(y_i-1)+3-2R² = ⁱ+4(x_i-y_i)+10.

Теперь, когда получено рекуррентное выражение для ⁱ⁺¹ через ⁱ, остается получить ¹ (контрольную величину в начальной точке.) Она не может быть получена рекуррентно, ибо не определено предшествующее значение, зато легко может быть найдена непосредственно

x₁ = 0, y₁ = R  ¹₁ = (0+1)²+(R-1)²-R² = 2-2R,

¹₂ = (0+1)²+R²-R² = 1

¹ = ¹₁+¹₂ = 3-2R.

Таким образом, алгоритм Брезенхема для построения окружности основан на последовательном выборе точек; в зависимости от знака контрольной величины ⁱ выбирается следующая точка и нужным образом изменяется сама контрольная величина. Согласно процедуре sim, процесс начинается в точке (0, R), а первая точка, которую ставит процедура, имеет координаты (xc, yc+r). При x = y процесс заканчивается.