Иерархия моделей

Накопленный человеческий опыт практического познания мира свидетельствует, что для конструктивного изучения системы необ­ходимо составить ее модель. Эта модель должна быть ориентирова­на на отражение именно тех свойств, которые представляют наи­больший интерес для исследователя или заказчика работ.

В экономических системах наибольший интерес, как правило, составляют процессы выработки и реализации управленческих ре­шений. Для обоснования решений необходимо обрисовать про­блемную ситуацию; определить область принятия решения; выявить факторы, влияющие на решение; подобрать приемы, методы и ап­парат формализации таким образом, чтобы решение было возмож­ным, а его результат - приемлемым.

В идеальном случае для принятия решения необходимо полу­чить выражение, связывающее цель системы со средствами ее дос­тижения. Такое выражение называют критерием функционирова­ния, показателем эффективности, целевой функцией, функцией цели или критериальной функцией. Однако, как бы его ни называ­ли, это выражение представляет собой закон, позволяющий оцени­вать эффективность того или иного пути движения к цели. С одной стороны, критерий отражает меру приближения к цели, а с другой - цену этого приближения.

Если такой закон известен, то он выражается в математической модели, с помощью которой осуществляется поиск рациональных решений. В такой ситуации задача исследования системы разреши­ма практически всегда. В дальнейшем речь может идти только о вычислительных сложностях. Если закон неизвестен, то стараются определить закономерности на основе статистических исследований и установить корреляционную зависимость между критерием и клю­чевыми факторами функционирования системы. Установление кор­реляционных зависимостей осуществляется в рамках эконометрических моделей. Если и этого не удается сделать, то выбирают или разрабатывают теорию, которая содержит утверждения и правила, позволяющие сформулировать концепцию, построить концептуаль­ную модель и на этой основе сконструировать механизм принятия решений. Если и теории не существует, то выдвигается гипотеза и на ее основе создается имитационная модель, с помощью которой исследуются возможные варианты решения.

В общем виде для ситуаций разной сложности процесс форми­рования критериальной функции для отображения проблемной си­туации можно представить, воспользовавшись многоуровневым описанием «слоев». Схема на рисунке представляет воз­можность составить определенное мнение о сложности, масштабно­сти и значимости исследовательских работ при построении модели проблемной ситуации в целях ее разрешения.

Если говорить о диссертационных исследованиях, то первые два уровня (близкие к проблемной ситуации) составляют поле для кан­дидатских работ, в то время как последующие два могут составить предмет докторской диссертации.

Классификация методов моделирования

Постановка любой задачи заключается в том, чтобы перевести ее вербальное (словесное) описание в формализованную форму. В случае относительно простых задач такой перевод осуществляется в сознании человека, который не всегда может объяснить, как он это сделал. Если полученная математическая модель опирается на фун­даментальный закон или подтверждается экспериментом, то этим доказывается ее адекватность отображаемой ситуации, и модель рекомендуются для решения задач того или иного класса.

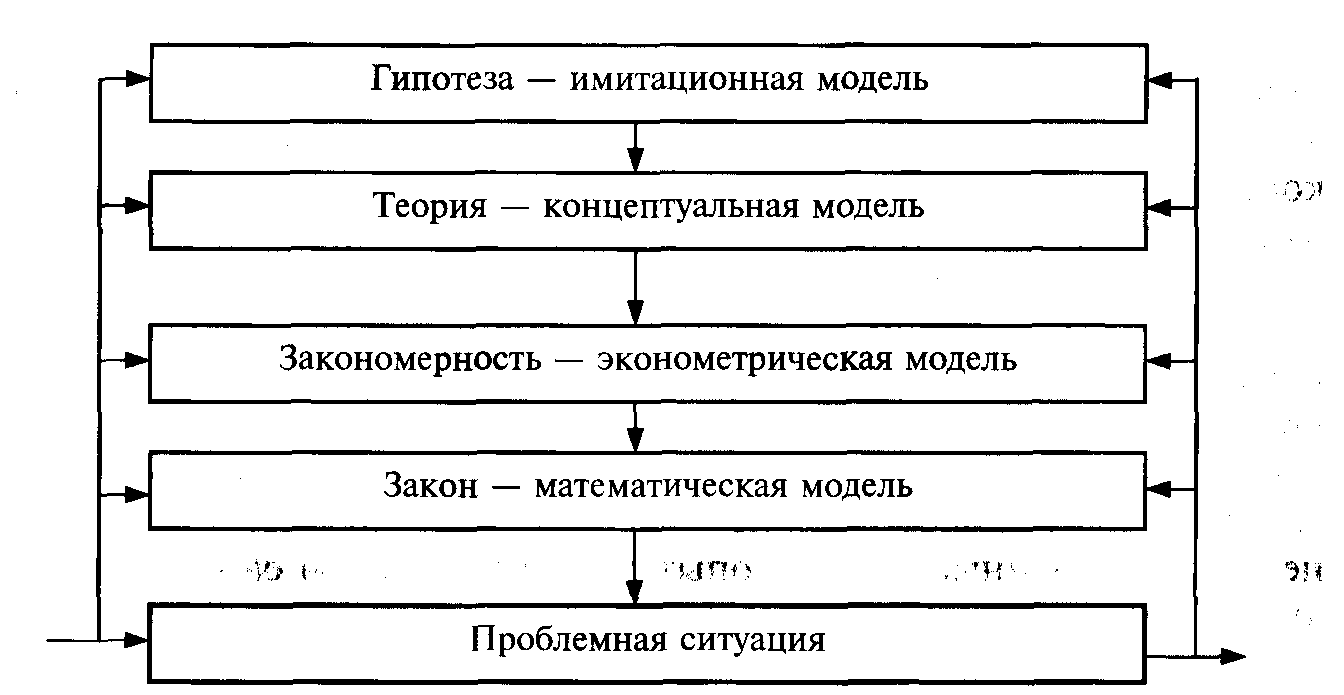
Рис. 2.1.2. Схема формирования критериальной функции для отображения

проблемной ситуации

По мере усложнения задач получение модели и доказательство ее адекватности усложняются. Более того, большинство реальных си­туаций в экономических и других социокультурных системах описы­вается моделями, которые должны постоянно корректироваться и развиваться. При этом возможно изменение не только модели, но и метода моделирования, что является свидетельством развития пред­ставления системного аналитика о моделируемой ситуации.

Для перевода вербального описания в формализованное в пер­вую очередь привлекается весь существующий математический ар­сенал. Именно необходимость постановки и решения трудно фор­мализуемых задач на протяжении многих лет являлась двигателем развития математических методов. Как ответ на необходимость до­казательства адекватности модели (на основе представительной вы­борки) и правомерности распространения ее экспериментальных результатов на всю генеральную совокупность, наряду с детермини­рованными аналитическими методами классической математики появилась теория вероятностей и математическая статистика.

Необходимость решения сложных практических задач в услови­ях большой неопределенности стимулировало развитие таких мате­матических направлений, как теория множеств, математическая логика, математическая лингвистка и теория графов. Необходи­мость количественной оценки качественных процессов в сложных динамических системах привела к развитию нового направления математического моделирования, заключающегося в использовании так называемых мягких моделей.

С другой стороны, для коллективного решения масштабных ор­ганизационных задач (реструктурирования предприятия, слияния двух и более хозяйствующих субъектов, проведения выборов и т.д.)» когда один человек не может принять решение о выборе факторов, влияющих на достижение цели, не в состоянии определить сущест­венные взаимосвязи между целями и средствами, не обладает всем необходимым спектром знаний для успешного решения проблемы, в различных областях деятельности стали развивать специальные приемы и методы - мозгового штурма, Дельфи, интерактивного моделирования и т.д. В конечном итоге эти методы позволяют формализовать существующие в исследуемой предметной области неформализованные знания, опыт и традиции и тем самым обеспечить перевод вербальной модели в формализованный вид.

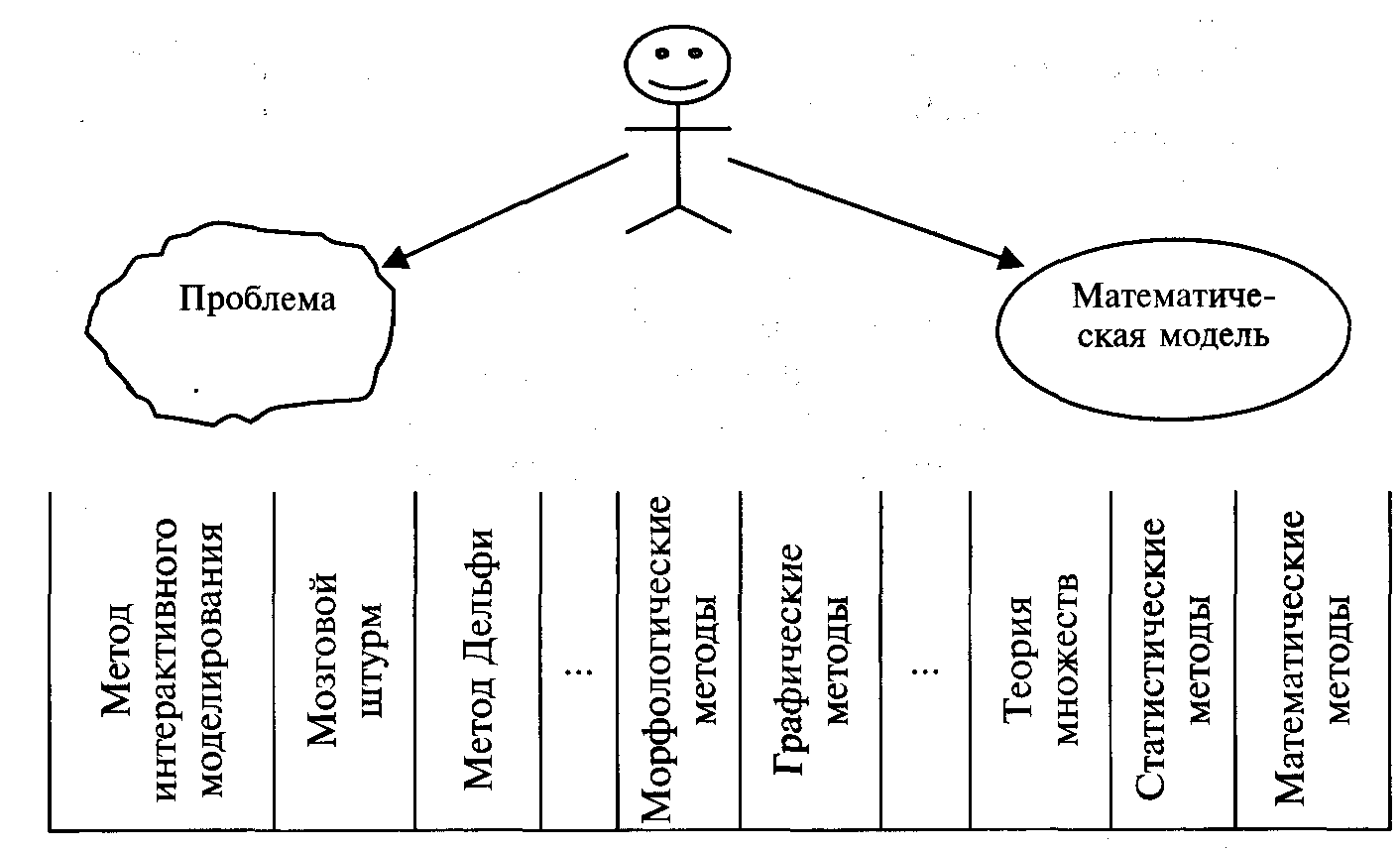
Рис. 2.1.3. Шкала методов формирования проблемы

Таким образом, между проблемой, описанной на содержатель­ном уровне, и математическими моделями сложился спектр мето­дов, которые помогают формализовывать вербальные описания проблемных ситуаций, интерпретировать формализованные описа­ния и увязывать их с действительностью

Развитие методов моделирования идет не так последовательно, как это показано на рисунке. Методы возникают и развиваются од­новременно. Более того, при решении сложных задач человек, как

правило, попеременно выбирает методы из левой и правой части спектра, совсем не соблюдая их эволюционность и наследственность.

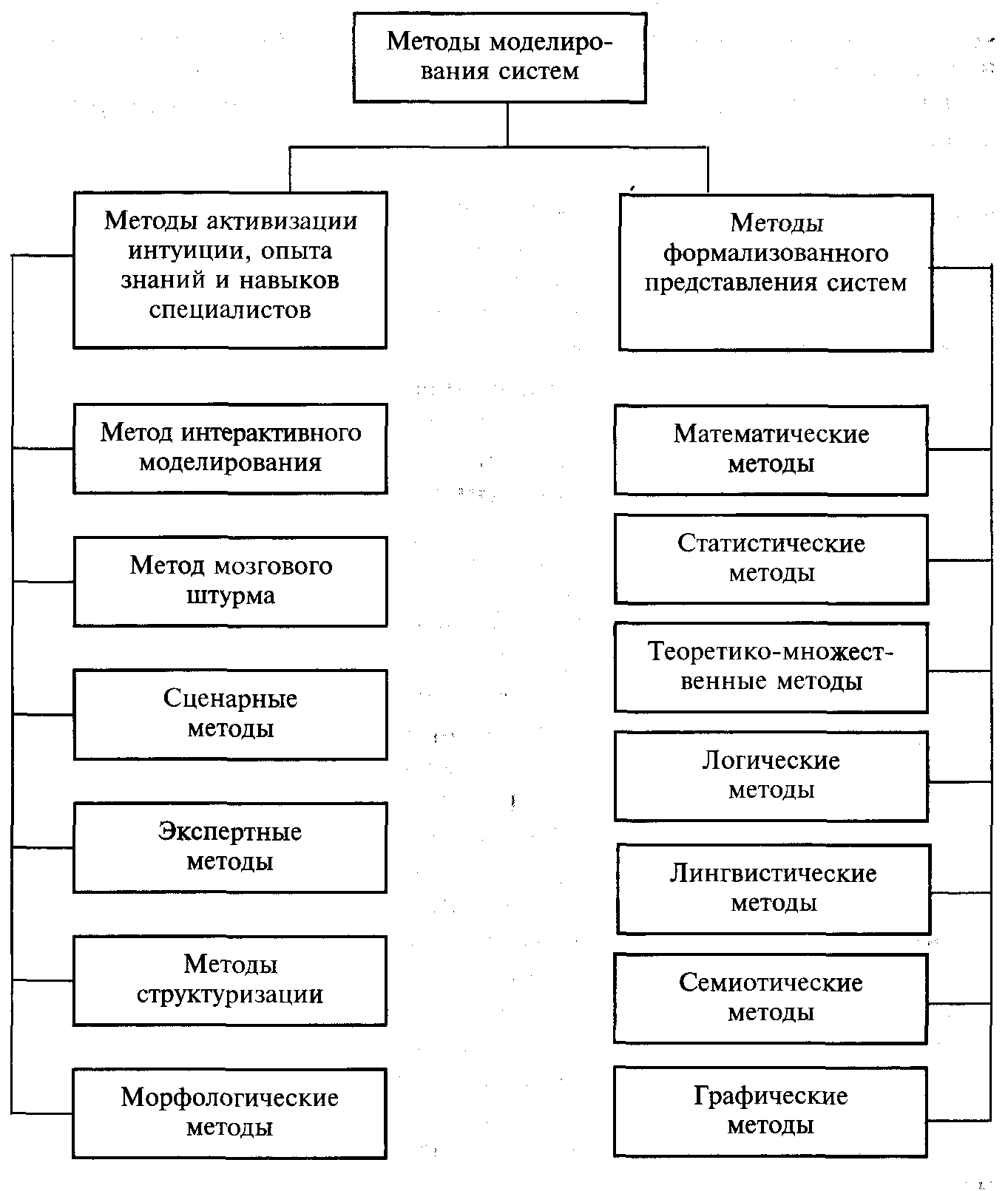
Рис. 2.1.4. Классификация методов моделирования систем

Если разделить шкалу методов примерно посередине (где позиционируются графические методы структуризации), получим два больших класса методов моделирования систем:

1) методы формализованного представления систем;

2) методы активизации интуиции, опыта, знаний и навыков специалистов.

Такое разделение методов полностью согласуется с основной идеей системного анализа, которая заключается в сочетании формализован­ных и неформализованных представлений об исследуемой системе, что помогает в разработке методик, выборе методов постепенной формали­зации, отображения и анализа проблемной ситуации.

Тем не менее строгого разделения между двумя выделенными классами не существует. Можно только говорить о большей или меньшей степени формализованности или, с другой стороны, большей или меньшей опоре на интуицию или здравый смысл.

Приведенная классификация методов моделирования является открытой. Она может развиваться и дополняться конкретными ме­тодами и подходами, аккумулируя опыт, накапливаемый во всех сферах жизнедеятельности.