Динамическая структурная модель

В динамических системах элементы могут вступать в самые раз­нообразные отношения между собой. А поскольку каждый из них способен пребывать во множестве различных состояний, то даже при небольшом числе элементов они могут быть соединены множе­ством различных способов. Построить модель такой системы, пре­дусмотрев изменение состояний одних элементов системы в зави­симости от того, что происходит с другими ее элементами, — очень непростая задача. Тем не менее современная наука выработала не­мало подходов к моделированию такого рода систем. На двух из них, которые стали классическими, остановимся подробнее.

Как и в случае статической структурной модели, динамическая структурная модель представляет собой симбиоз динамической мо­дели «черного ящика» и динамической модели состава. Другими словами, динамическая структурная модель должна увязать в еди­ное целое вход в систему

Х = {x{t)} = {u(t),v(t)}, u(t) € U, v{t) € V,

промежуточные состояния

Ct=[c1(t), c₂(t), ..., c_n(t)], t € [0,T},

и выход

Y = {y(t)}, t € [0,T],

где U — множество управляемых входов u(t);

V — множество неуправляемых входов v(t);

X = U U X — множество всех входов в систему;

Т — горизонт моделирования системы;

C_t — промежуточное состояние системы в момент времени

t € [О, Т];

Y — множество выходов системы.

В зависимости от того, отображаются промежуточные состояния системы строго определенной упорядоченной последовательностью

C_t (t = 0,1, 2, ..., T) или одной неопределенной функцией C= Ф(t,x ͭ) ,

в результате моделирования получают либо динамическую струк­турную модель сетевого типа, либо динамическую структурную мо­дель аналитического типа.

Сетевые динамические модели. В динамической структурной мо­дели сетевого типа для каждой пары соседних состояний системы Сt-1 и Сt (t € [0, 7]) задается управляющее воздействие u(t), которое переводит систему из состояния Сt-1 в состояние Сt. При этом оче­видно, что u(t) на каждом шаге траектории может принимать зна­чения из некоторого множества допустимых управляющих воздей­ствий на этом шаге U ͭ :

u (t) € U ͭ

Таким образом, промежуточное состояние системы в некоторой точке t траектории ее развития записывается следующим образом

C ͭ =F(Ct-1,u(t)), t €[0,T]

Обозначим через C ͭ множество всех состояний системы, в ко­торое можно ее перевести из начального состояния C0=C_H за t ша­гов, используя управляющие воздействия u(t) € U ͭ (t = 0,1,2,..., t).

Множество достижимости C ͭ определяется с помощью следующих рекуррентных соотношений:

C ͭ ={Ct:Ct=f(Ct-1, u(t)); u(t) € U ͭ; t = 0,1, 2,..., t}.

В задании на дальнейшее развитие или первоначальную разра­ботку системы указывается перечень допустимых ее конечных со­стояний, которые должны принадлежать некоторой области

С_T € С‾^Т.

Управление U =< u(1), u(2),..., u(t),..., u(Т) >, состоящее из пошаговых управляющих воздействий, будет допустимым, если оно переводит систему из начального состояния С_H = С₀ в конечное состояние С_k = С_T, удовлетворяющее условию.

Выведем условия допустимости управления. Для этого рассмотрим последний T-й шаг. В силу ограниченности множества U^Т перевести систему в состояние С_T € С^Т можно не из любого состоя­ния С_T-1, а лишь из

С_T-1€ С‾^Т-1,

где С‾^Т-1 - множество, удовлетворяющее условию

Иными словами, чтобы иметь возможность после T-го шага

управления выйти в область допустимых состояний С‾^Т , необходимо

после (Т - 1) шагов находиться в области С‾^Т-1 .

А налогичные множества допустимых состояний С‾ ͭ формируют­ся для всех остальных шагов t= 1,Т-1.

Д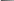 ля достижения цели построения (развития) системы необхо­димо выполнение условий

C ͭ ∩ С‾ ͭ ≠Ø, t = 1,T.

В противном случае цель системы не может быть достигнута.

Для преодоления этого препятствия потребуется либо изменить

цель системы, изменив тем самым С‾^Т , либо расширить область

в озможных управляющих воздействий и ͭ , t = 1,Т (в первую очередь

на тех шагах траектории системы, на которых не выполняется усло­вие.

П усть в результате преодоления (t — 1) шагов система перешла в состояние С_t-1. Тогда множество допустимых управляющих воздей­ствий на t-м шаге определяется следующим образом:

U(t) = {u(t): C_t = f (C_t-1, u(t)) € С‾ ^t }.

Объединяя, можно записать условия управляемого целенаправленного развития системы:

U (t) € U(t) ∩ U(t), t =1, T.

Условия означают, что управление должно быть возможным по его реализуемости и допустимым по обеспечению выхода системы в заданную область конечных состояний.

Таким образом, построение динамической структурной модели системы сетевого типа заключается в формализованном описании траектории ее развития путем задания промежуточных состояний системы и управляющих воздействий, последовательно переводящих систему из начального состояния в конечное, соответствующее цели ее развития.

Поскольку из «начала» в «конец», как правило, существует множество путей, определение траектории развития системы можно вести по различным критериям (минимуму /времени, максимуму эффекта, минимуму затрат и т.п.). Выбор критерия определяется целью моделирования системы.

Такой подход к моделированию динамических систем, как пра­вило, приводит к построению сетевых моделей разных типов (сете­вым графикам, технологическим сетям, сетям Петри и т.п.). Неза­висимо от типа сетевой модели их сущность заключается в том, что они описывают некоторую совокупность логически увязанных ра­бот, выполнение которых должно обеспечить построение некоторой системы (предприятия, дороги, политической партии) или перевода ее в другое состояние, соответствующее новым целям и требовани­ям времени.

Аналитические динамические модели. Если промежуточное со­стояние системы задается одной неопределенной функцией C_t, то для построения динамической структурной модели ее необходимо увязать с входом X и выходом Y системы. Другими словами, необ­ходимо построить отображения

ƞ: С * T→Y;

µ : X * T→C,

что графически можно проиллюстрировать следующим образом:

Аналитически это можно записать так:

y(t) = ƞ(t,Ct); t € [0, T]

C_t = µ(t,x ͭ); t € [0, T]

Конкретизируя множества X, С, Y отображения µ и ƞ, мож­но перейти к различным моделям. Так говорят о дискретных и не­прерывных моделях систем в зависимости от того дискретный или непрерывный интервал [0, T].

Если множества X, С, Y дискретной модели имеют конечное число элементов, то такую систему называют конечным автоматом. Если X, С, Y — линейные пространства, а µ и ƞ — линейные операторы, то система называется линейной. Если к линейной системе дополнительно предъявить требования, состоящие в том, что­бы пространства имели топологическую структуру, а µ и ƞ были бы непрерывными в этой топологии, то попадаем в класс гладких систем.

Конкретизация динамических систем на этом, конечно, не за­канчивается. Приведенные модели, скорее всего, являются отдель­ными примерами реальных систем. В классе моделей динамических систем различают еще стационарные модели, мягкие и жесткие мо­дели, которые находят применение при исследовании конкретных прикладных проблем.