7. Динамические модели

Рассмотренные варианты модели «черного ящика», модели состава и структурной модели называют статиче­скими моделями, что подчеркивает их неподвижность.

Следующий шаг в исследовании системы состоит в том, чтобы понять и описать, как система «работает», выполняя свое предна­значение. Такие модели должны описывать поведение системы, фиксировать изменения, происходящие с течением времени, улав­ливать причинно-следственные связи, адекватно отражать последо­вательность протекаемых в системе процессов и этапность ее разви­тия. Такого рода модели называют динамическими. При исследова­нии конкретной системы необходимо определить направление воз­можных изменений ситуации. Если такой перечень будет исчерпы­вающим, то он характеризует число степеней свободы, а значит, достаточен для описания состояния системы. Как оказалось, дина­мические модели делятся на такие же типы, как статические («чер­ного ящика», состава и «белого ящика»), только элементы этих мо­делей имеют временной характер.

Динамическая модель «черного ящика»

При математическом моделировании динамической системы ее конкретная реализация описывается в виде соответствия между возможными значениями некоторой интегральной характеристики системы с и моментами времени /. Если обозначить через С — множество возможных значений с, а через Т — упорядоченное множество моментов времени t, то построение модели динамиче­ской системы равносильно построению отображения

T→C:c(t)€ C^t,

где С — значение интегральной характеристики в точке t € [0, 7].

В динамической модели «черного ящика» предполагается разбиение входного потока х на две составляющие: и — управляемые входы, v - неуправляемые входы.

Таким образом, она выражается совокупностью двух процессов:

{ X' ={u(t),v(t)}; u(t) €U; v(t) €V;

Y<={y(t)}, y(t)€Y.

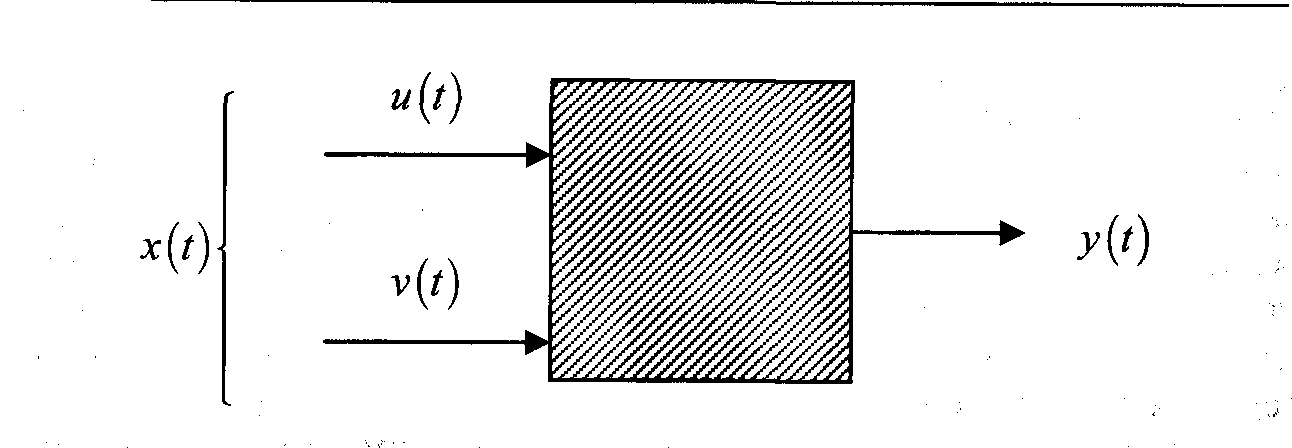
Рис. 2.1.8. Динамическая модель “черного ящика”

Если даже считать y(t) результатом некоторого преобразования Ф процесса x(t), т.е. y(t) = Ф[x(t)], то в модели «черного ящика» предполагается, что это преобразование неизвестно.

Из данного типа моделей в наибольшей мере изучены так назы­ваемые безынерционные системы. Они не учитывают фактора време­ни и работают по схеме «если-то». Например: если воду нагреть до 100 С, то она закипит. Или: если вы правильно авторизовали свою кредитную карту, то банкомат вам сразу выдаст затребованную сумму денег. То есть следствие вступает в силу сразу за причиной.

Определение 1. Динамическая система называется безынерцион­ной, если она мгновенно преобразует вход в выход, т.е. если y(t).

является функцией только x(t) в тот же момент времени.

Поиск неизвестной функции y(t) = Ф(x(t)) осуществляется по­средством наблюдения входов и выходов исследуемой системы. По существу, эта задача о переходе от модели «черного ящика» к моде­ли «белого ящика» по наблюдениям входов и выходов при наличии информации о безынерционности системы.

Однако класс безынерционных систем весьма узок. В экономи­ке такие системы очень большая редкость. Разве только отдельные биржевые операции с некоторой натяжкой можно причислить к классу безинерционных.

При моделировании экономических систем необходимо пом­нить, что в них всегда присутствует задержка и, более того, следст­вие (результат) может проявиться совсем не в том месте, где его ожидали. Таким образом, имея дело с экономическими системами, нужно быть готовым к тому, что последствия могут отстоять от вы­звавшей их причины во времени и пространстве.

Например, если в фирме отдел сбыта пустит на самотек пред­продажное обслуживание и сконцентрирует все свои силы на про­дажах, пострадает отдел гарантийного обслуживания. Но это про­явится не сразу, а спустя определенное время. На лицо проявление следствия «не там и не в то время». Или: для изменения покупа­тельских пристрастий может потребоваться несколько недель рек­ламной кампании, и не обязательно ощутимые перемены начнутся сразу же после ее окончания.

Обратная связь действует по цепочке причинно-следственных связей, образующих замкнутый контур, и требуется время, чтобы его обойти. Чем большей динамической сложностью обладает сис­тема, тем больше нужно времени на то, чтобы сигнал обратной свя­зи пробежал по ее структуре (сети взаимосвязей). Достаточно одной задержки, чтобы обеспечить сильное запаздывание сигнала.

Определение 2. Время, необходимое для того, чтобы сигнал об­ратной связи прошел по всем звеньям системы и вернулся в исход­ную точку, называется памятью системы.

Не только живые системы имеют память. В экономике, напри­мер, это ярко демонстрирует процесс вывода на рынок нового то­вара. Как только на рынке появляется новый товар, пользующийся спросом, сразу находится много желающих его производить. Мно­гие фирмы запускают производство этого товара, и пока существует спрос, наращивают его объемы. Рынок постепенно насыщается, но производители пока этого не ощущают. Когда объем производства превысит некоторое критическое значение, спрос станет падать. Производство товара по определенной инерции еще некоторое вре­мя будет продолжаться. Начнется затоваривание складов готовой продукцией. Предложение сильно превысит спрос. Цена на товар упадет. Многие фирмы прекратят производство этого товара. И та­кая ситуация будет сохраняться до тех пор, пока предложение не упадет до таких значений, что не сможет покрыть существующий спрос. Рынок сразу уловит складывающийся дефицит и отреагирует повышением цены. После этого начнется оживление производства и новый цикл взлета-падения рынка. Так будет продолжаться до тех пор, пока на рынке не останутся несколько производителей, которые либо договорятся между собой, либо интуитивно нащупают квоты производства товара, суммарный объем которых будет соответство­вать требуемому соотношению спроса и предложения.

Точно так же выглядят графики инфляции и дефляции денеж­ного рынка, расцвета и крахов фондового рынка, пополнения и расходования семейного бюджета. Все дело в том, что причину и следствие разделяет задержка во времени. Все это время система «помнит» как она должна отреагировать на причину. На первых порах кажется, что и следствия-то никакого нет. Но со временем эффект проявляется. Введенные в заблуждение (в нашем примере предприниматели) слишком поздно и слишком сильно реагируют на пики спроса и предложения. А во всем виновата уравновешивающая обратная связь, работающая с задержкой во времени.

Рис. 2.1.9. Колебание рынков товаров

В такой ситуации есть два решения. Во-первых, можно сделать более надежным измерение, осуществляя постоянный или перио­дический мониторинг рынка. Во-вторых, следует учитывать раз­ницу во времени и стремиться оказаться там где нужно к тому времени, когда сигнал обратной связи успеет пройти через все звенья системы. Когда понимаешь, как осуществляется процесс, появляется возможность изменить ситуацию в желательном на­правлении.

В очень сложных системах следствие может проявиться спустя очень длительное время. К тому времени, когда оно даст о себе знать, критический порог может миновать и будет уже поздно что-либо исправлять. Особенно наглядно такая опасность просматрива­ется во влиянии промышленных отходов на окружающую среду. То, что мы делаем сейчас, скажется на нашей будущей жизни, когда появятся последствия наших дел. Нашими сегодняшними поступ­ками мы формируем облик будущего.

В облике динамической модели «черного ящика», по существу, ничего не изменится, кроме того, что момент появления выхода у потребуется скорректировать на время задержки ∆, т.е. выход сис­темы примет вид y(t + ∆). Однако основная труд­ность моделирования в том и заключается, чтобы определить вели­чину ∆ и место, в котором появится у. Наилучшим образом это удается в рамках построения так называемых лаговых моделей, кото­рые изучает математическая статистика.