5. Однофакторный дисперсионный анализ

Рассмотрим идеальный вариант – случайные воздействия отсутствуют и необходимо исследовать влияние только одного фактора. Наилучшей оценкой влияния фактора может служить величина, аналогичная дисперсии, характеризующая рассеяние выходной величины _i вокруг некоторого среднего значения. Однако не следует забывать, что в данном случае наблюдается только аналогия с дисперсиями, так как _i – детерминированные величины, поскольку влияющие величины и погрешность восприятия отсутствуют.

Тогда количественная оценка влияния фактора может быть представлена в виде:

²_i = ∑ (_i –y’)²/(N-1),

где N – количество приборов (уровней), каждым из которых проводится одно измерение.

В действительности наблюдается влияние случайных неучтенных величин, которые в совокупности можно обозначить ε. Влияние их можно представить в виде ²_ε. При этом дисперсия выходной величины уже будет определяться не только влиянием фактора х, но и случайной величины ε. Сопоставление влияния этих величин через сопоставление обусловленных ими дисперсий и является основой дисперсионного анализа. Если исследуемый фактор несущественен и дисперсия воспроизводимости, характеризующая один опыт, известна, то общая дисперсия будет в основном определяться дисперсией воспроизводимости. Если же фактор существенен, то можно считать, что

S²₀{y} = ²_x + ²_g.

Таблица 3.1.

i	l=1	l=2	…	l=m	i
1	11	12	…	1m	1
2	21	22	…	2m	2
…	…	…	…	…	…
N	N1	N2	…	Nm	N

Исходя из данного соотношения, можно найти дисперсию, которую обуславливает изучаемый фактор. Обычно дисперсия воспроизводимости ²_ε неизвестна и ее необходимо найти по результатам экспериментальных исследований, поэтому проводят параллельные опыты для каждого уровня варьирования факторов.

Предположим, что исследование объекта проводится одновременно различными приборами с целью уменьшения влияния фактора – прибора на результат исследования (погрешность показаний). Выясним, можно ли систематические погрешности приборов считать одинаковыми.

Пусть приборов будет N (фактор варьируется на N уровнях) и для каждого прибора (уровня) проводится серия из m параллельных опытов. Число опытов при реализации однофакторного дисперсионного анализа будет Nm. Результаты опытов приведены в таблице 3.1.

По результатам исследований для каждого i-го уровня независимой переменной (разновидности прибора) находят среднее значение (предполагаем одинаковую кратность проведения опытов).

y’_i = ∑ y_i1/m.

Разброс значений откликов в фиксированной строке (для конкретного прибора) определяется совокупным действием случайных величин и характеризуется оценкой дисперсии воспроизводимости. Раэброс между средними значениями выходных величин определяется влиянием фактора. Если систематические погрешности приборов одинаковы, то следует ожидать повышенного рассеивания выборочных средних y’_i.

Несмещенная оценка дисперсии воспроизводимости для всей совокупности исследования определяется в виде

S²₀{y} =∑∑(_i1 – y’)²/(Nm – 1),

где y’ = ∑ y_i/N.

Рассмотрим числитель данного выражения Q²₀, введя под скобки –y’_i и +y’_i:

Q²₀ = ∑∑[(_il – y’_i) + (y’_i – y’)]² + ∑∑[(_il – y’_i)² + 2∑∑(_il – y’_i)(y’_i – y’) + +∑∑ (y’_i – y’)².

Рассмотрим отдельно второе слагаемое в правой части выражения Q²₀:

∑∑(_il – y’_i)(y’_i – y’) = ∑(y’_i – y’) ∑(_il – y’_i).

Так как сумма отклонений от среднего в i – ой серии равна нулю

∑(_il – y’_i) = 0, то и второе слагаемое также равно нулю.

Следовательно, полная сумма квадратов отклонений отдельных наблюдений от y’:

Q²₀ = ∑∑[(_il – y’_i)² + ∑∑ (y’_i – y’)² = ∑∑[(_il – y’_i)² + m∑(y’_i – y’)²,

или в сокращенном виде

Q²₀ = Q²_ε + Q²_х,

где

Q²₀ = ∑∑[(_il – y’_i)²; Q²_ε = ∑∑[(_il – y’_i)²;

Q²_х = m∑(y’_i – y’)².

Слагаемое Q²_х представляет сумму квадратов разностей между средними y’_i отдельных серий (строк, приборов) и общей средней y’ по всей совокупности наблюдений и характеризует степень расхождения систематических погрешностей в отдельных приборах. Ее также называют «рассеиванием по факторам».

Слагаемое Q²_ε представляет сумму квадратов разностей между отдельными наблюдениями и средней соответствующей серии y’_i (среднее значение показаний данного прибора) и характеризует «остаточное рассеивание» случайных погрешностей опытов.

Следовательно, полное рассеивание показаний приборов Q²₀ складывается из двух компонент, характеризующих рассеивание между приборами, т.е. различие между их систематическими погрешностями Q²_х и рассеиванием «внутри» приборов (серий), характеризующим одинаковую (на основании предпосылок дисперсионного анализа) для всех приборов вариацию под воздействием случайных величин Q²_ε.

Предположим, что гипотеза равенства систематических погрешностей верна и потому нормальные распределения для всех приборов тождественны, т.е. погрешности имеют одинаковый центр распределения (систематическая погрешность) и дисперсию Q²_ε. Вэтом случае все Nm наблюдений можно рассматривать как выборку из одной и той же нормальной совокупности, а Q²₀/(Nm – 1), как уже отмечалось, является несмещенной оценкой дисперсии Q²_ε по этой выборке. Откуда следует, что отношение Q²₀/ Q²_ε , будет следовать распределению ² с (Nm – 1) степенями свободы.

Однако средние по группам (приборам) y’_i также, в соответствии с предположением, нормально распределены с дисперсией Q²_ε/m каждая и независимы друг от друга. Поэтому

∑(y’_i – y’)²/(N – 1) = Q²_х/m(N – 1)

является несмещенной выборочной характеристикой дисперсии Q²_ε/m, полученной на основании N наблюдений величины y’_i. В результате можно заключить, что величина

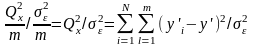
распределена по закону ² с (N – 1) степенями свободы.

Сумма квадратов отклонений от среднего в каждой серии, отнесенная к дисперсии

∑(_il – y’_i)²/²_ε,

также распределена по закону ² с (m – 1) степенями свободы.

Согласно свойству композиции для Nсерий (приборов), компонента

Q²_ε/²_ε =∑∑(_il – y’_i)²/ ²_ε

также распределена по закону ² c N(m – 1) является также оценкой параметра ²_ε.

Из изложенного следует, что в случае равенства систематических погрешностей приборов (несущественности влияния исследуемого фактора) существуют три несмещенные оценки ²_ε. Отношение двух однородных оценок дисперсий

F_p = [Q²_х/(N – 1)]/[ Q²_ε /N(m – 1)]

будет следовать F – распределению с (N – 1) и N(m – 1) степенями свободы. Задаваясь  уровнем значимости , на основании таблицы F-распределения, можно установить соответствующий  предел, так что

P(F_p>F_T) = /100.

Рассмотрим случай, когда исследуемый фактор существенен, т.е. гипотеза о равенстве систематических погрешностей (центров распределения случайных погрешностей) неверна, но параметр ²_ε во всех N совокупностях один и тот же. Изменение центров построчных распределений, т.е. замена _il на _il – с_i (где с_i – систематическая составляющая погрешности i-го прибора) не изменит значения Q²_ε, которое по прежнему распределено по закону ² c N(m – 1) степенями свободы, а Q²_ε /N(m – 1) остается несмещенной оценкой ²_ε. Однако числитель выражения (3.1.) именно учитывает расхождение между центрами распределения с_i и имеет тенденцию к возрастанию при увеличении расхождения между систематическими составляющими. Поэтому правило проверки правильности выдвинутой гипотезы можно представить в следующем виде: гипотеза с₁ = с₂ =  = с_N принимается, если F_T >F_P, и отбрасывается, если F_P >F_T. Схема однофакторного дисперсионного анализа может быть представлена в виде табл. 3.2.