
1 Метод наименьших квадратов
Пусть имеется N
пар наблюдений (xi,yi),
причем xi
— фиксированные значения входной
величины. Этому набору соответствует
некоторое поле корреляции. Необходимо
подобрать линию регрессии вида
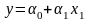 ,
которая бы наилучшим образом описывала
поведение объекта. Так как по
экспериментальным данным (значениям
,
которая бы наилучшим образом описывала
поведение объекта. Так как по
экспериментальным данным (значениям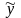 )
определяются коэффициенты модели, то
они будут случайными величинами.
)
определяются коэффициенты модели, то
они будут случайными величинами.
Для оценки
коэффициентов регрессии
 и
и
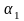 используется метод наименьших квадратов
(МНК),
который позволяет
минимизировать сумму квадратов разности
отклонений экспериментальных данных
i
и расчетных значений, полученных на
основании уравнения регрессии
используется метод наименьших квадратов
(МНК),
который позволяет
минимизировать сумму квадратов разности
отклонений экспериментальных данных
i
и расчетных значений, полученных на
основании уравнения регрессии
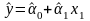 .
МНК заключается в минимизации функции
.
МНК заключается в минимизации функции
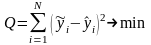
Для линейной парной зависимости имеем
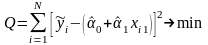
При нахождении
оценок коэффициентов, удовлетворяющих
данному условию, необходимо взять
частные производные
 и приравнять их к нулю. Получим систему
уравнений, называемую системой нормальных
уравнений. Число этих уравнений
соответствует числу неизвестных. Введем
фиктивную переменную
и приравнять их к нулю. Получим систему
уравнений, называемую системой нормальных
уравнений. Число этих уравнений
соответствует числу неизвестных. Введем
фиктивную переменную
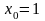 и умножим на нее
и умножим на нее
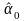 .
Получим следующую систему нормальных
уравнений:
.
Получим следующую систему нормальных
уравнений:
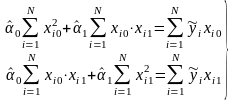
Представленная в данном виде система нормальных уравнений имеет три особенности:
1) в правой системы
под знаком суммы расположены произведения,
полученные в результате последовательного
умножения совокупности выходных величин
на совокупность j-й
входной величины (введение
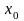 позволяет найти оценку коэффициента
,
называемого свободным членом);
позволяет найти оценку коэффициента
,
называемого свободным членом);
2) на диагонали левых частей уравнений под знаком суммы последовательно стоят квадраты независимых переменных:
3) по отношению к диагонали в левой части наблюдается симметрия.
Оценки коэффициентов уравнения регрессии, удовлетворяющих методу наименьших квадратов, можно найти из соотношений:
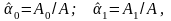
где
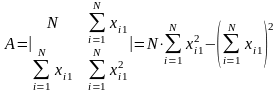 ─
─
─главный определитель системы при условии, что , называемая фиктивной переменной, тождественно равно единице;

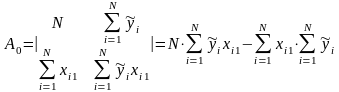
являются дополнениями.
Следовательно,
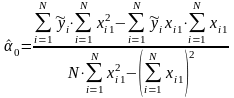
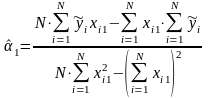
Нахождение оценок
методом наименьших квадратов базировалось
на предположении, что условное
математическое ожидание Y
при данном х
линейно и зависит от х.
Графически математическая модель
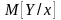 представлена на рис.1.3. погрешность
измерения предполагается связанной с
измеряемой величиной
представлена на рис.1.3. погрешность
измерения предполагается связанной с
измеряемой величиной
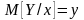 и распределена по нормальному закону.
Следовательно полученное значение
выходной величины исследуемого объекта
будет случайной величиной, тоже
распределенной по нормальному закону.
и распределена по нормальному закону.
Следовательно полученное значение
выходной величины исследуемого объекта
будет случайной величиной, тоже
распределенной по нормальному закону.
В связи с этим может быть выдвинуто множество гипотез о конкретном виде модели (значениях коэффициентов), не противоречащих опытным данным. Задача состоит в выборе модели, наилучшим образом описывающей поведение объекта. Для этого воспользуемся методом максимального правдоподобия, по которому выбирается такая гипотеза, согласно которой вероятность получения в процессе измерения фактически наблюдаемых величин была бы максимальной. Если при каждом х значения Y распределены по нормальному закону со средним на прямой регрессии М [Y/x]=a0+a1x1(см. рис. 1.3), то условная плотность вероятности Yi

Если имеем N выборочных точек, где проводился эксперимент, то функция правдоподобия будет равна произведению условных вероятностей выходных величин, т. е.
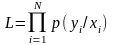
Прежде, чем исследовать функцию правдоподобия на максимум, прологарифмируем ее:
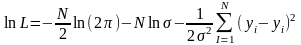 (1.2)
(1.2)
Для получения оценок максимального правдоподобия а0мп и a1мп необходимо подставить M[Yi /xi]=yi=a0+a1x1 и взять частные производные lnL по а0 и а1 и приравнять их нулю. Из рассмотрения выражения (1.2) можно сделать вывод, что оно будет стремиться к максимуму, когда последнее слагаемое в правой части будет стремиться к минимуму. Поэтому необходимо исследовать условия, обеспечивающие минимизацию
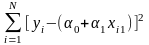 .
.
Данное условие совпадает с условием МНК. Следовательно, метод наименьших квадратов является частным случаем метода максимума правдоподобия при нормальном законе распределения. Оценки коэффициентов, найденные на основании МНК, будут несмещенными, состоятельными и асимптотически нормальными. При этом предполагалось, что только выходная величина исследуемого объекта искажается погрешностью измерения.
В
случае, когда и входная величина х
имеет погрешность измерения (или просто
является случайной величиной), то кроме
минимизации отклонений опытных данных
от линии регрессии параллельно
направлению Оу возможна минимизация
в направлении, параллельном Оy, что
приведет к другой линии регрессии М
[X/Y
= у] =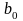 +
+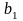 y,
причем коэффициенты
и
нельзя получить простым обращением
ранее полученных коэффициентов
и
.
Для их
получения необходимо в определителях
А, А0
и A1
взаимно поменять х и у и получить
определители В,
B0
и B1,
а затем уже воспользоваться известным
алгоритмом. Таким образом, в случае,
если х и у представляют собой двумерную
величину, то существуют две регрессии
— прямая М [Y
/X = х] и обратная М [Х/Y
= у], пересекающиеся в центре тяжести,
т. е. в точке с координатами
y,
причем коэффициенты
и
нельзя получить простым обращением
ранее полученных коэффициентов
и
.
Для их
получения необходимо в определителях
А, А0
и A1
взаимно поменять х и у и получить
определители В,
B0
и B1,
а затем уже воспользоваться известным
алгоритмом. Таким образом, в случае,
если х и у представляют собой двумерную
величину, то существуют две регрессии
— прямая М [Y
/X = х] и обратная М [Х/Y
= у], пересекающиеся в центре тяжести,
т. е. в точке с координатами
 ,
и образующие некоторый угол между
собой.
,
и образующие некоторый угол между
собой.
В случае предполагаемой линейной зависимости степень тесноты этой связи может быть количественно определена коэффициентом корреляции, выборочное значение которого определяется выражением
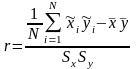 (1.3)
(1.3)
Формально коэффициент корреляции может быть вычислен для любой двумерной системы наблюдений. Однако для совместного нормального распределения случайных величин Х и Y коэффициент корреляции имеет четкий смысл, характеризуя степень тесности связи между ними.
Если |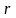 |
= 1, то это подтверждает функциональную
(не статическую) линейную зависимость
между исследуемыми величинами, а
=0, что свидетельствует об их полной
независимости. Однако такое рассуждение
при Если
=0 возможно только в том случае, если
есть полная уверенность, что зависимость
линейна. Если такой уверенности нет,
то при
=0 можно утверждать, что величины
некоррелированы, а уже после детального
статистического анализа говорить об
их независимости.
|
= 1, то это подтверждает функциональную
(не статическую) линейную зависимость
между исследуемыми величинами, а
=0, что свидетельствует об их полной
независимости. Однако такое рассуждение
при Если
=0 возможно только в том случае, если
есть полная уверенность, что зависимость
линейна. Если такой уверенности нет,
то при
=0 можно утверждать, что величины
некоррелированы, а уже после детального
статистического анализа говорить об
их независимости.
Коэффициент корреляции определяет угол наклона линии регрессии, или значение оценки коэффициента .
В ранее полученном соотношении для примем, что входная величина случайна, т. е.
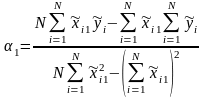
Разделим числитель и знаменатель на N2 и воспользуемся соотношениями.
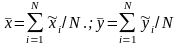
Тогда
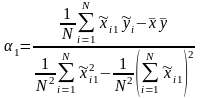 (1.4)
(1.4)
Рассмотрим выражение
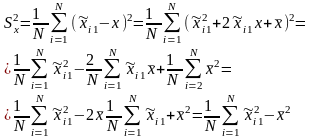
сопоставим его со знаменателем выражения (1.4) и, приняв во внимание выражение (1.3), получим
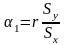
Введем геометрическую
характеристику концентрации точек
корреляционного поля
 около
своего центра тяжести
около
своего центра тяжести
 .
Для случая
совместного нормального распределения
величин Х и Y удобной характеристикой
является эллипс рассеяния.
Его уравнение имеет вид [3]
.
Для случая
совместного нормального распределения
величин Х и Y удобной характеристикой
является эллипс рассеяния.
Его уравнение имеет вид [3]
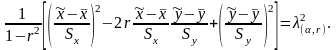
где 2(a,r)— 100 %-ная точка 2- распределения с двумя степенями свободы, и показывает, что 100 (1 — ) % точек поля корреляции будут «накрыты» эллипсом.
Эллипс рассеяния
непосредственно связан с регрессионными
прямыми, которые являются его диаметрами»
сопряженными с координатными осями.
Так, для проведения регрессионной
прямой
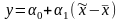 следует построить две вертикальные
прямые KL
и PD,
касательные к эллипсу и соединить
точки касания. Для построения обратной
регрессионной прямой
следует построить две вертикальные
прямые KL
и PD,
касательные к эллипсу и соединить
точки касания. Для построения обратной
регрессионной прямой
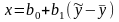 необходимо соединить точки касания
горизонтальных прямых КР
и LD
с эллипсом. Чем больше разброс данных
(чем больше «размыто» корреляционное
поле), тем сильнее эти прямые будут
отличаться (расходиться). Эту зависимость
можно выразить соотношением [3]
необходимо соединить точки касания
горизонтальных прямых КР
и LD
с эллипсом. Чем больше разброс данных
(чем больше «размыто» корреляционное
поле), тем сильнее эти прямые будут
отличаться (расходиться). Эту зависимость
можно выразить соотношением [3]
 (1.5)
(1.5)
где — острый угол, отсчитываемый от линии М [Y/X = х] к линии М [X/Y = у] с обычным правилом знаков (на рис. 1.4 угол отрицательный).
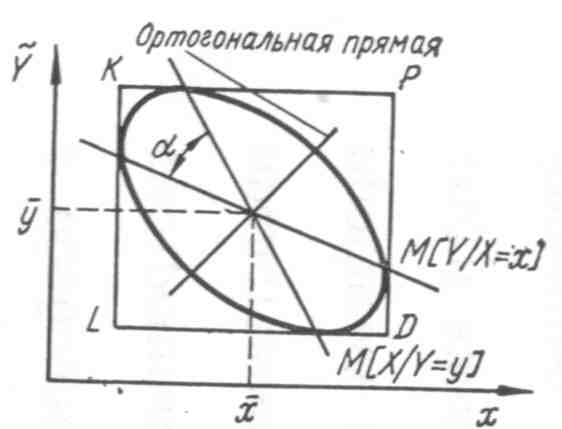
рис. 1.4. Эллипс рассеяния и линии прямой и обратной регрессии
Из выражения (1.5)
следует, что линия обратной регрессии
более круто наклонена к горизонтальной
оси. При отсутствии корреляционной
связи
 и
tg
и
tg линии будут взаимно перпендикулярны.
линии будут взаимно перпендикулярны.
Наличие двух линий регрессии (прямой и обратной) во многих практических случаях является неудобным — возникает необходимость определить такую одну линию, которая бы представляла истинное соотношение между входной и выходной величинами. Такую линию можно получить, если свести к минимуму суммы квадратов расстояний от экспериментальных точек до этой линии, измеряемых в направлении перпендикуляров, опущенных из этих точек на данную линию. Полученная таким образом прямая регрессии называется ортогональной. Однако закон связи между величинами при этом существенно зависит от шкал измерения по координатным осям (масштаба по осям). При различных масштабах по осям нарушается ортогональность. Данный недостаток отсутствует только в том случае, когда входная и выходная величины исследуемого объекта однородны. Понятие ортогональной регрессии также связано с эллипсом рассеяния — она является одной из главных осей эллипса.
