
4. Дробный факторный эксперимент
дробных факторных экспериментов (ДФЭ), представляющих дробные реплики полного факторного эксперимента. Если ПФЭ наблюдения производятся во всех вершинах N─мерного гиперкуба, то при использовании дробных реплик наблюдения проводятся в некоторых из них.
Рассмотрим пример построения дробной реплики, предполагая вначале, что эффекты взаимодействий отсутствует, т. е. модель имеет вид:

При таком виде
зависимости неизвестными являются
четыре коэффициента, для определения
которых достаточно, как минимум, четыре
опыта. Рассмотрим матрицу ПФЭ типа 23
(табл. 2.6). Для оценки коэффициентов

 достаточно четырех опытов (строк). Можно
ли для этой цели выбрать первые четыре
строки? Очевидно нет, так как видно, что
в них
достаточно четырех опытов (строк). Можно
ли для этой цели выбрать первые четыре
строки? Очевидно нет, так как видно, что
в них
 находится только на нижнем уровне и
нельзя получить информации о влиянии
фактора
на выходную
величину. То же можно сказать и о нижних
четырех строках, где фактор
находится только на верхнем уровне.
Можно попытаться выбрать только четные
или нечетные строки полной матрицы
планирования, но результат будет
неудачным. Выберем строки 5, 2, 3, 8 и
построим матрицу плана
находится только на нижнем уровне и
нельзя получить информации о влиянии
фактора
на выходную
величину. То же можно сказать и о нижних
четырех строках, где фактор
находится только на верхнем уровне.
Можно попытаться выбрать только четные
или нечетные строки полной матрицы
планирования, но результат будет
неудачным. Выберем строки 5, 2, 3, 8 и
построим матрицу плана
 ,
,
в которой первые два столбца являются матрицей плана двухфакторного эксперимента вида 22. Следовательно, число опытов в данном плане будет N=22=23—1, или N =23•2─1. Построенная таким образом матрица обладает тремя свойствами: ортогональностью, нормировкой и симметричностью. Но раз матрица плана обладает данными свойствами, то, следовательно, она выбрана не произвольным образом, а по какому-то расчету. Показатель степени в выражении для числа опытов (3-1) показывает дробность матрицы плана ПФЭ N=23, т.е. дробная матрица планирования составляет полуреплику плана ПФЭ. Если сопоставить матрицу Х дробного факторного эксперимента 23─1 и ПФЭ 23, то можно заметить, что переменная в точках плана удовлетворяет уравнению
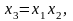
которое имеет свой определенный смысл и называется генерирующим соотношением (ГС).
Таким образом, дробным факторным экспериментом ДФЭ называется эксперимент, реализующий строго определенную часть ПФЭ. Матрицу, получаемую при ДФЭ, называют дробной матрицей планирования (ДМП). Число строк ДМП в общем случае определяется соотношением
N == 2n-p,
где п — число линейных факторов; р — показатель дробности.
Для (п - р) факторов, условно называемых основными, строится матрица полного факторного эксперимента, а для р факторов, называемых дополнительными, уровни варьирования в опытах выбираются на основании генерирующего соотношения. Генерирующее соотношение — это формальное равенство, показывающее, знаки каких основных переменных, стоящих в правой части равенства, необходимо перемножить для получения знака дополнительного фактора (уровня варьирования), чтобы ДМП оказалась ортогональной, нормированной и симметричной.
Исходные данные для решения данной задачи занесём в таблицу.
Три фактора , , являются основными. , .
Регрессионную зависимость необходимо определять в следующем
виде:
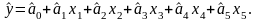
Первым этапом обработки результатов измерений является расчёт критерия Кохрена:
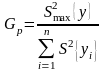 ,
,
где
 - сумма дисперсий во всех точках плана.
- сумма дисперсий во всех точках плана.
Затем расчётное
значение сравнивается с табличным

Так как
 ,
то опыт воспроизводим.
,
то опыт воспроизводим.
Далее рассчитываются коэффициенты регрессионной зависимости:
 ;
;

Тогда регрессионная зависимость будет иметь вид:

Найдём теоретические
значения
 для
каждого из экспериментов и занесём
полученные значения в таблицу.
Относительную ошибку
для
каждого из экспериментов и занесём
полученные значения в таблицу.
Относительную ошибку подсчитаем для каждого из x
экспериментов по формуле:
подсчитаем для каждого из x
экспериментов по формуле:
 .
.
Следующим этапом после определения коэффициентов регрессионной зависимости является оценка их значимости:
 ,
где:
,
где:
 - оценка дисперсии
k-го
коэффициента,
- оценка дисперсии
k-го
коэффициента,
 - дисперсия
воспроизводимости.
- дисперсия
воспроизводимости.
Если
 ,
то данный коэффициент остаётся в
регрессионной зависимости. В противном
случае он исключается.
,
то данный коэффициент остаётся в
регрессионной зависимости. В противном
случае он исключается.
 -
табличное значение коэффициента
значимости (выбирается в зависимости
от степени свободы).
-
табличное значение коэффициента
значимости (выбирается в зависимости
от степени свободы).
=4,3.
В результате преобразований и подсчётов получим:
 =390,4;
=390,4;
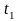 =11,5;
=11,5;
 =4,8;
=4,8;
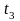 =14,4;
=14,4;
 =7,7;
=7,7;
 =9,6.
=9,6.
В итоге, все шесть коэффициентов являются значимыми.
Заключительным этапом является проверка адекватности модели по критерию Фишера. Расчётное значение критерия Фишера определяется по формуле и сравнивается с табличным значением:
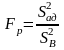 ,
где
,
где
 -
дисперсия адекватности,
-
дисперсия адекватности,
l – число значимых факторов.
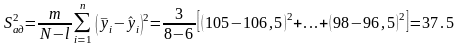
=37,5/1,66=22,6
<
 модель адекватна.
модель адекватна.
