§ 5. Экономические задачи, содержащие вектора и прямые

Наиболее простыми задачами данного раздела являются задачи на нахождение прибыли предприятия, выпускающего несколько видов продукции. Рассмотрим конкретный пример.

Пример 1. Предприятие выпускает три вида продукции , и , в количестве 15, 25 и 45 штук, реализуемых по ценам 30, 45 и 50 усл. ед. соответственно. Найти 1) выручку предприятия от реализации продукции и ее изменение при изменении цен продукции , и соответственно на +5, -3 и -4 усл. ед. 2) при условии необходимости получения прибыли в размере 12 тыс. усл. ед., фиксированном выпуске продукции и невозможности изменить установленную цену, указать выпуск продукции, необходимый для получения указанной прибыли.

Решение:

1) Для нахождения первоначальной выручки предприятия необходимо вычислить скалярное произведение векторов выпуска и цены реализации:

(усл. ед.)

При изменении цены изменение выручки составит

,

т.е. выручка сократится на 180 усл. ед. и составит, соответственно, 3645 (усл. ед.).

2) Обозначим выпуск продукции через , а продукции через . Если цена на все виды продукции и выпуск первой продукции фиксированы, то условие необходимости получения прибыли в размере 12 тыс. усл. ед. выражается следующим образом:

, или

, т.е.

Таким образом, для получения указанной прибыли при заданных условиях необходимо, чтобы вектор выпуска продукции имел следующий вид:

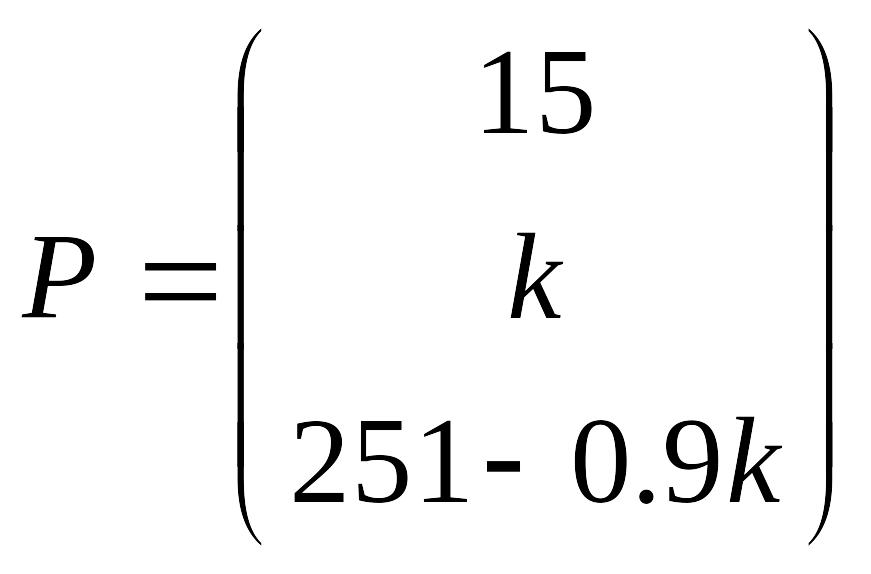
где - некоторый параметр производства.

Рассмотрим некоторые простейшие линейные экономические зависимости и основные понятия, связанные с ними.

При производстве единиц любой продукции совокупные издержки (затраты) состоят из двух слагаемых — постоянных (фиксированных) и переменных издержек:

Здесь постоянные издержки — это издержки, не зависящие от числа единиц произведенной продукции. Они включают в себя амортизацию, аренду помещения, проценты по займам и т.п. Переменные издержки V — это издержки, напрямую зависящие от количества произведенной продукции. Они включают в себя стоимость сырья, рабочей силы и т.п.

В простейшем случае переменные издержки прямо пропорциональны — количеству произведенной продукции и коэффициент пропорциональности — это переменные затраты по производству одной единицы продукции. Если при этом обозначить через фиксированные затраты, то получится урав­нение, которое называется линейной моделью издержек:

Совокупный доход, или выручка, , получаемый предприятием от продажи единиц продукции, определяется формулой

где — цена единицы товара.

Если произведено и продано единиц продукции, то прибыль определяется формулой

Точка, в которой прибыль обращается в нуль, называется точкой безубыточ­ности.

Количество товара, которое покупа­тели приобретут на рынке, зависит от цены на этот товар. Соотношение между ценой и количеством купленного товара называется функцией или законом спроса. Количество товара, которое производители выставят на продажу, также зависит от цены на этот товар. Соотношение между ценой и ко­личеством товара, выставленного на продажу, называется функцией или законом предложения.

В простейшем случае эти функции ли­нейны. В ряде учебников и задачников закон спроса традиционно обозначается через D, закон предложения — через S, при этом — количество товара, — цена на этот товар.

Уравнение спроса можно составить, если заданы две точки, лежащие на его графике. Для этого нужно использовать уравнение прямой, проходящей через две заданные точки (см. теорию §4 на стр. ?)

Точка пересечения кривых (в нашем случае – прямых) спроса и предложения называется точкой рыночного равновесия. Соответственно, называется равновес­ной ценой, a — равновесным количеством (объемом продаж).

Очень часто правительство вводит налог на товар или предоставляет субсидию s, чтобы население могло приобрести этот товар по разумной цене. При использовании линейных моделей предполагается, что спрос оп­ределяется только ценой товара на рынке, а предложение — только ценой, получаемой поставщиками. Таким образом, при введении налога или субсидии уравнение спроса D не изменится, а график функции предложения поднимется на t единиц вверх (S') (см. рис 1) или опустится на s единиц вниз (S') (см. рис. 2).

Вместо субсидии иногда вводится минимальная цена. В этом случае пра­вительство скупает излишек продук­ции, равный (см. рис. 3).

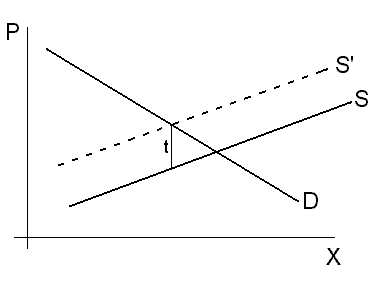
Рис. 1.

Рис. 2.

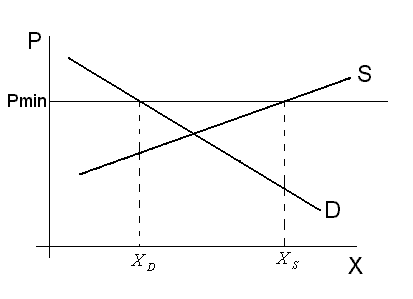
Рис. 3.

Некоторые налоги, например НДС (налог на добавленную стоимость), про­порциональны цене. В этом случае ос­тается той же точка пересечения графи­ка предложения с осью ОХ и меняется лишь угол наклона графика к оси ОХ. Доход правительства при этом будет равен произведению доли налога на координаты новой точки рыночного равновесия:

Рассмотрим несколько конкретных примеров.

Пример 2. Законы спроса и предложения имеют следующий вид:

,

а) какая субсидия приведет к увеличению равновесного объема продаж на 2 единицы?

б) какой налог приведет к снижению равновесного объема продаж на 3 единицы?

Решение:

а) вычислим точку рыночного равновесия. Для этого объединим уравнения спроса и предложения в систему:

,

решая которую получаем: , .

По условию, после введения субсидии новая точка равновесного объема продаж будет . Поскольку уравнение спроса остается неизменным, то , т.е. .

Построим прямую, параллельную закону предложения и проходящую через новую точку равновесия . Это будет прямая (см. теорию §4 на стр. ?)

,

причем параметр найдем из условия, что она проходит через точку , т.е.

,

и, окончательно, новый закон предложения имеет вид

.

Очевидно, что относительно оси прямая предложения сместилась вниз на 12 единиц (разность свободных членов старой и новой прямых ) – это и есть величина искомой субсидии.

б) Исходная точка рыночного равновесия была найдена ранее: , .

По условию, после введения налога новая точка равновесного объема продаж будет . Поскольку уравнение спроса остается неизменным, то , т.е. .

Построим прямую, параллельную закону предложения и проходящую через новую точку равновесия . Это будет прямая

,

причем параметр найдем из условия, что она проходит через точку , т.е.

,

и, окончательно, новый закон предложения имеет вид

.

Очевидно, что относительно оси прямая предложения сместилась вверх на 18 единиц (разность свободных членов старой и новой прямых ) – это и есть величина искомого налога.

Пример 3. Законы спроса и предложения имеют следующий вид:

,

а) правительство вводит налог, равный 25 %. Найти новую точку равновесия и доход правительства.

б) установлена минимальная цена, равная 7,5 усл. ед. Сколько потратит правительство на скупку излишка продукции?

Решение:

а) вычислим точку рыночного равновесия. Для этого объединим уравнения спроса и предложения в систему:

,

решая которую получаем: , .

При введении налога в 25 %, рыночная цена товара будет составлять 125 % от первоначальной стоимости, при этом 100 % (или 4/5 части) получат производители и 25 % (или 1/5 часть) получит государство. По условию, уравнение спроса остается неизменным. Неизменной останется также и точка пересечения графи­ка предложения с осью ОХ. Поскольку изменится угол наклона графика к оси ОХ с коэффициентом пропорциональности, равным доле дохода производителей, новый закон предложения будет иметь вид

.

Вычислим новую точку рыночного равновесия. Для этого объединим уравнения спроса и новое уравнение предложения в систему:

,

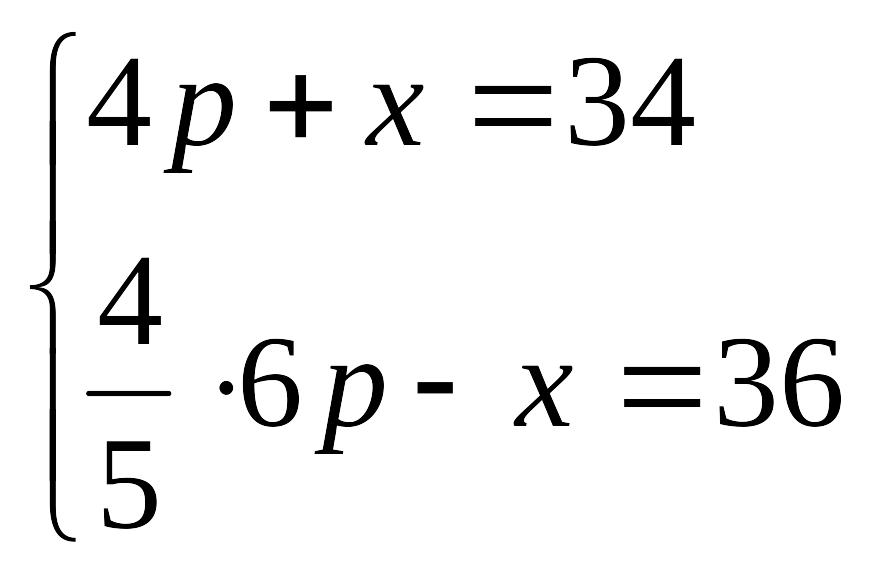решая которую получаем: , .

Тогда доход правительства (см. теорию на стр. ?) равен

(усл. ед.)

б) При условии, что минимальная цена равна 7,5 усл. ед., из закона спроса

,

а из закона предложения

.

Излишек продукции составит единиц и при условии, что цена составляет 7,5 усл. ед., правительство потратит на покупку этого излишка усл. ед.

Пример 4. Законы спроса и предложения имеют следующий вид:

,

_{Какой налог должно ввести правительство, если хочет получить доход, равный 216 усл. ед.?}

_{Решение.}

Пусть доля дохода правительства равна . Тогда доля дохода производителя равна . По условию, , где - точка равновесия, найденная из системы

Следовательно, , при этом из первого уравнения , тогда второе уравнение можно переписать в виде

Выполняя элементарные преобразования

приходим к квадратному уравнению вида

решая которое получаем , . Тогда , . Тогда , . Значение является посторонним корнем, т.к. введение налога такой величины невозможно с экономической точки зрения. Следовательно, доля дохода правительства равна , и, следовательно, величина введенного налога составляет 12 %.