2.2. Лемма Ахо.

Какова бы ни была матрица 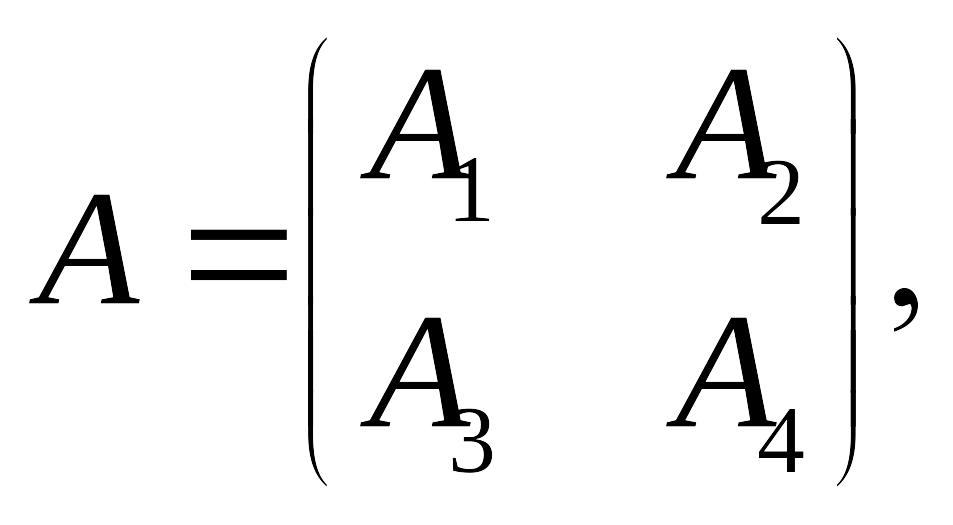такая, что существуют обратные матрицы к матрицам и , обратная матрица к исходной будет иметь вид:

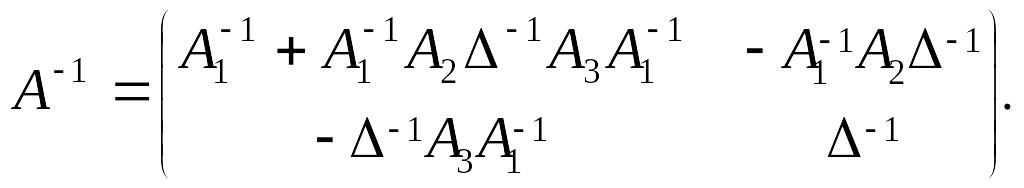
Применим данную лемму к примеру 6. Матрица, которую мы рассматриваем, имеет вид

,

т.е. , , , . Тогда (это предлагается вычислить самостоятельно)

, ,

,

,

,

, , (1)

,

, (2)

, (3)

(4)

Объединяя результаты (1), (2), (3) и (4), получаем:

.

По числу арифметических действий этот способ гораздо более экономичный, чем метод Гаусса, хотя его формула выглядит более громоздкой и трудной для запоминания.

2.3. Если есть компьютер.

Вполне естественно, что для реализации методов обратной матрицы, Гаусса и Ахо существует множество пакетов программ для различных операционных систем. Большая часть из них являются лицензионными и продаются официально. Однако достаточно часто возникает ситуация, когда нет необходимости в целом фундаментальном пакете. При этом языки программирования высокого уровня требуют неоправданных затрат, в том числе и интеллектуальных. В этом случае можно воспользоваться одним из стандартных математических пакетов, реализованных как большой научный калькулятор, например MathCad.

Одна из существующих версий – Mathcad 2000 Professional Русская версия – распространена достаточно широко и вполне удобна для использования, как, впрочем, и все остальные менее популярные версии.

Ваш рабочий экран будет при этом выглядеть следующим образом:

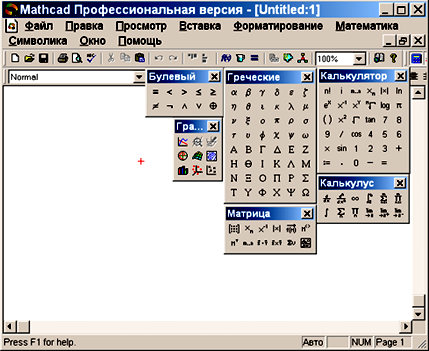
На размещенных справа панелях содержатся все необходимые значки – матрицы, суммы, интегралы, вызов двухмерных и трехмерных графиков, гистограмм, а также многое другое – достаточно лишь щелкнуть мышкой нужный значок. Подробности можно узнать запросив помощь по клавише F1 или заглянув в доступную литературу.

Два обязательных правила, которые необходимо помнить:

1. значения, которые Вы заносите в компьютер, записываются через знак “ 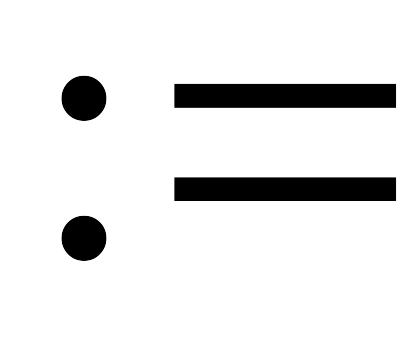” (он есть внизу на панели “Калькулятор” или просто нажатием клавиш “:” и “=”), а те значения, которые Вам хотелось бы получить от компьютера, запрашиваются через знак “ ”;

2. MathCad без проблем работает только с латинским алфавитом, не переходите на русскую раскладку клавиатуры.

Например, получить определитель, вычисленный в примере 1 данного параграфа, можно выполнив следующие действия:

1) набрать на клавиатуре А : =

2) на панели “Матрица” выбрать значок, обозначающий матрицу (в левом верхнем углу)

3) в появившемся окошке указать, что наша матрица имеет 4 строки и 4 столбца:

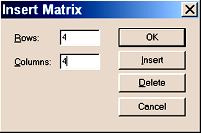
после чего нажать “ОК”

4) заполнить появившуюся сетку необходимыми числами

5) теперь, если под этой матрицей поставить значок “| |” (на панели “Матрица” он в верхнем ряду, четвертый слева), вписать в него букву А, а затем поставить обычный знак равенства “=”, мы мгновенно получим значение определителя.

Если все сделано правильно, экран будет выглядеть следующим образом:

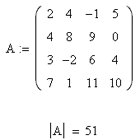
Совершенно аналогично можно найти и обратную матрицу. При этом первые 4 пункта приведенного алгоритма останутся без изменения, а 5-й будет выглядеть так:

5) теперь, если поставить значок “Х^-1” (на панели “Матрица” он в верхнем ряду, третий слева), вписать в него букву А, а затем поставить обычный знак равенства “=”, мы мгновенно получим значение обратной матрицы.

Если продолжить пример, для которого мы только что запрашивали определитель, то экран будет выглядеть следующим образом:

Естественно, что пример 5 данного параграфа в MathCade выглядит намного проще и решается быстрее. Для этого всего лишь достаточно заполнить матрицы и (мы уже умеем это делать), а затем записать следующее:

1. В : =

2. поставить значок “Х^-1”

3. вписать в него 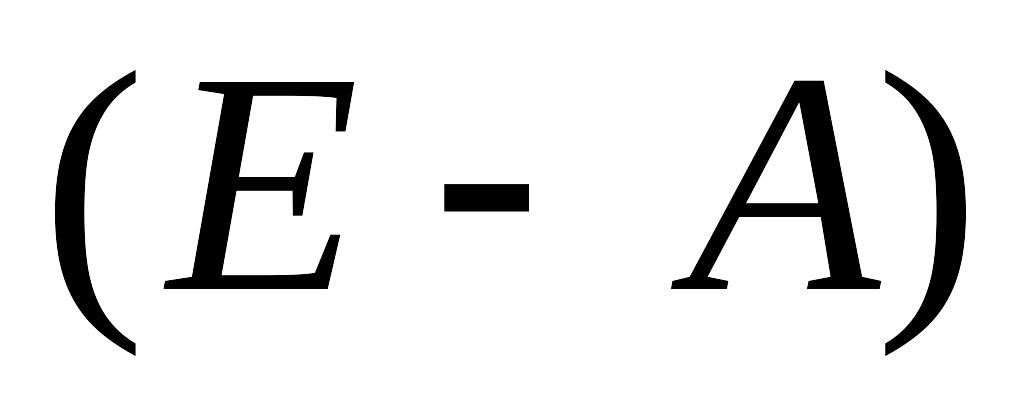- скобки при этом обычные, с клавиатуры

4. строкой ниже записать В =.

Если все сделано правильно, экран будет выглядеть следующим образом:

Одна из экономических задач, относящаяся к многоотраслевой модели Леонтьева, уже была разобрана нами в примере 5 (см. пункт 2.1) данного параграфа. Чуть позже (в пункте 2.4) мы еще раз вернемся к этой модели.

Но иногда системы линейных алгебраических уравнений возникают в достаточно простых задачах, не имеющих строгой привязки к каким-либо экономическим теориям. Рассмотрим следующий пример⁵:

Пример 7. Фирмой было выделено 236 тыс. усл. ед. для покупки 29 предметов для оборудования офиса: несколько компьютеров по цене 20 тыс. усл. ед. за компьютер, офисных столов по 8,5 тыс. усл. ед. за стол и стульев по 1,5 тыс. усл. ед. за стул. Позднее выяснилось, что в другом месте компьютеры можно приобрести по 19,5 тыс. усл. ед., а столы – по 8 тыс. усл. ед., а стулья по той же цене, благодаря чему на ту же сумму было куплено на 1 стол больше. Выяснить, какое количество единиц каждого вида оборудования было приобретено.

Решение: Пусть в соответствии с первоначальным планом компьютеров было , столов - , а стульев - . Поскольку по условию всего предметов должно было быть 29, получаем первое уравнение:

.

Далее, в соответствии с первоначальным планом, известно, что

.

С другой стороны, в соответствии со вторым планом,

.

Раскрывая в последнем условии скобки и перенося третье слагаемое в правую часть, получаем следующую систему:

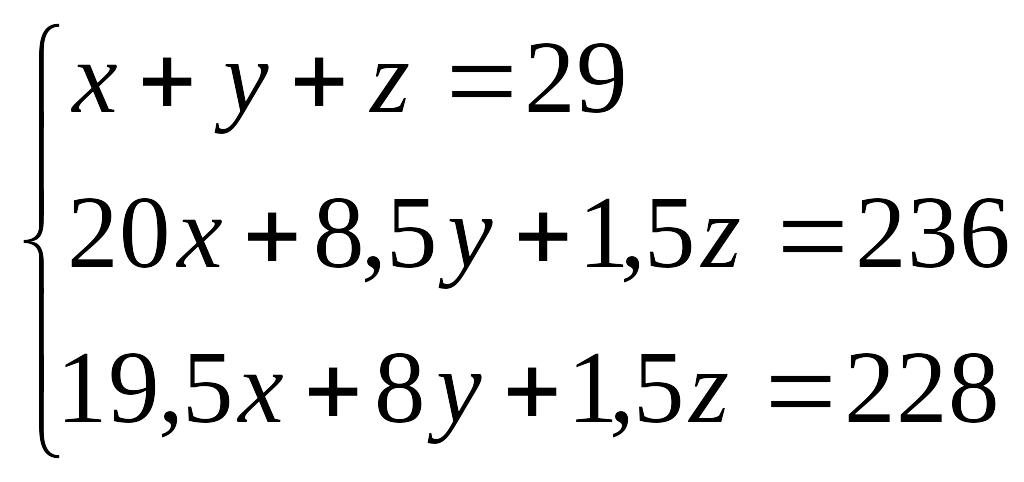
С помощью MathCadа было бы естественно решить данную систему методом обратной матрицы (см. § 1). Однако, как мы уже видели, данный метод “срабатывает” не всегда, поэтому здесь в качестве примера программирования в MathCade приводится и метод Гаусса тоже.

Метод обратной матрицы:

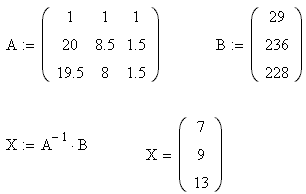
Таким образом, компьютеров было закуплено 7, столов – 10 (мы рассчитывали значения первоначального плана - 9, а в реальности было куплено на 1 больше), а стульев – 13.

Метод Гаусса:

Зададим в MathCade расширенную матрицу данной системы:

Далее введем счетчик числа элементов в каждой строке – он даст нам возможность выполнять необходимые действия сразу со всеми элементами. Для этого выполним следующие действия:

1) Ввести с клавиатуры j : =

2) Выбрать на панели ”Матрица” значок диапазона ”m..n” (во втором ряду второй слева) и вписать в него числа 0 и 3 (это означает, что мы будем работать с 0-м, 1-м, 2-м и 3-м элементами каждой строки).

Если все выполнено правильно, то на экране появится следующее выражение:

В данном случае, не совсем обычным для восприятия является нумерация строк и столбцов не с единицы, а с нуля - это используется MathCadом по умолчанию. При желании, в настройках пакета данное условие можно изменить.

Из второй строки вычтем первую, домноженную на 20, а из третьей – первую, домноженную на 19,5 – этим мы получим нули в первом столбце. В MathCade это будет выглядеть так:

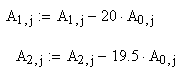
Тогда исходная матрица примет следующий вид (просто выведем ее на экран):

Из третьей строки вычтем вторую, а вторую строку разделим на (-11,5) и вновь выведем матрицу на экран:

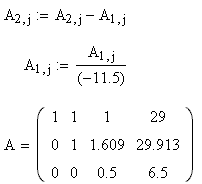
Разделим последнюю строку на 0,5 и этим действием закончим прямой ход Гаусса.

Получим нули в предпоследнем столбце выше главной диагонали: из второй строки вычтем третью, домноженную на 1.609, а из первой – просто третью, затем из первой - вторую и вновь выведем матрицу на экран:

Последний столбец является искомым решением системы.

В данном случае специально была задана точность до третьего знака после запятой, поэтому значения получились не достаточно точными. По умолчанию, в MathCade поддерживается точность до пятнадцатого знака после запятой.