1. 3. Подгруппы и их свойства. Критерий подгруппы. Примеры

Определение и критерий подгруппы

Определение 1. 3. 1. Непустое подмножество H группы А называется подгруппой группы А, если H само является группой относительно групповой операции в А.

Замечание. Содержащееся в определении подгруппы требование к подмножеству группы А, быть группой относительно групповой операции, определённой в А, нельзя заменить определением, по которому подгруппой группы А называлось бы всякое подмножество группы А, само являющееся группой. Так множество положительных рациональных чисел является группой относительно умножения и содержится, как подмножество, в аддитивной группе всех рациональных чисел, но не будет, конечно, подгруппой этой группы.

Если H - подгруппа группы А, то пишут Н < А

Теорема 1. 3. 1. Единица 1_H и обратный a_H^-1 к а Н в подгруппе Н группы А совпадают с единицей 1 и обратным а^-1 в самой группе А.

Доказательство. Действительно, 1_H = 1_H · 1 = 1_H · а · а^-1 = а · а^-1 = 1 и а_H^-1 = а_H^-1 · а · а^-1 = а^-1 где а - произвольный элемент из H.

При доказательстве того, что некоторое подмножество Н группы А является подгруппой, удобнее всего бывает пользоваться следующей теоремой:

Теорема 1. 3. 2. (Критерий подгруппы). Для того, чтобы непустое подмножество Н группы А являлось подгруппой группы А необходимо и достаточно, чтобы одновременно выполнялись 2 условия:

1. Н должно быть замкнуто относительно групповой операции в А:

( а, b Н ) а · b Н;

2. Н должно быть замкнуто относительно операции взятия обратного элемента: ( a Н) ( а^-1 Н).

Доказательство. Необходимость следует из определения группы. Достаточность. Из справедливости закона ассоциативности в группе А следует его справедливость для элементов из Н, а из того, что множество Н ¢ из свойств 1) и 2) следует принадлежность к Н единицы группы А.

Замечание. Если группа < А, ·> - конечная, то проверка свойства 2) является излишней. Для того чтобы показать, что Н является подгруппой данной группы достаточно построить таблицу Кэли и убедиться, что результаты операции принадлежат Н.

Примеры подгрупп

1. Множество Н = {2^к, где k Z} является подгруппой

мультипликативной группы <Q*, ·>так как Н , H Q* и выполняются два условия критерия подгруппы:

1) a · b = 2^k+t H;

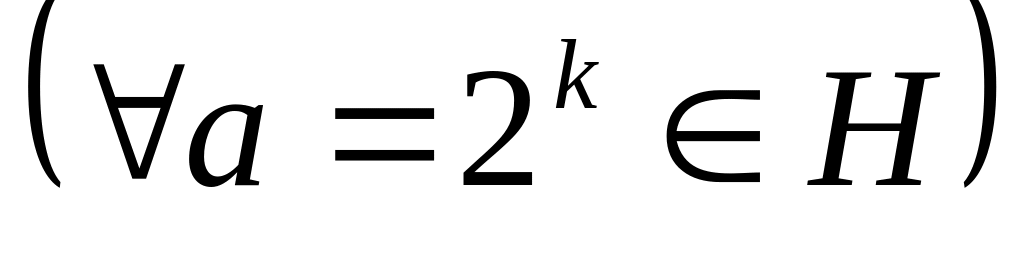
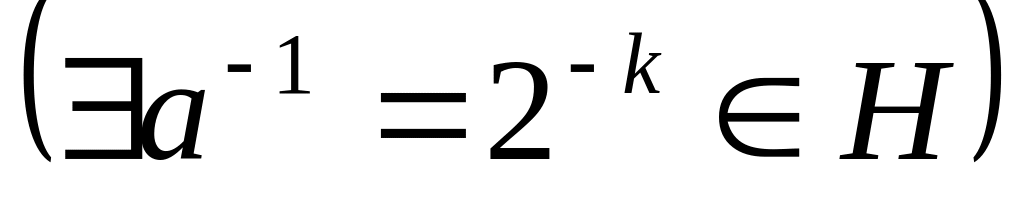2. (где k, t, k+ t, - k Z).

2. Несобственные подгруппы. Каждая группа имеет единичную подгруппу {1} и сама является своей подгруппой.

3. Циклические подгруппы. Зафиксируем элемент а в группе А. Подмножество (а) = {а^k | k Z} группы А, состоящее из всевозможных целых степеней элемента а, является подгруппой в А, называемой циклической подгруппой группы А, порождённой элементом а. Сам элемент а называется образующим (порождающим) циклической подгруппы (а).

Группа А, совпадающая с некоторой своей циклической подгруппой (а), называется циклической и состоит из элементов ... а^-2 , а^-1, а⁰ = 1, а¹ = а,... среди которых могут быть равные.

4. Подгруппы в аддитивной группе Z. Пусть Н - ненулевая подгруппа в Z и п - наименьшее положительное число из Н. Возьмём в Н произвольный элемент а разделим его с остатком на п, получим а= п · к + р (0 р< п). Т.к. а, п Н, то п · к Н, - п · к Н и р = а + (- пк) Н. В силу минимальности п, р = 0, т.е. а = пк п Z - множеству всех целых чисел, делящихся на п, которое, очевидно, является циклической подгруппой в Z, пZ = (n). Таким образом, Н = пZ. Итак, подгруппами в Z являются следующие циклические подгруппы: нулевая подгруппа (0) = {0} и бесконечные подгруппы пZ, порождённые различными натуральными числами п.

5. Некоторые подгруппы аддитивной группы С (комплексных чисел).

1) Множество всех чисел, изображаемых точками, лежащими на произвольной прямой, проходящей через начало координат.

2) Имеет место следующая цепочка: тZ < Z < Q < R < С.

3) {а + b · i | а, b А}, где А - любое из множеств п.2).

6. Некоторые подгруппы в мультипликативной группе С* всех ненулевых комплексных чисел.

1) Q* - множество всех ненулевых рациональных чисел;

2) R* - множество всех ненулевых действительных чисел;

3) R* · i - множество всех ненулевых чисто мнимых чисел;

4) C_n - множество всех комплексных корней n-ой степени из 1 (п N);

5. К - множество всевозможных комплексных корней из 1;

6. С¹ - множество комплексных чисел с единичным модулем.

7. Подгруппы группы симметрий правильного треугольника G :

{е}, {е, b}, {е, а · b}, {е, а² · b}, {е, а, a²}, G .

8. Подгруппы симметрической группы подстановок S₃:

{е}, {е }, {е },{е }, {е , }, S₃.

Замечание. Легко проверить, что пересечение любых двух подгрупп группы G является подгруппой группы G.