1. 2. Группы и их свойства. Примеры
Определение 1. 2. 1. Моноид < А, ∙> называется группой, если каждый элемент из А симметризуем.
Это наиболее распространённое и естественное современное определение группы. Выпишем данное определение группы более подробно:
Определение 1. 2. 2. Группой называется множество А с заданной на нем бинарной алгебраической операцией, удовлетворяющей следующим трём аксиомам (используем мультипликативную форму записи):
А1. ( а, b, с А) (а ∙ b) ∙ с = а ∙ (b ∙ с) (ассоциативность),
А2. ( 1 A)( а А) а ∙ 1 = 1 ∙ а = а (наличие единицы),
A3. ( а А) ( а' А) а ∙ а' = а'∙ а = 1 (обратимость элементов), где 1- единица из А; её существование обеспечивается аксиомой 2 и, как мы уже знаем, она единственна.
Замечание. Для доказательства того, что множество А с операцией * является группой, нужно:
1)
показать, что операция * является бинарной
операцией на множестве А,
т.е. выполнимой и однозначной операцией
ранга
2
(в
операции участвуют 2 элемента из А:
(а,
b)
а
*
b);
2) проверить выполнимость аксиом A1, А2, А3.
Если первое из этих условий не выполняется, то нет смысла в проверке аксиом.
Примеры групп:
1. Покажем, что < Z, + > - группа:
операция “+” является выполнимой на Z, так как ( а, b Z) а + b Z; однозначной на Z, так как результат (а + b) определяется однозначно; ранг операции равен 2, так как в операции используется два элемента (a, b) а+ b (следовательно, < Z, + > - группоид);
А1 выполняется, так как сложение целых чисел ассоциативно:
( а, b, с Z) (а+ b) + с = а + (b+ с), следовательно, < Z, + > - полугруппа;
А2 выполняется: роль нейтрального элемента будет играть число 0, так как ( а Z) а + 0 = 0 + а = а, следовательно, <Z, +> – моноид;
А3 выполняется: для всякого целого числа существует противоположное число ( а Z) ( – а Z) а + (– а) = (– а) + а = 0 , следовательно, < Z, + > – группа.
2. < А, + >, где А = п Z, или А = Q , или А = R, или А = С; п - неотрицательное целое число.
3. < А, >, где А = Q*, или А = R* или С*, или А= Q+, или А= R+;
Q*(Q+) - множество всех ненулевых (положительных) рациональных чисел, R* (R+) - множество всех ненулевых (положительных) действительных чисел, С* - множество всех ненулевых комплексных чисел.
4. < А, >, где А = {1}, или А = {1, – 1}, или А= {1, –1, i, – i}.
5. Множество всех матриц одинаковой размерности с действительными элементами относительно операции сложения матриц.
6. Множество всех невырожденных квадратных матриц одинакового порядка с действительными элементами относительно операции умножения матриц.
7. Множество всех биекций, т. е. взаимно однозначных отображений некоторого множества М на М с операцией композиции отображений.
8. Множество всех симметрии (самосовмещений) геометрической фигуры ни плоскости или в пространстве с операцией последовательного выполнения самосовмещений.
Рассмотрим
подробнее группу G
= {е,
а, а2,
b,
а
b,
а2
b}
симметрий правильного
треугольника,
где а
– поворот на 120°
вокруг центра правильного треугольника
против часовой стрелки, b
-
осевая симметрия относительно вертикальной
оси, проходящей через высоту треугольника
(Рис.
1).
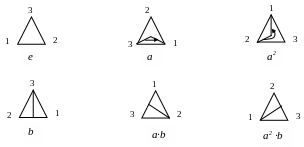
Рис. 1
Тогда а3 = b2 = е (е - тождественное самосовмещение треугольника).
b а = а b (где b а - композиция отображений; последовательно выполняется вначале отображение а, затем – b).
9. Множество С[х] всех многочленов от одного неизвестного с комплексными коэффициентами относительно операции сложения многочленов.
10. Множество всех непрерывных числовых функций относительно операции поточечного сложения функций.
11. Множество всех непрерывных, не обращающихся в нуль числовых функций относительно операции поточечного умножения функций.
12. Для
n
N
множество
Zn
=
{0,1, 2, ..., n
- 1} с операцией а
b
= с, где
с
- остаток отделения а
+ b
на
с.
Как показывают примеры, группы бывают как конечные, так и бесконечные.
Определение 1. 2. 3. Число элементов конечной группы А называется её порядком и обозначается | А |.
Все группы можно разделить также на коммутативные или абелевы (в честь норвежского математика Хенрика Абеля) и некоммутативные.
Определение 1. 2. 4. Группа < А, ∙ > называется абелевой (коммутативной), если ( а, b А) а b = b а.
Перечислим ряд важнейших исходных свойств групп, непосредственно вытекающих из аксиом.
Свойства групп
Для произвольной группы < А, > имеем:
(1) в А существует единственная единица 1.
(2) для каждого а А существует однозначно определенный обратный элемент а А.
(3) в А однозначно разрешимы уравнения а х = b и у а = b для любых двух элементов а и b из А, именно, х = а-1 b и y = b а-1 .
(4) справедливы законы сокращения: а b = а с влечёт b = с и а с = b с влечёт а = b для любых а, b, с из А.
(5) в А имеет место обобщённый закон ассоциативности, а в случае абелевой группы - обобщённый закон коммутативности.
(6) (а-1)-1 = а для всех а А.
(7) (а1 а 2 … а n)-1 = аn-1 … а1-1 для любого конечного числа п элементов а1, ... , аn группы А. В частности, (an) - 1 = (a - 1)n.
(8) в А можно определить степень а произвольного элемента а А с произвольным целым показателем k:
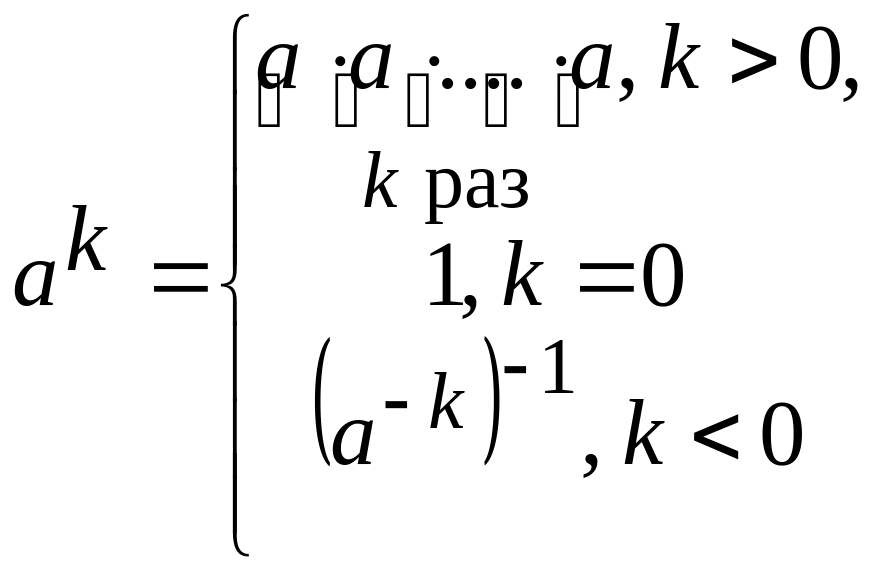
(9) в группе А можно определить операции деления: правое (а / b = а b-1) и левое (а \ b = b-1 а), при этом элементы а b-1 и b-1 а называют правым и левым частным элементов а и b соответственно.
Замечание. Для абелевой группы А обе операции деления совпадают.