Глава I. Теоретические основы развития умений и навыков решения логарифмических уравнений в процессе реализации учебных проектов

1.1. Логарифмические уравнения в школьном курсе математики

Рассмотрим историю возникновения логарифмов, она очень интересна своей разнообразностью применения. После открытия морского пути в Индию была переделана вся система мер на десятичную основу, возникли десятичные дроби, стали применять индийско-арабскую систему счисления. Другим большим усовершенствованием вычислительной техники было изобретение логарифмов. Логарифмы были введены в начале 17 века двумя математиками - Непером и Бюрги. Логарифмы были придуманы для ускорения и упрощения вычисления.

Впервые логарифмами воспользовался немецкий ученый Иоганн Кеплер (1571-1630) при составлении астрономических таблиц. Логарифмами он пользовался при обработке «Рудольфовых таблиц», основанных на наблюдениях выдающегося датского астронома Тихо Браге. Первая идея о логарифмическом вычислении возникла из сопоставления членов геометрической прогрессии с членами арифметической. Такое сопоставление ярко выражено у Архимеда. Дальнейшее развитие теории логарифмов связано с более широким применением аналитической геометрии исчисления бесконечно малых. К этому периоду относится установление связи между квадратурой равносторонней гиперболы и натуральным логарифмом [8].

Теория логарифмов этого периода связана с именами ряда математиков таких как: Сент – Винцент (в 1647 году нашел замечательное свойство равносторонней гиперболы, позволившее связать площадь, заключенную между кривой и её асимптотами, с натуральными логарифмами), Николаус Меркатор ( в 1677 году разработал новый более удобный способ вычисления логарифмов используя метод кадрирования площадей, ограниченных кривой вида y=xⁿ, абсциссой и двумя ординатами), Исаак Ньютон ( ввёл обобщенную теорему Бинома и метод обращения рядов), Брук Тейлор ( ввел новый метод вычисления логарифмов, основанный на непрерывных дробях), Леонард Эйлер (впервые изложил учение о логарифмах, исходя из определения логарифма как результат одного из двух действий, обратных действию возведения в степень).

Не меньшее значение имело изобретение логарифмов для развития теоретических вопросов математики. Возникнув из практических нужд вычислителей, астрономов и мореплавателей, идей логарифма привела в 18–19 веках к развитию учения о показательной и логарифмических функциях и других математических теорий, которые в свою очередь открыли возможность для новых практических применений [8].

И в те же далекие времена, ученые впервые стали задумываться и о равенствах содержащих неизвестные величины. Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: "Смотри!", "Делай так!", "Ты правильно нашел". В этом смысле исключением является "Арифметика" греческого математика Диофанта Александрийского (III в.) - собрание задач на составление уравнений с систематическим изложением их решений [50].

Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. Слово "аль-джебр" из арабского названия этого трактата - "Китаб аль-джебер валь-мукабала" ("Книга о восстановлении и противопоставлении") - со временем превратилось в хорошо знакомое всем слово "алгебра", а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.

Одним из видов таких уравнений явились логарифмические уравнения и в настоящее время изучение логарифмических уравнений предусмотрено государственным образовательным стандартом в общеобразовательных школах в 11 классе.

Проведем анализ наиболее используемых учебно-методических комплексов по алгебре 11 класса в школах республики Бурятии: А.Г. Мордкович «Алгебра и начала анализа» 10-11 класс, А. Н. Колмогоров «Алгебра и начала анализа» 10-11 класс, Н.Я. Виленкин «Алгебра и начала анализа» 11 класс (Приложение 1).

Рассмотрим содержание учебно-методического комплекса А.Г. Мордкович «Алгебра и начала анализа» 10-11 класс. Данный учебно-методический комплекс состоит из двух частей: учебника и задачника. В первой части данного учебно-методического комплекса материал, касающийся логарифмических уравнений, изучается в VII главе «Показательная и логарифмическая функция». Здесь логарифмические уравнения рассматриваются с самых общих позиций. Это, с одной стороны, своеобразное подведение итогов и, с другой стороны, некоторое расширение и углубление знаний. На изучения темы «Логарифмические уравнения и их решения» выделено 3 часа по программе 3 часа в неделю. В одном из параграфов этой главы подведены частичные итоги изучения в логарифмических уравнений. Использованы следующие термины: логарифмические уравнения, потенцирование, метод логарифмирования.

Сформулирована теорема о равносильности уравнений. Выделены три общих метода решения логарифмических уравнений:

1. Функционально-графический метод. Он основан на использовании графических иллюстраций или каких-либо свойств функций.

2. Метод потенцирования. Он основан на теореме, полученной в параграфе.

3. Метод введение новой переменной [29].

Система задач во второй части данного учебно-методического комплекса изложена в той же последовательности, что и соответствующий материал в первой части. В параграфе в данном учебно-методическом комплексе «Логарифмические уравнения» изложены различные типы заданий на решение логарифмических уравнений [28].

Учебно-методический комплекс А. Н. Колмогоров «Алгебра и начала анализа» 10-11 класс. Данный комплекс А.Н. Колмогорова отличается от учебно-методического комплекса А.Г. Мордковича. Учебный методический комплекс состоит из одной книги, которая включает в себя теорию и практику. Материал, касающийся логарифмических уравнений, изучается в данной главе в десятом параграфе «Показательная и логарифмическая функция». И в этом учебно-методическом комплексе Колмогоров объединил две темы в один пункт «Решение логарифмических уравнений и неравенств» Здесь логарифмические уравнения рассматриваются с самых общих позиций. На изучения темы «Логарифмические уравнения и неравенства, их решение» выделено 5 часов по программе 3 часа в неделю. В данном параграфе этой главы подведены частичные итоги изучения логарифмических уравнений и повторяется теорема о корне [40].

Выделены четыре общих метода решения логарифмических уравнений:

1. метод использование определение логарифмов.

2. метод использование теоремы о корне.

3. Метод введение новой переменной.

4. Метод логарифмирование.

После теории сразу идут упражнения для закрепления, в которых сочетаются различные типы заданий на решение логарифмических уравнений [17].

Учебно-методический комплекс Н.Я. Виленкин «Алгебра и начала анализа» 11 класс. Учебно-методический комплекс Н.Я. Виленкина, состоит из одной книги, куда входит и теория и практика по темам только 11 класса. Материал по теме «Логарифмические уравнения» входит в восьмую главу: «Показательная, логарифмическая и степенная функции», а именно во втором параграфе «Показательные и логарифмические уравнения н неравенства» [4].

В учебно-методическом комплексе Н.Я. Виленкина на изучение данной темы отводится 6 часов. Она разбита на два раздела и рассматривается одновременно с логарифмическими неравенствами. Первый раздел называется «Простейшие логарифмические уравнения и неравенства», в нем вводится понятие логарифмического уравнения, корня логарифмического уравнения и рассматриваются простейшие примеры. Второй раздел называется «Решение логарифмических уравнений и неравенств», в нем формулируются теорема о равносильности системы, состоящей из уравнения и неравенства. Также в данном пункте дается алгоритм решения логарифмических уравнений, и далее рассматриваются более сложные примеры решения логарифмических уравнений.

В данном учебном пособии выделяются четыре метода решения логарифмических уравнений:

1. метод использование определение логарифмов.

2. метод использование теоремы о равносильности системы.

3. Метод введения новой переменной

4. Метод логарифмирования [4].

Из всех рассмотренных учебно-методических комплексов составим тематическое планирование по учебному методическому комплексу А.Г. Мордкович «Алгебра и начала анализа» 10-11 класс по теме «Логарифмические уравнения», на которое мы будем опираться в нашем исследовании. Данное тематическое планирование состоит из столбцов: номер урока, цели урока, заданий и упражнений в классе и дома, видов самостоятельной работы, средств обучения, тем повторения [28].

Таблица№1

Тематическое планирование по учебному методическому комплексу А.Г. Мордкович «Алгебра и начала анализа» 10-11 класс по теме «Логарифмические уравнения»

Тема урока	Цели урока	Распределение заданий и упражнений			Самостоятельная работа	Средства обучения	повторения
		В классе		дома
Лога рифми- ческие уравне- ния	формировать умение решать логарифмические уравнения; ввести понятие операции потенцирования; формировать умение применения трех основных методов решения логарифмических уравнений.	№1550 1552, 1554, 1558	№ 1549, 1551, 1555, 1559; теория в учебнике стр. 304-306.		Карточки с самостояте- льной работой	Карточки с самостояте- льной работой, цветной мел.	Лога- рифми- ческая функциясвойство логариф-мов.
Лога- рифми- ческие уравне- ния	развить умение решать логарифмические уравнения; закрепить умение применения трех основных методов решения уравнений; отработать навыки решения логарифмических уравнений, используя свойства.	№1563, 1564, 1565 №1572.		№1561, 1566-1571(а); теория в учебни- ке стр. 306-308.	Провероч- ная работа	Карточки с провероч- ной работой	Логари- фмичес- кие уравне- ния, 3 основ- ных метода.
Лога- рифми- ческие уравне- ния	закрепить умение решения логарифмических уравнений; отработать умение применения трех основных методов решения уравнений; закрепить навыки решения логарифмических уравнений, используя свойства логарифмов.	С/работа		С/рабо- та	С/работа	Карточки с провероч- ной работой	Лога- рифми- ческая функция, св-во лога-рифмов. Логар-ие уравне- ния

Логарифмическая функция традиционно является одной из важнейших составных частей школьного курса математики. И этот курс предполагает образовательные задачи, решить которые, как правило, можно, пройдя целенаправленную специальную подготовку [18].

Таким образом, в наиболее часто применяемых в обучении школьных учебных методических комплексах по математике в полной степени определяет место логарифмических уравнений в линии изучения уравнений.

Далее рассмотрим линию изучения логарифмических уравнений. Теме «Решение логарифмических уравнений» часто предшествует изучение таких тем как «Преобразование логарифмических выражений», «Логарифмическая функция и ее график», «Свойства логарифмической функций».

Опыт преподавания математики показывает, что осознание важности изучаемого материала приходит к ученикам не в процессе его изучения, а в процессе его применения при решении других заданий, т.е. тогда, когда процесс осознания становится средством для решения других задач.

Так, например, решение уравнения , сводится к простейшему уравнению , причём к частному виду простейшего, после элементарного преобразования выражения, стоящего в левой части уравнения с помощью введения новой переменной и применения формул логарифмической функции [21].

Мы видим, что именно здесь учащиеся могут наблюдать пользу от изучения формул логарифмической функции. С их помощью нерешаемое на первый взгляд уравнение принимает достаточно простой и, главное, знакомый вид.

При таком подходе изучения логарифмической функции, когда уравнения изучаются после формул преобразования логарифмических выражений, место логарифмических уравнений определяется через систематизацию знаний по темам «Преобразование логарифмических выражений» и «Основные свойства логарифмической функции и ее график».

Роль изучения логарифмических уравнений неизмеримо велика. Ну и как следствие из этого велико и неизмеримо место изучения методов решения и логарифмических уравнений. Т.к. авторы учебно-методических комплексов не уделяют должного внимания обозначению методов решения логарифмических уравнений, попробуем классифицировать методы решения логарифмических уравнений [18].

В настоящее время наиболее часто для решения логарифмических уравнений используют восемь основных методов: потенцирование, использование определения логарифма, приведение к квадратному уравнению, логарифмирование, приведение к одному основанию, введение вспомогательной переменной, графический и метод подбора. Рассмотрим теперь поподробнее каждый метод решения логарифмических уравнений.

Но перед этим вспомним две теоремы, которые помогут нам решить логарифмические уравнения [41].

Теорема 1. Уравнение (1) равносильно системе

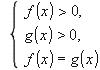(2)

Для решения уравнения (1) достаточно решить уравнение (3)

и его решения подставить в систему неравенств

(4), задающую область определения уравнения (1).

Корнями уравнения (1) будут только те решения уравнения (3), которые удовлетворяют системе (4), т.е. принадлежат области определения уравнения (1).

При решении логарифмических уравнений может произойти расширение области определения (приобретение посторонних корней) или сужение (потеря корней). Поэтому подстановка корней уравнения (3) в систему (4), т.е. проверка решения обязательна [41].

Рассмотрим уравнение вида:

log_a(x)f(x)= log_a(x)g(x) (5).

Теорема 2: Уравнение (5) равносильно системе

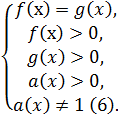
Корнями уравнения (5) будут только те корни уравнения , которые принадлежат области определения, задаваемой условиями ≠1, уравнения (3) в систему (4), т.е. проверка решения, обязательна.

Первый и самый распространенный метод-это метод потенцирования т.е. применение свойств логарифма [38].

1. Потенцинирование (применение свойств логарифма).

Пример 1: Решить уравнение

Решение: В силу теоремы 2 данное уравнение равносильно системе:

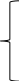Х²-1=5-х,

Х²-1>0,

5-х>0,

Х+4>0,

Х+4≠1.

Решим уравнение:

х₁=2, х₂=-3.

Всем условиям системы удовлетворяет лишь один корень. Ответ:

2. Использование определения логарифма [21].

Пример 2: Найти х, если

Решение:

х-1≠1

Значение х = 3 принадлежит области определения уравнения. Ответ х = 3

3. Приведение к квадратному уравнению [40].

Пример 3: Решить уравнение

lg x=3

lg x=-4/3

x=10^-4/3

и lgx≠0.

Оба значения х являются корнями уравнения [46].

Ответ:

4. Логарифмирование.

Пример 4: Решить уравнение

Решение: Прологарифмируем обе части уравнения по основанию 10 и применим свойство "логарифм степени".

Оба корня принадлежат области допустимых значений логарифмической функции.

Ответ: х = 0,1; х = 100

5. Приведение к одному основанию.

Пример 5: Решить уравнение

Воспользуемся формулой и перейдем в каждом из слагаемых к логарифму по основанию 2:

Тогда данное уравнение примет вид:

Так как , то это корень уравнения [21].

Ответ: х = 16

6. Введение вспомогательной переменной.

Решим способом введения вспомогательной переменной уравнение, заданное в примере 5.

Решить уравнение:

Пусть ; тогда

Учитывая, что

Получим уравнение:

После проверки, проведенной устно, легко убеждаемся в правильности найденного ответа.

Ответ: х = 16

7. Графический способ.

Многие уравнения, содержащие переменную не только под знаком логарифма или в показателе степени, удобно решать графически.

Графически решением уравнения являются абсциссы точек пересечения графиков функций, заданных в уравнении [40].

Пример 7: Решить уравнение

Решение: Построим графики функций и y = x

Рис. 1

Графики функций не пересекаются, и, значит, уравнение не имеет корней (рис. 1). Ответ: корней нет

8. Метод подбора.

Пример 8: Найти х, если

Решение: С помощью рассмотренных выше способов корни уравнения найти не удается. Найдем какой-нибудь корень методом подбора.

Пусть, например, х = 10. Проверкой убедимся в том, что 10 - корень уравнения. Действительно,

истинно

Докажем, что других корней данное уравнение не имеет.

Эти корни следует искать во множестве значений х.

Допустимые значения х находятся в промежутке . На этом промежутке функция убывает, а функция возрастает. И, значит, если уравнение имеет решение, то оно единственное [40].

Ответ: х = 10.