Умовний екстремум функції багатьох змінних

Нехай в області D задано функцію z = f (x, у) і лінію L, яка визначається рівнянням (х, у) = 0 та лежить в цій області.

Задача полягає в тому, щоб на лінії L знайти таку точку М (х; у), в якій значення функції f (х, у) є найбільшим або найменшим порівняно із значеннями цієї функції в інших точках лінії L. Такі точки М називають точками умовного екстремуму функції f (x, у) на лінії L. На відміну від звичайного екстремуму значення функ­ції в точці умовного екстремуму порівнюється із значеннями цієї функції не в усіх точках області D (чи - околу точки М), а лише в точках, які лежать на лінії L.

Назва «умовний екстремум» пов'язана з тим, що змінні х та у мають додаткову умову: (х, у) = 0.

Рівняння (х, у) = 0 називається рівнянням зв'язку; якщо це рівняння можна розв'язати відносно однієї змінної, наприклад у: у = (х), то підставляючи замість у значення (х) у функцію z = f (х, у), дістаємо функцію однієї змінної z = f (х, (х)). Оскіль­ки додаткова умова врахована, то задача знаходження умовного екс­тремуму зводиться до задачі на звичайний екстремум функції однієї змінної.

Проте не завжди можна розв'язати рівняння зв'язку відносно у чи х. Тоді розв'язують поставлену задачу так.

Розглянемо функцію z = f (х, у), де у= (х), як складену функ­цію. З необхідної умови екстремуму випливає, що в точках екстремуму

(1)

У цьому випадку означає похідну неявної функції, заданої рівнянням зв'язку (х, у) = 0:

, тому 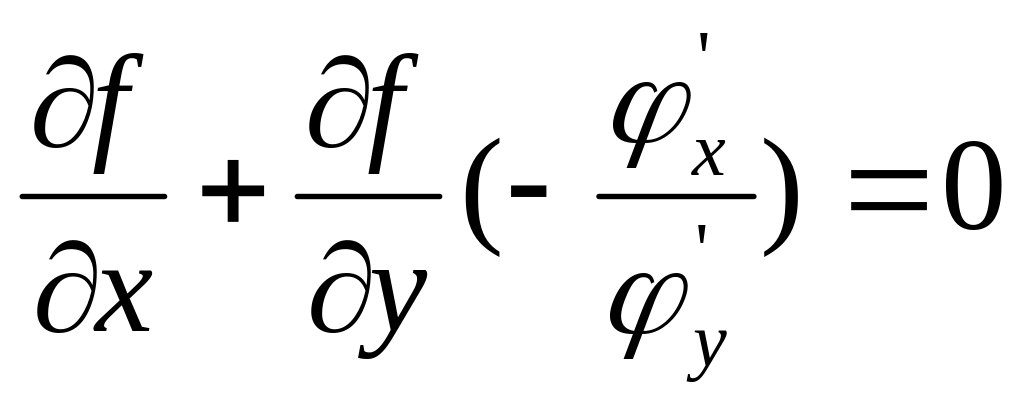, тобто

Позначивши останні відношення через (- λ) (λ≠ 0) (знак мінус взято для зручності, а саме число λ може мати довільний знак), знайдемо, що в точці умовного екстремуму виконуються умови

, тобто

Отже, стаціонарні точки умовного екстремуму мають задовольняти систему рівнянь:

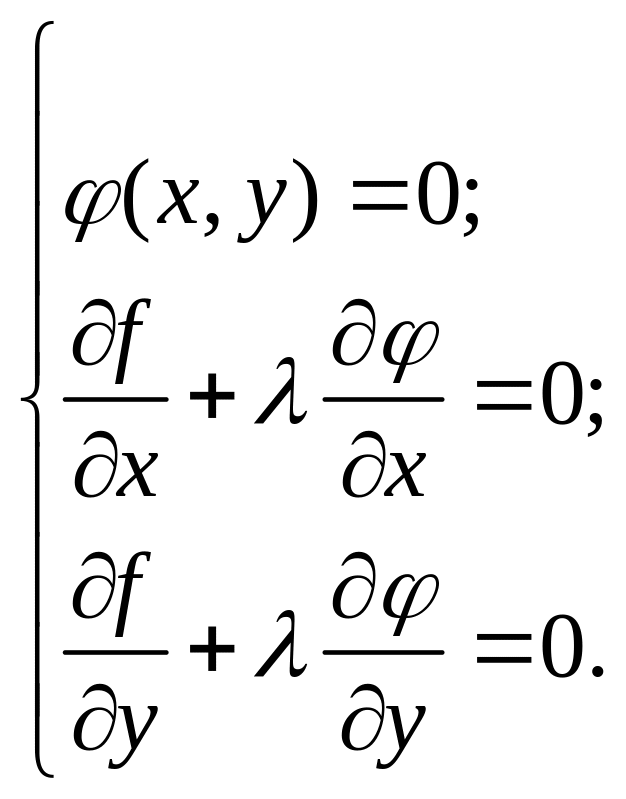
Аналізуючи цю систему, помічаємо, що знаходження умовного екстремуму функції z = f (х, у) звелось до знаходження звичайного екстремуму функції

Функція (3) називається функцією Лагранжа, а число – множ­ником Лагранжа.

Умови (2) є лише необхідними. Вони дають змогу знайти стаціо­нарні точки умовного екстремуму. З теореми 2 випливає, що характер умовного екстремуму (достатні умови) можна встановити за знаком диференціала другого порядку функції Лагранжа: якщо в стаціонарній точці >0

( < 0), то ця точка є точкою умов­ного мінімуму (максимуму).

Для функції U= f (х, у, z) з рівняннями зв'язку (х, у, z) = 0, (х, у, z) = 0 функція Лагранжа записується у вигляді

Стаціонарні точки умовного екстремуму знаходяться із системи рівнянь

а достатні умови існування умовного екстремуму в цих точках можна визначити за знаком диференціала .

Розглянутий метод можна поширити на дослідження умовного екстремуму функції довільного числа змінних.

Правило знаходження точок умовного екстремуму функції z = f (х, у):

1. Складаємо функцію Лагранжа:

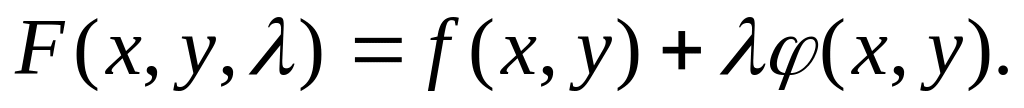
2. Знаходимо стаціонарні точки із системи рівнянь:

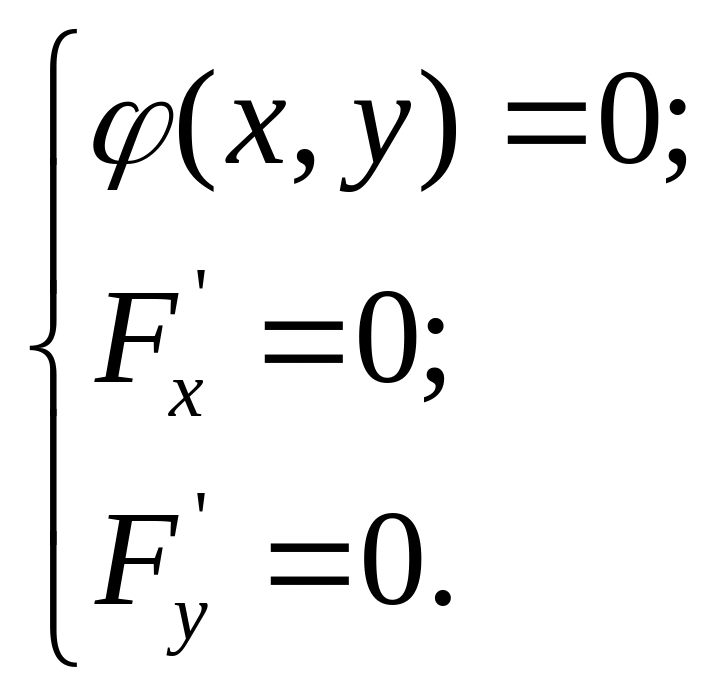
3. Якщо в стаціонарній точці >0 ( < 0), то в цій точці функція має умовний мінімум (максимум).

Приклад:

Знайти найбільше і найменше значення функції z=xy, якщо x та у додатні і задовольняють рівняння зв’язку

Складемо функцію Лагранжа (3):

(

Користуючись системою (2), знаходимо стаціонарні точки цієї функції:

звідки х=2, у=1, =-2.

Отже, маємо одну стаціонарну точку М(2; 1; -2 ). Щоб визначити характер умовного екстремуму в цій точці, знайдемо за допомогою формули

другий диференціал функції Лагранжа при =-2:

Знайшовши з рівняння звязку dy(2;1)= , дістанемо

<0,

тому точка (2; 1) є точкою умовного максимуму функції z=xy. При цьому z =2.

Цей результат легко перевірити, знайшовши звичайний екстремум функції:

Приклад:

Знайти умовний екстремум функції z=x+y якщо х та у задовольняють рівняння зв'язку

Складемо функцію Лагранжа:

Користуючись системою (2), знаходимо стаціонарні точки цієї функції:

Із другого рівняння маємо , із третього . Підставляючи ці значення в перше рівняння, дістанемо Звідки

Отже, маємо дві стаеціонарні точки: М (- ; - ), М ( ; ). Далі необхідно зясувати, чи є знайдені точки точками екстремуму. Для цього обчислюємо значення другого диференціала функції у цих точках, вважаючи параметром. Знаходимо частинні похідні другого порядку

та диференціал другого порядку

при маємо >0, то в т. М (- ; - ) маємо умовний мінімум: z (- ; - ) = - - = - .

При <0, то в т. М ( ; ) маємо умовний максимум: z ( ; ) = + = .

Відповідь: z = - ,

z = .

Приклад:

Знайти умовний екстремум функції z=xy, якщо х та у задовольняють рівняння звчязку 4х-3у=12.

знаходимо стаціонарні точки:

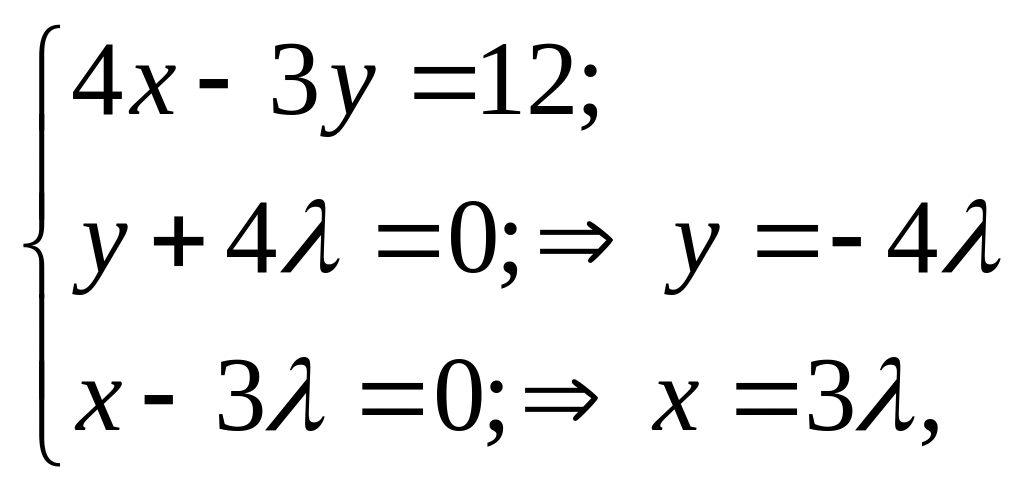
тоді 12 +12 =12; 24 =12; =

х=1,5; у=-2; z=-3.

Точка (1,5; -2; -3) – стаціонарна точка.

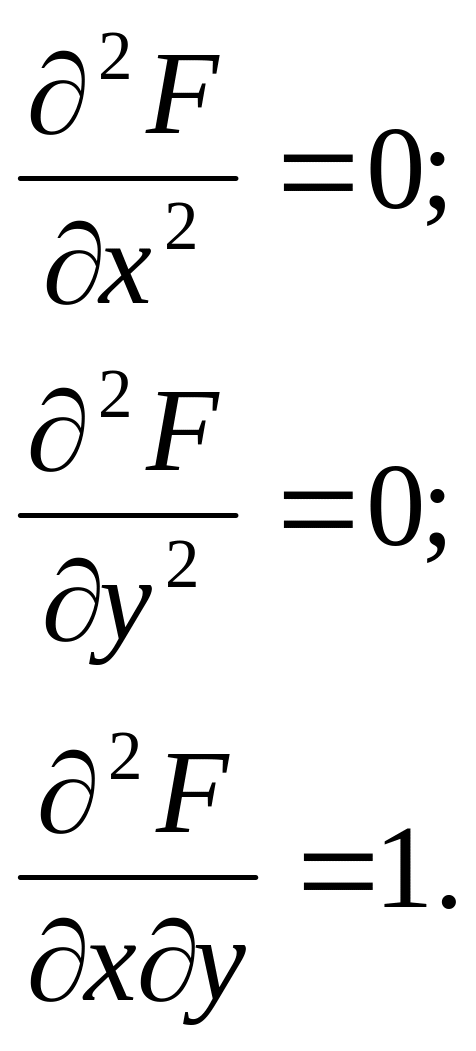
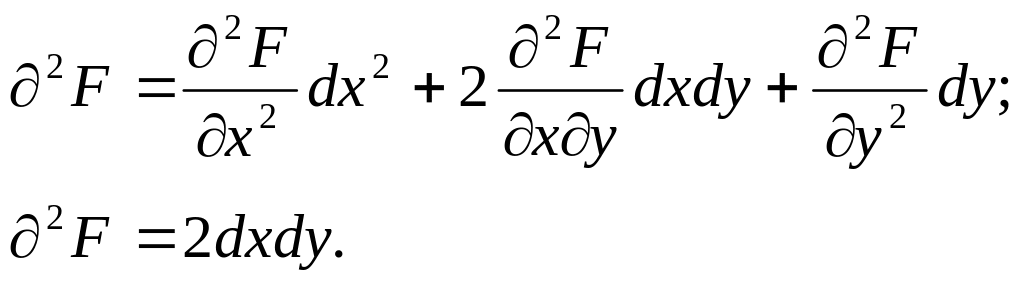
Знайдемо із рівняння звязку: , тоді

>0, тоді т.(1,5; -2; -3) є точкою умовного мінімуму функції z=xy.

z = -3.

ІІ спосіб

З рівняння звязку , тоді функція z=x·y при підстановці у буде функцією однієї змінної:

Знаходимо критичні точки першого роду:

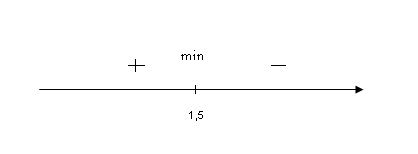
z (1,5) = -3.

Можна визначити характер умовного екстремуму в точці 1,5 за допомогою частинної похідної другого порядку по змінній х: >0 х = 1,5 функція z=xy має умовний мінімум.