
- •Общая постановка задачи оптимизации.
- •Классическая задача на условный экстремум. Необходимые и достаточные условия условного экстремума.
- •Метод множителей Лагранжа для решения классической задачи на условный экстремум.
- •Линейные неравенства и область решений системы линейных неравенств.
- •5. Общая задача линейного программирования. Геометрическая интерпретация задачи.
- •Графический метод решения задачи линейного программирования для двух переменных.
- •Решение задачи линейного программирования симплекс–методом. Симплексные таблицы. Алгоритм симплекс–метода.
- •Решение задачи оптимизации выпуска продукции симплекс–методом.
- •Модель оптимизации плана перевозок (транспортная задача). Экономическая постановка задачи.
- •9.2 Основные свойство транспортной задачи
- •9.3 Двойственная задача
- •9.4 Теоремы двойственности
- •9.5 Построение опорного плана транспортной задачи
- •9.6 Метод севево-западного угла
- •Математическая модель транспортной задачи. Открытые и закрытые задачи. Допустимый, опорный и оптимальный планы перевозок.
- •11. Построение начального (опорного) плана перевозок по методу северо–западного угла и по методу наименьшей стоимости.
- •12. Теорема о потенциалах. Метод потенциалов. Транспортные таблицы. Понятие цикла. Сущность метода потенциалов.
- •13.Критерий оптимальности и неоптимальности опорного плана. Критерий единственности оптимального опорного плана.
- •14. Понятия испытания и случайного события. Частота и относительная частота появления события в серии испытаний. Вероятность случайного события.
- •15. Совместные и несовместные события. Полная группа событий. Событие, благоприятствующее данному. Равновозможные события. Совокупность элементарных исходов.
- •16.Классическое определение вероятности. Простейшие свойства вероятности.
- •17. Основные правила комбинаторики. Сочетания, перестановки, размещения.
- •18. Частота и относительная частота появления события в серии испытаний. Стохастическая устойчивость случайного события. Статистическое определение вероятности.
- •19. Вероятность противоположного события. Условная вероятность.
- •20. Сумма и произведение случайных событий. Теорема сложения вероятностей: для двух произвольных событий, для двух несовместных.
- •21. Теорема умножения вероятностей: для двух произвольных событий; для двух независимых событий; для нескольких событий, независимых в совокупности.
- •22. Формула полной вероятности.
- •23. Теорема Байеса.
- •24. Формула Бернулли
- •25. Локальная и интегральная теоремы Лапласа. Функции Гаусса и Лапласа.
- •26. Понятие случайной величины. Закон распределения случайной величины. Функция распределения и ее свойства.
- •1) Биномиальное распределение (дискретное)
- •2) Пуассоновское распределение (дискретное)
- •3) Показательное распределение (непрерывное)
- •4) Равномерное распределение (непрерывное)
- •5) Нормальное распределение или распределение Гаусса (непрерывное)
- •27. Дискретная случайная величина. Способы задания закона распределения дискретной случайной величины.
- •28. Числовые характеристики дискретной случайной величины: математическое ожидание, дисперсия, среднее квадратическое отклонение. Их основные свойства.
- •29. Биномиальный закон распределения.
- •30. Распределение Пуассона. Простейший поток событий.
- •Ц.П.Т. Ляпунова
- •Слабый закон больших чисел
- •Усиленный закон больших чисел
- •Значение теоремы Чебышева для практики.
- •51. Понятие критерия. Критическая область и область принятия гипотезы. Односторонняя и двусторонняя критическая область, критические точки. Мощность критерия.
- •56. Коэффициенты регрессии. Линии регрессии.
- •59. Эмпирическая и теоретическая линии регрессии.
27. Дискретная случайная величина. Способы задания закона распределения дискретной случайной величины.
Говорят,
что задана дискретная
случайная величина ![]() ,
если указано конечное или счетное
множество чисел
,
если указано конечное или счетное
множество чисел
![]()
и
каждому из этих чисел ![]() поставлено
в соответствие некоторое положительное
число
поставлено
в соответствие некоторое положительное
число ![]() ,
причем
,
причем
![]()
Числа ![]() называются
возможными значениями
случайной величины
,
а числа
называются
возможными значениями
случайной величины
,
а числа![]() - вероятностями этих
значений (
- вероятностями этих
значений ( ![]() ).
).
Таблица
![]()
называется законом распределения дискретной случайной величины .
Для
наглядности закон
распределения дискретной случайной
величины изображают
графически, для чего в прямоугольной
системе координат строят
точки ![]() и
соединяют последовательно отрезками
прямых. Получающаяся при этом ломаная
линия называется многоугольником
распределения случайной величины
.
и
соединяют последовательно отрезками
прямых. Получающаяся при этом ломаная
линия называется многоугольником
распределения случайной величины
.
Если возможными значениями дискретной случайной величины являются 0, 1, 2, …, n, а соответствующие им вероятности вычисляются по формуле Бернулли:
![]()
то говорят, что случайная величина имеет биномиальный закон распределения:
![]()
Пусть
заданы натуральные
числа m, n, s, причем ![]() Если
возможными значениями дискретной
случайной величины
являются 0,1,2,…,
m,
а соответствующие им вероятности выражаются
по формуле
Если
возможными значениями дискретной
случайной величины
являются 0,1,2,…,
m,
а соответствующие им вероятности выражаются
по формуле
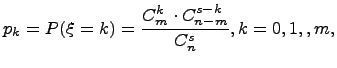
то говорят, что случайная величина имеет гипергеометрический закон распределения.
Другими часто встречающимися примерами законов распределения дискретной случайной величины являются:
геометрический
![]()
где ![]() ;
;
Закон распределения Пуассона:
![]()
где
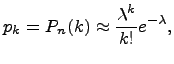
![]() -
положительное постоянное.
-
положительное постоянное.
Закон
распределения Пуассона является
предельным для биномиального при ![]() ,
,![]() ,
, ![]() .
Виду этого обстоятельства при больших n и
малых p биномиальные вероятности
вычисляются приближенно по формуле
Пуассона:
.
Виду этого обстоятельства при больших n и
малых p биномиальные вероятности
вычисляются приближенно по формуле
Пуассона:
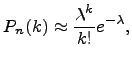
где ![]() .
.
28. Числовые характеристики дискретной случайной величины: математическое ожидание, дисперсия, среднее квадратическое отклонение. Их основные свойства.
Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл.
Свойства математического ожидания:
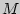 [
[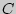 ]
=
,
где
- const;
]
=
,
где
- const;[
 ]
=
]
=  [
[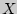 ];
];[X
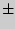 Y]
=
[
]
Y]
=
[
] 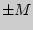 [
[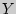 ];
];[X
 Y]
=
[
]
Y]
=
[
] 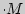 [
],
где
и
-
независимые
[
],
где
и
-
независимые
Дисперсия - среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической. В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий:
1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:
![]()
2. Взвешенная дисперсия (для вариационного ряда):
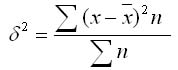
где n - частота (повторяемость фактора Х)
Среднее квадратичное отклонение определяется как обобщающая характеристика размеров вариации признака в совокупности. Оно равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической, т.е. корень из дисперсии и может быть найдена так:
1. Для первичного ряда:
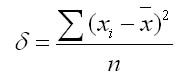
2. Для вариационного ряда:
![]()
Преобразование формулы среднего квадратичного отклонени приводит ее к виду, более удобному для практических расчетов:
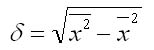
Среднее квадратичное отклонение определяет на сколько в среднем отклоняются конкретные варианты от их среднего значения, и к тому же является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, и поэтому хорошо интерпретируется.
