17(1). Ряды Фурье.

Пусть на [a;b] задана функция f(x). Разобьем [a;b] на части точками деления , совокупность которых – Т – назовём разбиением отрезка [a;b]. Пусть - длина k-го отрезка разбиения, . На каждом , , выберем произвольным образом точку . Обозначим выбор точек через .

Величина называется интегральной суммой Римана функции f на отрезке [a;b], соответствующей разбиению Т и выбору .

Опр. Если существует предел I интегральных сумм при , не зависящий от способа деления отрезка [a;b] на части и выбора точек , то функция f называется интегрируемой по Риману на отрезке [a;b], а сам этот предел –определённым интегралом Римана функции f: .

Опр.1. Система интегрируемых на функций называется ортогональной на , если

Примером ортогональной на системы функций является три­гонометрическая система

Опр.2. Тригонометрическим рядом называется функцио­нальный ряд вида

. (1)

Если тригонометрический ряд (1) сходится равномерно на числовой оси к функции ,то его коэффициенты вычисляются по формулам

Опр.3. Для -периодической интегрируемой на оси функ­ции введенные выше числа и называются коэффициентами Фурье функции . Ряд Фурье функции имеет вид

Таким образом, равномерно сходящийся на оси тригонометрический ряд является рядом Фурье своей суммы.

Опр.4. Посл-ть наз-ся равно­мерно сходящейся к ф-ии f(х) на мн-ве Е, если .

Опр.5. Для интегрируемых на функций и , число 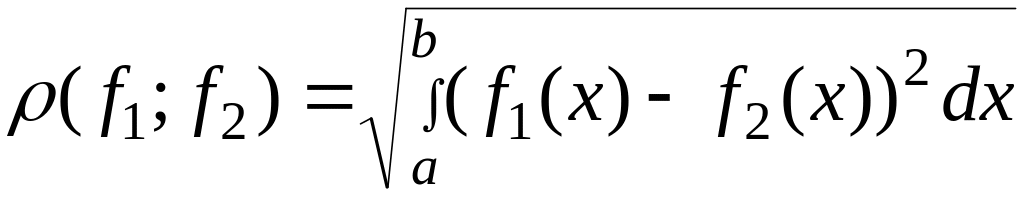называется расстоянием в среднем квадратичном между этими функциями.

Опр.6.Для функций , , n=1,2,…, интегри­руемых на , последовательность {f_n(x)} называется сходящейся в среднем квадратичном к функции f(x), если .

Следует отметить, из равномерной сходимости следует сходимость в среднем квад­ратичном, но не наоборот.

Т.1. Минимальное свойство частичных сумм ряда Фурье. Среди всех тригонометрических многочленов

порядка не выше n наименее уклоняется в среднем от функции f(x) n-я частичная сумма ее ряда Фурье

.

Рассмотрим

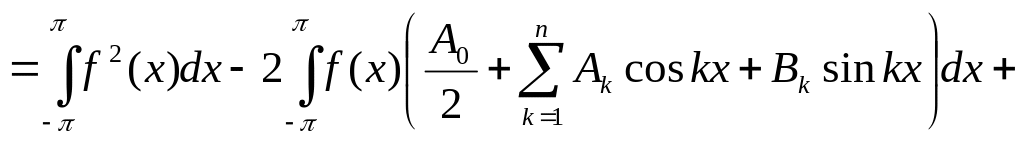
Ортогональность тригонометрической системы занулит все слагаемые, кроме содержащих квадраты ф-ций

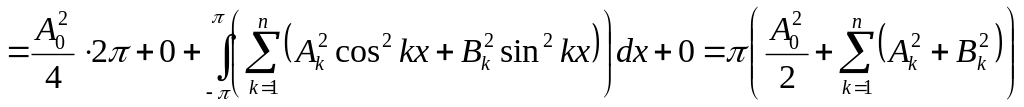
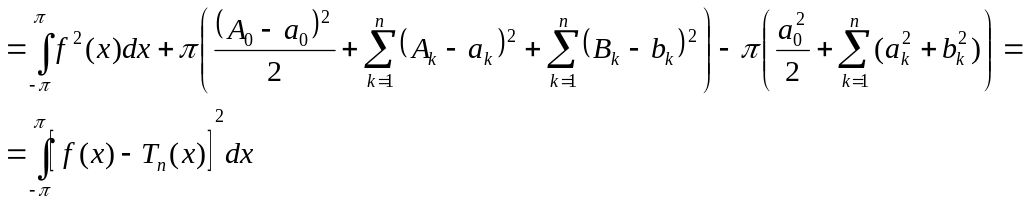
Таким образом минимум достигается, если второе слагаемое равняется нулю, т.е. и для всех k. Значит при

След.1. Из полученного равенства при получаем

откуда

Данное неравенство верно при любом n. Переходя к пределу по , получаем неравенство Бесселя

справедливое для любой интегрируемой функции.

След.2. Если ряд Фурье функции f(x) сходится в среднем к самой функции, то . Из соотношения (4) получим при этом равенство Парсеваля:

Интегральная форма частичной суммы ряда Фурье функции f –

Лемма об осцилляции: пусть - интегрируемая на функ­ция, тогда

Следствие из леммы об осцилляции: если функция f(x) является -периодичной и кусочно-гладкой, то функции

являются интегрируемыми на .

Тh.2. Для -периодической кусочно-гладкой функции f(x) ее ряд Фурье сходится в каждой точке х к значению .

Функция называется кусочно-гладкой на [a;b], если она кусочно-непрерывна на [а;b] и имеет на нем кусочно-непрерывную производную. Кусочная непрерывность - это непрерывность всюду на [a;b], кроме ко­нечного числа точек, в которых имеются конечные односторонние пре­делы.

Теорема 3. Признак Дини. Если f(x) – -периодическая функ­ция, абсолютно интегрируемая на отрезке длины , точка x является точкой непрерывности или точкой разрыва первого рода функции f и при некотором интеграл сходится, то ряд Фурье функции f сходится в точке х к значению (*)

След. Ряд Фурье кусочно-дифференцируемой на функ­ции f сходится в каждой точке интервала к значению (*), а в точках и - к

Опр. Пусть функция f(x) определена и непрерывна на отрезке . Для каждого назовем модулем непрерывности функции f(x) на сегменте [a;b] величину .

Опр. Функция f(x) принадлежит на отрезке классу Гельдера с показателем если модуль непрерывности функции f на отрезке [а;b] имеет порядок .

Тh 4. Если функция f(x) принадлежит на отрезке клас­су Гельдера с каким угодно показателем и если, кроме того, , то тригонометрический ряд Фурье функции f сходится к этой функции равномерно на отрезке .