12(1). Интеграл Римана.
1. Понятие интеграла Римана.
Пусть на [a;b]
задана функция f(x)
(рис.1) Разобьем [a;b]
на части точками деления
,
совокупность которых – Т – назовём
разбиением
отрезка [a;b].
Пусть
- длина k-го
отрезка разбиения,
.
На каждом
,
,
выберем произвольным образом точку
.
Обозначим выбор точек
через
.
Величина
называется интегральной суммой Римана
функции f
на отрезке [a;b],
соответствующей разбиению Т и выбору
.
Опр.
Если существует предел I
интегральных сумм
при
,
не зависящий от способа деления отрезка
[a;b]
на части и выбора точек
,
то функция f
называется интегрируемой по Риману на
отрезке [a;b],
а сам этот предел –определённым
интегралом Римана функции f:
.
Геометрический
смысл определённого интеграла.
Если непрерывная на отрезке [a;b]
функция f(x)
неотрицательна на [a;b],
то интеграл
равен площади
криволинейной трапеции, образованной
отрезками прямых x=a,
x=b,
осью Ох и графиком функции f(x).
Если f(x)
изменяет знак на [a;b],
как на рис.2, то
.
Верхней (нижней) границей числового мн-ва Е наз. такое мн-во, что выполнено неравенство
Верхней (нижней) гранью числового мн-ва Е наз. наименьшая из его верхних (наибольшая из его нижних) границ. sup (inf)
и
Необходимым
условием интегрируемости
функции на
отрезке является ограниченность функции
на этом отрезке. При введенных выше
обозначениях для ограниченной на [a;b]
функции f
определены
и
– нижние и верхние грани значений f
на k-х
отрезках разбиения.
Суммы
;
называются соответственно нижней и
верхней суммами Дарбу функции f,
соответствующими разбиению Т.
Критерий Дарбу
интегрируемости функций.
Для того чтобы заданная и ограниченная
на [a;b]
функция f(x)
была интегрируема на этом отрезке,
необходимо и достаточно, чтобы
,
то есть
.
Величину
назовём колебанием
функции f
на отрезке разбиения
.
При этом
.
2. Свойства определенного интеграла докажем с помощью критерия Дарбу в терминах колебаний: для интегрируемости ограниченной функции на отрезке необходимо и достаточно, чтобы на этом отрезке
.
Для интегрируемой на [a;b] функции f и произвольной константы с функция сf интегрируема, причём
=
.
Рассмотрим
разбиение Т отрезка [a;b].
Возьмём точки
,
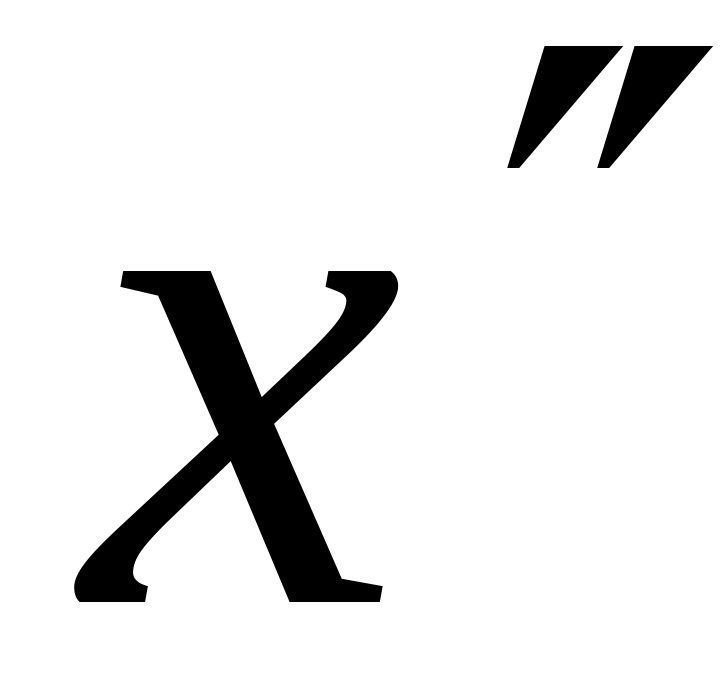из
.
Тогда
,
т.е. колебание сf(х)
на k-м
отрезке разбиения не больше, чем
,
откуда следует интегрируемость сf.
В интегральной сумме Римана функции
сf
вынесение общего множителя с и переход
к пределу при
приводит к нужному равенству.
Если f(x) и g(x) интегрируемы на [a;b], то и их сумма интегрируема на [a;b], причем
.
Пусть Т – разбиение отрезка [a;b]
на
,
,
и
,
.
Тогда
где
– колебания на
функций f
и g
соответственно. Тогда и колебание
на
функции f+g
не больше, чем
,
и по критерию Дарбу в терминах колебаний
получаем интегрируемость суммы функций.
Образуем интегральную сумму Римана функции f+g:
,
и, переходя к пределу при
,
получаем нужное равенство.
Свойства
1 и 2 говорят о линейности определенного
интеграла.
Монотонность. Если для интегрируемых на [a;b] функций f и g выполнено неравенство
,
то
,
т.е. неравенства можно интегрировать.
Образуем интегральную сумму Римана
для
:
.
Переходя к пределу при
и используя линейность определенного
интеграла, получим:
.
Аддитивность. Пусть f интегрируема на [a;b] и с (a;b).Тогда f интегрируема на [a;с] и на [с;b], причем
Пусть
и
– разбиения отрезков [a;с]
и [с;b],
тогда множество
будет разбиением [a;b].
Соответствующие колебания функции f
обозначим
.
При этом
.
Если
,
,
то
.
Верно и обратное: при
,
имеем
.
Отсюда следует интегрируемость f
на [a;с]
и на [с;b].
Образуем интегральные суммы Римана функции f на [a;с] и на [с;b]:
.
Здесь с – точка разбиения для Т. Переходя
в равенстве к пределу при
,
получаем нужное рав-во.
Классы функций, интегрируемых по Риману.
Теорема 1. Непрерывная на отрезке функция интегрируема на нем.
Теорема 2. Функция, заданная и ограниченная на отрезке, имеющая на этом отрезке конечное число точек разрыва, интегрируема на указанном отрезке.
Теорема 3. Монотонная на отрезке функция интегрируема на этом отрезке.