13(1). Первообразная и неопр-ый интеграл.

Опр1. F(x) называется первообразной функции f(х) на промежутке <a;b>, если для любого .

Геометрический смысл: первообразная - это кривая с заданным зако­ном изменения углового коэффициента. Если F(x) - первообразная для f(х), то F(x)+С - также первообразная для f ( Если F'(x)=f(х), то и (F(x) + С)' = f(x) ).

Любые две первообразные отличаются на постоянную ( если Ф(х), F(x) - первообразные для f, то для функции имеем , откуда , т.е. Ф(х) = F(x) + C ).

Опр2. Неопределенным интегралом функции f(х) назы­вается семейство всех первообразных этой функции.

Понятие определенного интеграла. Пусть на [а; b] задана функ­ция f(x). Рассмотрим разбиение Т={х₀,x₁,...,х_п} отрезка на частич­ные отрезки точками .

Пусть - длина k-го отрезка разбиения, а (Т) -наибольшая из длин отрезков разбиения. На каждом отрезке выберем произвольным образом точку . Обозначим через выбор точек . Сумма называется интегральной суммой Римана функции f(x) на отрезке [a,b].

Опр3. Если существует предел интегральных сумм при , не зависящий от способа деления отрезка [а; b] на части и от выбора точек , то этот предел называется определенным интегралом функции f, а сама f(x) называется интегрируемой на отрезке [а; b].

Д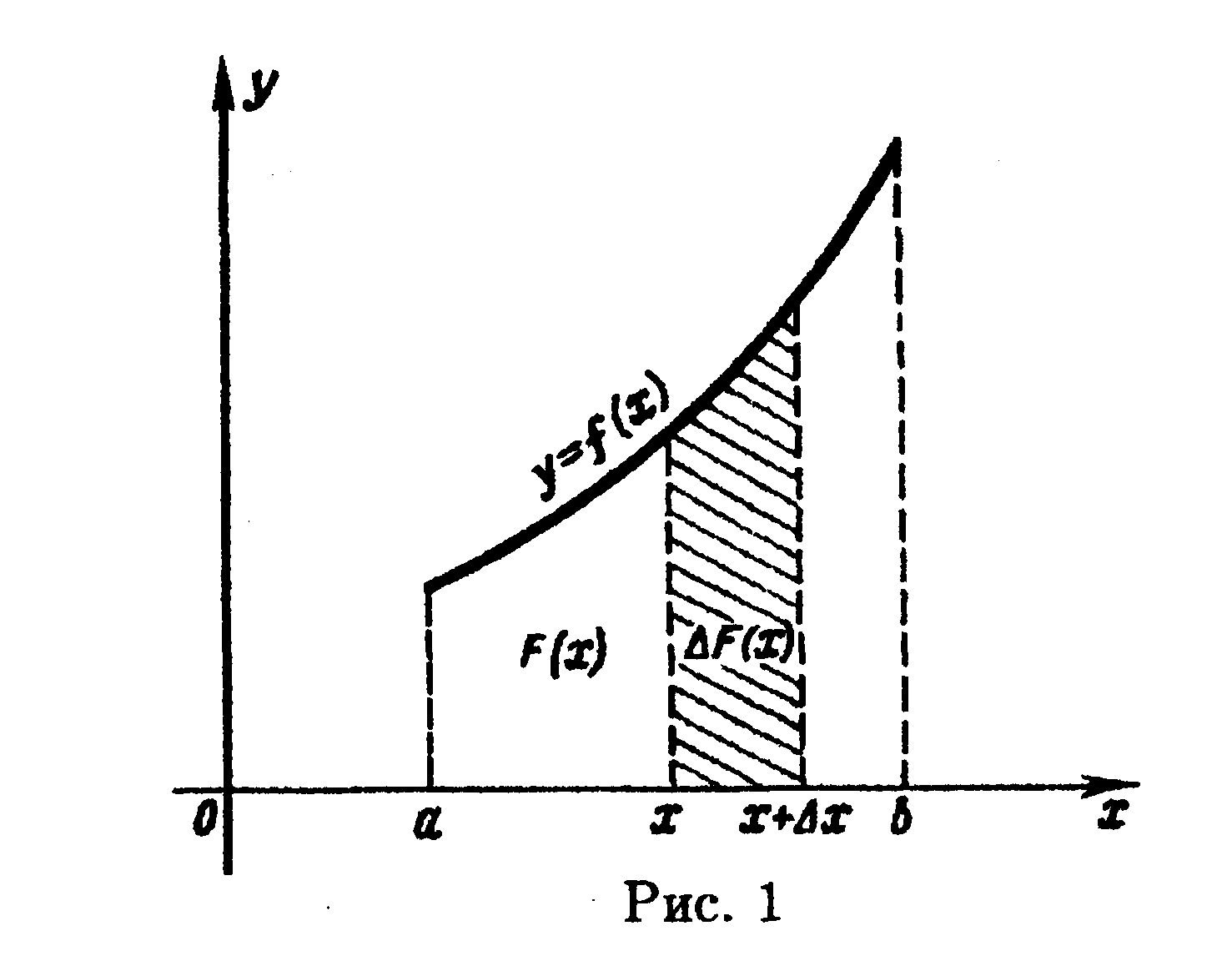 ля непрерывной неотрицательной на [а;b] функции f(х) определен­ный интеграл представляет площадь криволинейной трапеции, ограни­ченной графиком f(х), осью абсцисс и прямыми х = а, х = b. Для f(х) в каждой точке определена площадь криволинейной трапеции над отрезком [а;х], т.е. задана функция F(x), называемая интегралом с переменным верхним пределом. (Эту функцию можно определить для любой интегрируемой функции.)

Тh1. Если то интеграл с переменным верхним пределом , является дифференцируемой функцией и F'(x) = f(х).

Пусть х произвольная точка [а; b]. Зададим аргументу х приращение так, чтобы (см. рис. 1), тогда при любом располо­жении в силу аддитивности интеграла получаем равенство

По теореме о среднем (если , то существует , такая, что найдется такое или при положительном или отрицательном соответственно, что . Тогда

в силу непрерывности функции f.

Следствие. Любая непрерывная на отрезке функция обладает пер­вообразной.

Тh2 (формула Ньютона-Лейбница). Если , то где Ф(х) - какая-либо первообразная для f.

Функция является первообразной для f(x). Рассмотрим другую первообразную . Для х=а получаем , откуда С = Ф(а). Для x=b имеем , откуда и следует доказываемое равенство.

14(1). Числовые ряды.

Опр1. Числовым рядом называется символ вида

(1)

где {x_n} - числовая последовательность. Сумма первых n членов ряда называется n-й частичной суммой и обозначается S_n.

Опр2. Если существует конечный предел частичных сумм ряда , то ряд называется сходящимся, а число S-его суммой. В противном случае ряд расходится.

Необходимый признак сходимости ряда. Если ряд (1) сходится, то .

Пусть , тогда .

Другими словами: если общий член ряда не стремится к нулю, то ряд расходится.

А если общий член ряда стремится к нулю, то ряд сходится не обязан. Необходимый признак не является достаточным.

Пример:

при и .

Опр3. Числовой ряд с неотрицательными членами назовем положительным.

Тh1. Для сходимости положительного ряда необходима и до­статочна ограниченность сверху его частичных сумм.

Тh2. Если у положительных рядов , (2,3)

для всех выполняется неравенство , то из сходимости ряда (3) следует сходимость (2) (т.е. из расходимости (2) следует расходимость (3)).

Если и – частичные суммы рядов (2) и (3), то . Если ряд (3) сходится и его сумма равна , то . Но , т.е. частичные суммы ряда (2) ограничены сверху, а тогда он сходится.

Тh3 (предельный признак сравнения). Если для членов положительных рядов (2) и (3) существует

, то эти ряды сходятся или расходятся одновременно.

Признак Даламбера сходимости положительных рядов. Если для строго положительного ряда (2) при верны неравенства , то ряд (2) сходится. Если , то ряд (2) расходится.

Пусть , тогда, перемножая неравенства

, получаем

, от­куда (4)

Рассмотрим ряды

(5)

(6)

Ряд (6) сходится как сумма геометрической прогрессии со знаменателем , и тогда по неравенству (4) ряд (5) сходится и является рядом-остатком ряда (2). Следовательно, ряд (2) сходится.

Пусть при или , т.е. не стремится к нулю с ростом номера, т.е. ряд (2) расходится.

Предельный признак Даламбера. Если для строго положитель­ного ряда (2) существует конечный или бесконечный предел , то при ряд (2) сходится, при D > 1 - расходится.

Если D < 1, то найдется такое q, что D < q < 1, и по предыдущей теореме ряд (2) сходится.

Если D > 1, то при , и ряд (2) расходится.

Признак Коши - Адамара сходимости положительного ряда. Пусть для положительного ряда (2) Если К < 1, то ряд (2) сходится, если К > 1 - расходится.

Опр. Конечное число наз. частичным пределом послед., если оно является пределом его сходящейся подпослед.

Опр. Наибольший из частичных пределов послед. наз. верхним пределом последовательности.

Признак Коши сходимости положительного ряда. Пусть для положительного ряда (2) Если К < 1, то ряд (2) сходится, если К > 1 - расходится.

Признак Лейбница сходимости знакопеременного ряда. Если модуль общего члена знакопеременного ряда , где

с возрастанием номера монотонно стремится к нулю, то ряд (7) сходится.

В частичных суммах ряда (7) с четными номерами навесим скобки:

Так как по условию монотонно убывает, то разности во всех скобках положительны и возрастают. Перепишем эту же сумму по-другому:

Так как и здесь в каждой скобке выражение положительно, то, очевидно,

Итак, последовательность частичных сумм {S_2k} монотонно возрас­тает и ограничена сверху, т.е. имеет предел. Пусть

Так как

то и , т.е. ряд сходится.