15(1). Функциональные посл-ти и ряды.
Опр.1.
Заданные
на мн-ве Е ф-ии fn(x),
n
= 1,2,...
образуют
функ-ую посл-ть. Если для точки
числовая посл-ть {fn(х0)}
сходится,
то функ-ая посл-ть {fn(x)}
наз-ся
сходящейся
в
этой точке.
Мн-во всех точек из Е, в кот. функ-ая посл-ть сходится, наз-ся обл. сходимости этой посл-ти.
Т.о.,
каждому х
из
обл. сход-ти ставится в соответствие
число
,
т.е. на обл. сход-ти задается
ф-ия,
наз-ая предельной ф-ей посл-ти.
Опр.2. Для заданной функ-ой посл-ти сумма вида
(1)
наз-ся
функ-ым рядом. Если посл-ть частичных
сумм
этого ряда сходится к ф-ии S(x),
то ряд (1) наз-ся сходящимся.
Обл. сход-ти ряда (1) наз-ся обл. сход-ти функц-ной посл-ти его частичных сумм.
Пусть
задана функ-ая посл-ть
.
Говорят, что эта посл-ть сходится к
ф-ии f(x)
на
множестве Е
(поточечно),
если она сходится к f(x)
в
каждой точке мн-ва Е,
т.е.
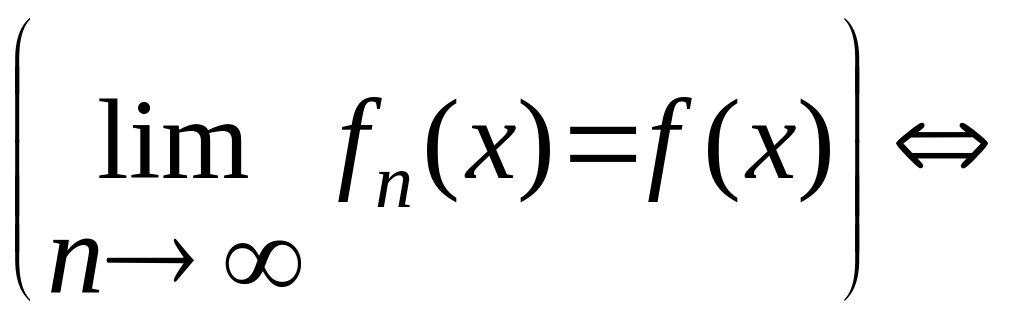
Опр.3.
Посл-ть
наз-ся равномерно
сходящейся
к ф-ии f(х)
на
мн-ве Е, если
.
Ясно, что если функ-ая посл-ть сходится равномерно на множестве Е к ф-ии f(х), то она и поточечно сходится к этой ф-ии. Обратное неверно. Т 1. Если функ-ая посл-ть {fn(x)} непрерывных ф-ий равномерно сходится на мн-ве Е к ф-ии f(х), то эта ф-ия непрерывна на Е.
T
2.
Если
и ряд
(1) равномерно на
[а;b]
сходится
к ф-ии f(x),
то
.
T
3.
Если на
[a,b]
посл-ть {fn(x)}
непрерывных ф-ий равномерно сходится
к f(x),
то
.
Ф-ии fn(x)
и f(х)
непрерывны на [a;b]
по T1,
сл-но, и интегрируемы на это отрезке.
Пусть
> 0. Из равномерности сходимости {fn(х)}
к f(х)
получаем:
а
тогда
на
основании определения предела заключаем
T4.
Если
на [а;b]
ряд (1) равномерно сходится к ф-ии f(x)
и
,
то
Th 5. Выполнение условий
1) посл-ть {fn(x)} сходится на [a;b] к ф-ии f(х);
2) сущ-ют и непрерывны на [а;b] производные f 'n(x);
3)
сход-ся равном. на
[a;b]
к ф-ии
влечет
дифф-ть f(x)
на [a,b],
причем
.
Из
усл.3) и T
3 получаем для всех х
[а;b]:
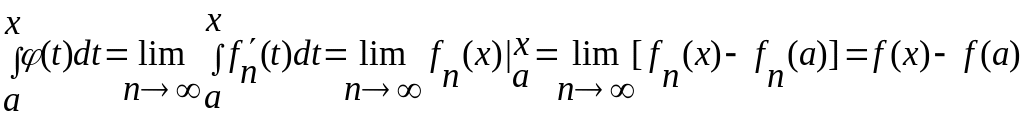(из
непр-ти ф-ий fn(x)),
откуда
Продифф-ровав это рав-во, получ. f '(х)= .
Th 6. Из усл.
1) ряд (1) сход-ся на [a;b] к ф-ии f(x);
2
)
для всех натуральных п сущ-ют и непр-ны
на
[a;b]
производные
;
3)
ряд равномерно сходится на
[a;b],
тогда
f(x)
дифф-ма на [а;b],
причем
16(1). Степенные ряды.
Определение 1. Функциональный ряд вида
(1)
где
- постоянные числа,
x
– аргумент,
называется степенным
рядом.
a
– центр сходимости ряда,
- его коэффициенты.
Теорема 1 (Коши
– Адамара).
Дан ряд (1) и
. Если
,
то ряд (1) сходится абсолютно в интервале
и расходится при
.
Если K=0,
то ряд сходится абсолютно на
всей прямой; если K=∞, то ряд сходится абсолютно только в центре сходимости.
□ Пусть . Исследуем ряд (1) на абсолютную сходимость по признаку Коши – Адамара:
(при этом использовано
свойство верхнего предела: если для
посл-ей
неотрицательных чисел
то
постоянная посл-ть,
)
Итак,
(2)
Если
,
т.е. при
,
то ряд (1) сходится абсолютно, если
- расходится.
Если K=0, то из равенства (2) видно, что ряд сходится на всей оси.
Если K=∞,
то при
предел в (2) бесконечен, и ряд (1)
расходится. ■
Опр. 2.
В условиях теоремы 1 число
называется радиусом сходимости степенного
ряда (1), а интервал
- интервалом сходимости этого ряда.
Теорема 2.
Степенной ряд (1) с R>0
при любом
сходится равномерно на
.
□
Пусть
,
тогда по теореме Коши – Адамара ряд (1)
абсолютно сходится в точке
,
т.е. сходится ряд
(3)
Для любого
имеем
тогда
Следовательно, ряд (1) мажорируется на
сходящимся положительным рядом (3), т.е.
по признаку Вейерштрасса ряд (1) сходится
на
.
■
Следствие
(теорема Абеля).
Степенной ряд (1) сходится равномерно
на любом отрезке
□ Всегда можно
указать такой отрезок
,
что
при этом по теореме 2 ряд сходится
равномерно на
,
следовательно, и на его части -
.
■
Теорема 3. Сумма f(x) степенного ряда (1) R>0 непрерывна внутри интервала сходимости.
Теорема 4. Внутри интервала сходимости степенной ряд (1) с R>0 можно почленно интегрировать и дифференцировать.