9(1). Т. Вейерштр. Об огр-сти.

Верхней (нижней) границей числового мн-ва Е наз. такое мн-во, что выполнено неравенство

Верхней (нижней) гранью числового мн-ва Е наз. наименьшая из его верхних (наибольшая из его нижних) границ. sup (inf)

1ая Т. Вейерштр. Ф-ция, непререрывная на отрез­ке, ограничена на нем.

2ая Т.Вейер-са. Ф-ция, непр. на отрез­ке, достигает на нем наименьшее и наибольшее значения.

Надо показать, что для ([а;b]) найдутся точки и этого отрезка, в которых

, .

Заметим, что числа и существуют, т.к. по 1Т Вейерштр. ф-ция огр.

Предположим, что на [а;b] ф-ция не принимает значения М, тогда [а;b] . Рассмотрим ф-цию , определенную на [а;b]. Эта ф-ция непр. на [а;b], т.к. в каж­дой точке этого отрезка , а тогда по 1Т Вейер­штр огр. на [а;b]: , откуда для всех [а;b], что противор. опр. М как верхней грани мн-ва значений ф-ции .

1 Тh Больцано - Коши. Если непр. на отрез­ке ф-ция принимает на концах отрезка значения разных знаков, то внутри отрезка найдется точка, в которой ф-ция равна нулю.

2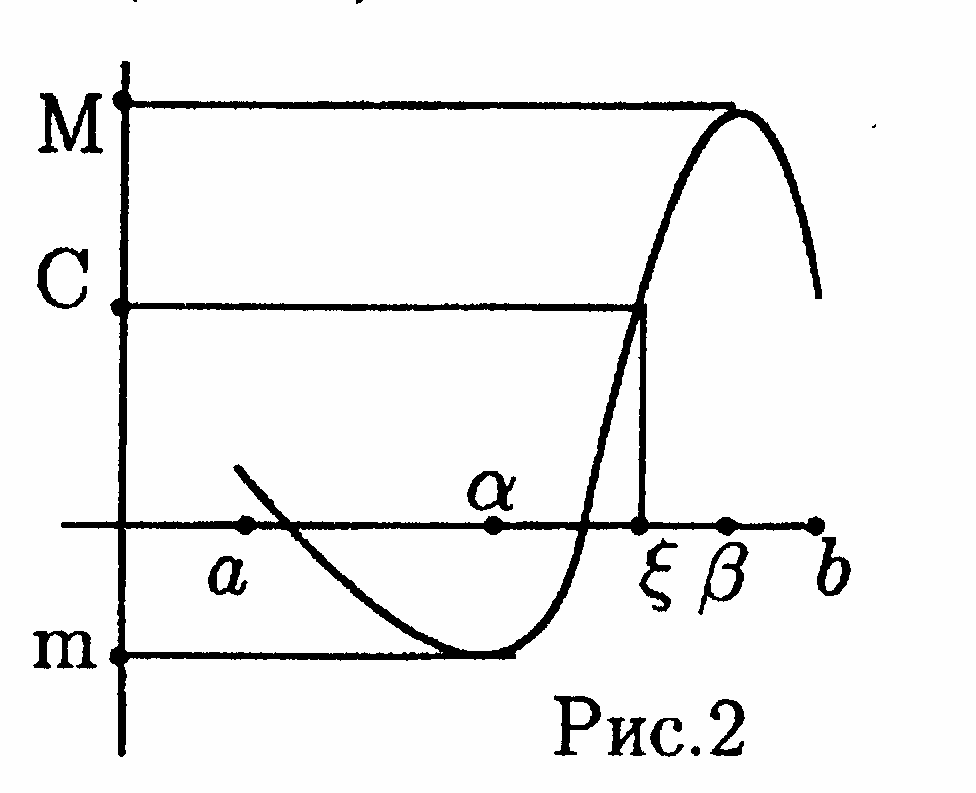 Th Больцано-Коши. Ф-ция, непр. на от­резке,

принимает все значения между наим. и наиб..

По 2th Вейерштр. ф-ция, непр. на отрезке, достигает на нем наим.(m) и наиб.(М) значения в некото­рых точках и (рис. 2).

Для произв-го найдем точку , в кото­рой . Рассм. ф-цию , заданную и непр. на . Т.к. и , то по 1Th Больцано-Коши : , или .

Функция это закон соответствия между мн-вами M и N, при котором каждому ставится в соответствие единственный элемент .

Если биективно отображает множество М на множество N, то на N определено обратное отображение .

Справедлива теорема существ-я обратной ф-ции. Если сюръективно отобра­жает М на N и возрастает на М, то на N определена возраст-щая обратная ф-ция.

Тh о непр-сти обратной ф-ции на отрезке. Пусть возрастающая на отрезке ф-ция у=f(x) непр. на , тогда на отрезке определена возрастающая непр. обратная ф-ция.

Вопрос: Как связаны графики прямой и обратной ф-ций? Ответ:Графики и совпадают и симметричны относительно прямой (рис.4).

10(1). Дифф-мость числовой ф-ции.

Пусть f(x):(а,b)→R и . Зададим приращение Δх так, чтобы . Велич. наз-ся приращением ф-ции f в точке , соответствующим приращ-ю ар­г-та Δх.

Опр.1 Если приращение ф-ции в т. может быть записано в виде (1)

где А( ) - число, не зависящее от Δх, а при Δх→0, то ф-ция f наз. дифф-мой в точке , число А( ) -производной ф-ции f в этой т. (обознач.- ), а велич. - дифференциалом ф-ции f в точке (обознач.-df(x₀)).

Так как в (1) оба слагаемых - бесконечно малые велич. при Δх→0 (придел = 0), причем - бесконечно малая более высокого порядка, чем первое слаг. , которое линейно относительно Δх, то диф­ф-лом назовем главную линейную часть приращения ф-ции в т.

Производную функции f в т. - предел отношения приращения ф-ции к приращению арг-та при стрем­лении последнего к нулю: (2)

Если ф-ция дифф-ма в каждой т. некот. мн-ва Е, то на этом мн-ве задана ф-ция .

Т1. Приращение ф-ции f в точке х₀ представимо в виде(1), если только в т. х₀ сущ-ет конечная производная в смысле опр.(2).

Из (1) . Переходя к пределу по Δх→0, имеем , т.к. при Δх→0.

Пусть ,тогда где при Δх→0, т.е. (1).

Следствие. Полагая Δх:= dx, получим:

df(x₀)= dx,

Тh2.Если ф-я диф-ма в т.,то она непр-на в этой т.

Обратное утвержд. неверно: непрер. ф-ции в т. не гарантирует ее дифф-ти.

Г еометрический смысл производной. Пусть f(x):(а,b)→R, и т. М(х₀+Δх,f(x₀+Δх)), М₀(х₀,f(x₀)), принадлежат графику ф-ции. Прямая М₀М - секущая.

Допустим, что в т.М₀(х₀,f(x₀)) сущ-ет касательная к гр-­ку ф-ции f(х), т.е. предельное положение секущей М₀М при М→ М₀ по графику ф-ции(рис.1).

Если k' = tgβ- угловой коэфф-т секущей, a k = tgα - угловой коэфф-т касательной, то, т.к. при М→ М₀ имеем β→α и, Δх→0, получим т.е производная

ф-ции в т. явл. угловым коэфф-том касат-ной к гр-ку ф-ции в этой т.

Прав-ла дифф-я суммы, произвед.и частного ф-й

Если в т. х сущ-ют производные ф-ций f и g, то сущ-ют производные суммы и произвед. этих ф-ций, а при g(x)≠0 –и их частного, причем

Док-м,2).Обознач.

так как (из T 2).

T3. Дифф-ние обратной ф-ции

Если ф-ция х = f(y) задана, непр-на и строго монотонна на нек-ром интервале и дифф-ма в т. у, причем , то обратная ф-ция у = f ^-1(x) дифф-ма в т. х = f(y) и

Тh 4. Дифф-ние сложной ф-ции

Пусть задана сложная ф-ция у=f[φ(х)]=F(x), x - основной ее аргумент, z=φ(х)- промежуточный. Если ф-ция z=φ(х) имеет производную в т. х, а ф-ция у = f(z) дифф-ма в т. z=φ(х), то сложная ф-я F(x) дифф-ма в т. х, причем

Зададим основному арг-ту х приращение Δх, тогда z=φ(х) получит приращение Δz, сложная ф-я получит приращение Δy. По усл, ,т.е.

где →0 при Δz →0. (4)

Рав-во (3) написано в предположении, что Δz≠0, а рав-во (4) верно и в том случае, когда Δz=0: при этом . Разделим (4) почленно на Δх≠0: откуда, переходя к пределу по Δх→0, получим