8(1). Предел и непрерывность функции.

Опр. Точка a - предельная точка мн-ва Е, если в лю­бой ее окр-ти сущ-ет хотя бы одна точка из Е_, отличная от точки а. или:

Точка а - предельная т. мн-ва Е, если в любой её окр-ти имеется бесконечно много точек из Е\{а}.

Опр. предела ф-ции в точке по Коши. ] ф­-ция f(x) задана на мн-ве Е, Х₀- предельная т. мн-ва Е.

limf(x)=А по определению

(0< < < ).

Опр. предела ф-ции в точке по Гейне (на языке послед-тей). Пусть ф-я f(x) задана на мн-ве Е, х₀- предельная точка мн-ва Е. 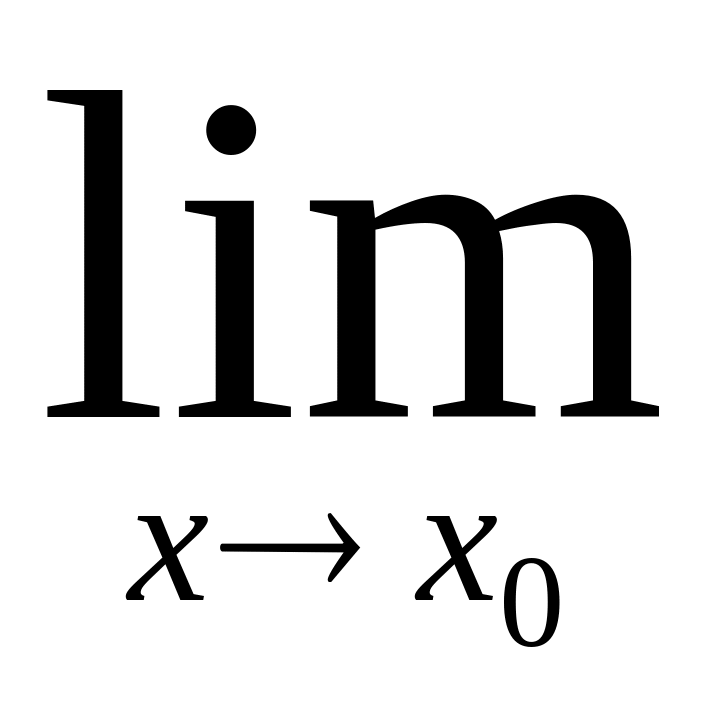f(x)=A по опр. { } E\{Х₀}({Х_n}

Опр. предела по Коши и по Гейне эквив.

Т1 (о ед-ти предела). Ф-я не может иметь в точке более одного предела.

Пусть ф-я f(x) задана на мн-ве E, х₀ - предельная т. мн-ва Е и f(x)=A, f(x)=B.

Тогда, по Гейне, имеем {f(x_n)} А и {f(x_n}} В. Но, как известно, послед-ть {f(x_n)} не может иметь более одного предела.

(Т. Если послед. имеет предел, то он единств.)

Тh2. Пусть ф-ции f₁(x), f₂(х) заданы на мн-ве Е, х₀ - предельная т. мн-ва Е и f₁(x)=A f₂(x)=В.

Тогда предел их суммы (разности, произведения) равен сумме (разности, произведению) пределов, а если еще В≠0, то и предел частного f₁(x)и f₂(x)равен частному их пределов.

T3(о переходе к пределу в нер-вах). Пусть ф-­ции f₁(х)_, f₂(x) заданы на мн-ве Е, Х₀ - предельная точка мн-­ва Е и f₁(x)=A f₂(x)=В. Если в некоторой окр-ти т. Х₀ выполнено нер-во f₁(х) f₂(x) то А В. (Если в усл. T f₁(х) f₂(x) то А В).

Т4 (о пределе промежуточной ф-ции). Пусть ф-ции f₁(х)_, f₂(x)и f₃(x) заданы на множестве Е, х₀ - предельная т. мн-ва Е и f₁(x)= f₃(x)=А. Если в некоторой окр-ти т. х₀ выполнено нер-во f₁(х) f₂(x) f₃(x) , то сущ-ет f₂(x)= А.

Т5. Пусть ф-ция f(x) задана на мн-ве Е , х₀- пре­дельная т.мн-ва Е и f(x)= А. Тогда ф-я f ограничена в некоторой окрестности точки х₀.

Т6. Пусть ф-я f(x) задана на мн-ве Е, х₀ - пре­дельная точка мн-ва Е и f(x)= А. Тогда <(>)A х f(x)>(<) .

Т7. Пусть ф-я f(x) задана на мн-ве E, х₀-пре-

дельная т. мн-ва Е. Для того чтобы f(x)= А, необх. и дост., чтобы в нек. проколотой окр-ти т. х₀ ф-ю f можно было представ.как f(x) = A +α(х), где α(х) 0 при х х₀.

Т8. Пусть ф-я z = g(x) отображ. мн-во X={х} на мн-во Z={z}, а ф-я у=f(z) отображает мн-во Z на мн-во Y={у}. Пусть х₀-предельная точка мн-ва X, z₀ -предельная точка мн-ва Z. Если g(x)=z₀ и 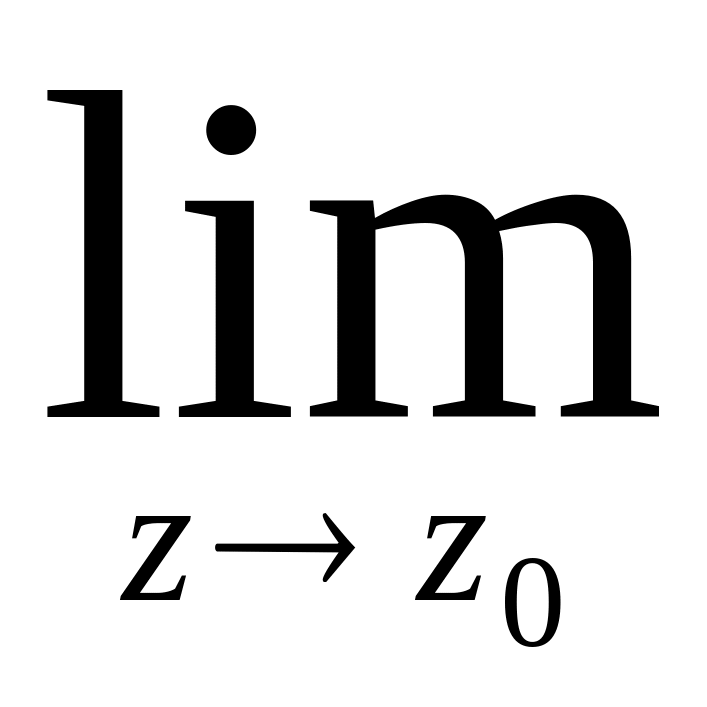f(z)= К, то f(g(x))= К.

Зададим . Т.к. f(z) = К, то

< < ). (1)

Т.к. g(x)=z₀, то по найденному σ >0

< < ) (2)

Подставим в (1) z=g(x):

(0< < < ) (3)

Тогда из (2) и (3) получаем, что

< < ),т.е f(g(x))= К.

Изолированная т. мн-ва наз. точка мн-ва, в некот. окрестности кот. не содержится других точек этого мн-ва.

Опр.непр-ти ф-ции в точке. Пусть ф-я f задана на Е, х₀ . Если х₀- изолированная точка мн-ва Е, то f непр. в этой точке. Если х₀ - предельная точка мн-ва Е, то f C(х₀) 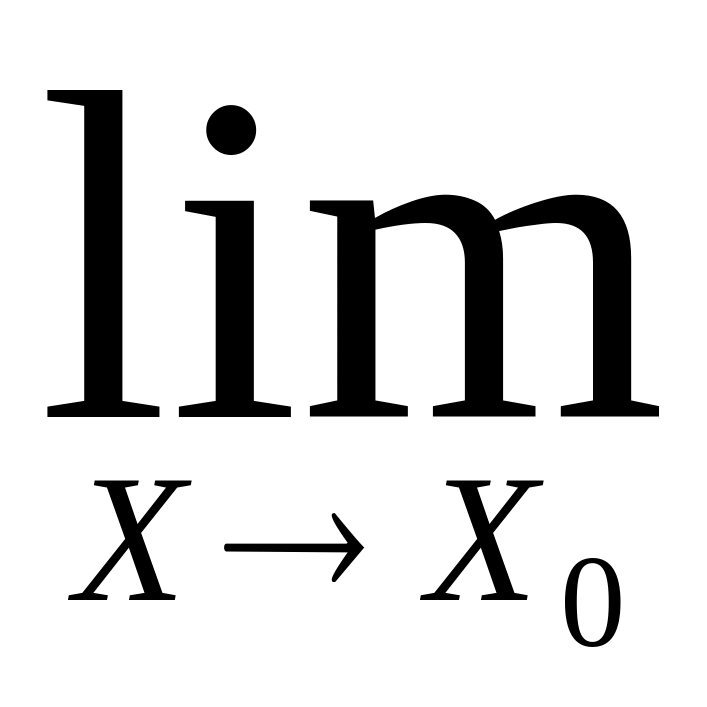f(x)= f(х₀). (4).

Усл.(4) в терминах записывается так:

f C(х₀) ( >0 < < );

В отличие от опр. предела здесь берется непроколо­тая окрестность точки х₀.

Зададим аргументу х₀ приращение так, чтобы x+ Е. При­ращением ф-ции назовем величину = f(х₀+ ) – f(х₀)

Опр. непр-ти в терминах приращений. Если ф-я f(x) задана на Е и х₀ , то f C(х₀) ( ),т.е. ф-я непр-на в точке, если бесконечно малому приращению арг-та в этой точке соответствует бесконечно малое приращение ф-ции.

Т9. Если в усл. T8 g(x) C(х₀);g(х₀)=z₀ и f(z) C(z₀),то композиция f(g(x)) C(х₀).

Опр. Ф-я непр-на на мн-ве, если она непр-на в каждой точке этого мн-ва.

Опр. левого и правого пределов, одностор. непр-ти. Пусть f задана на мн-ве Е, х₀-предельная т. Е.

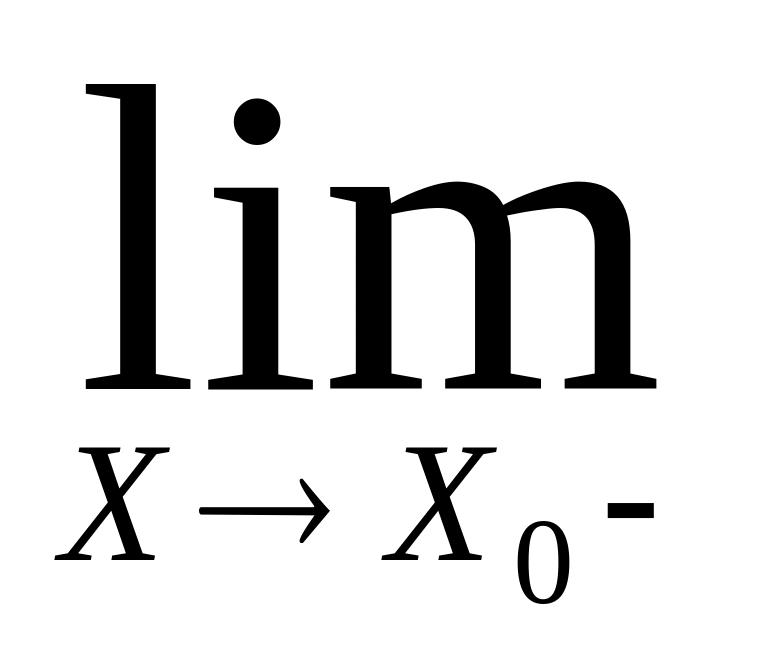f(x)=A >0 :

(0<х₀- х< < );

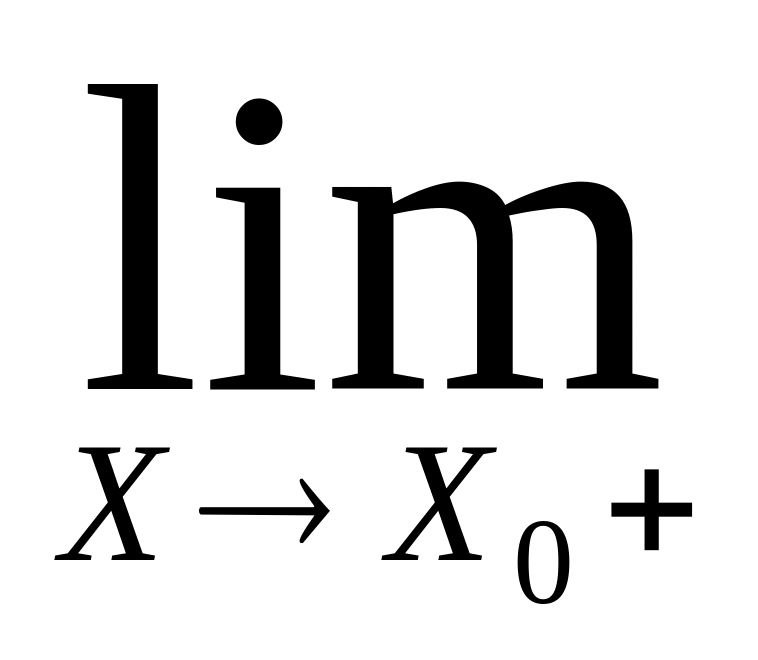f(x)=B >0 :

(0<x- х₀< < );

f C(х₀-) A= f (х₀); f C(х₀+) B= f (х₀).

Т10. f(x) f(x)= f(x);

f C(х₀) f(x)= f(x)=f(х₀).

Опр. Пусть f задана на E, Q Е, х₀ - предельная точка мн-ва Q. Число А явл. частичным пределом ф-ции f по мн-ву Q в точке х₀ , если только >0 < < );

T о частичных пределах: Для того, чтобы ф-я f(x) в точке х₀ имела пределом число A, необх. и дост., чтобы в точке х₀ сущ-ли все частич­ные пределы и все они были равны А.