Задание 4 – Построение матрицы функций модальной чувствительности
Выделение доминирующих параметров:
,
.
Из уравнения
,
где
найдем матрицу
вещественного вида:
,
.
Вычислим функции
модальной чувствительности
(
)
с помощью соотношений:
, 
;
, 
;
, 
;
, 
.
Сконструируем матрицу функций модальной чувствительности в виде функций чувствительности вещественной и мнимой частей:
,
где
По нормам столбцов выделяем доминирующие параметры:
Для выделения неблагоприятного сочетания вариаций параметров воспользуемся сингулярным разложением матрицы модальной чувствительности:
.
Используем функцию svd()
пакета Matlab.
,
,
.
Зададимся сферой
с тем, чтобы все вариации параметров
ограничить числом 0,5 – пределы применимости
теории чувствительности. Введем наиболее
неблагоприятное сочетание вариаций
параметров, задаваемое вектором:
,
а также наименее неблагоприятное сочетание вариаций параметров, задаваемое вектором:
Задание 5 – Построение закона управления для объекта, заданного интервальными элементами
Дано ВМО ВСВ НОУ с интервальными матричными компонентами в форме
получаемое с
использованием интервальной арифметики
на основе интервальной реализации
параметров
,
записываемых в форме
при следующих
граничных (угловых) значениях:
Закон управления
(ЗУ):
должен доставлять системе с интервальными
матричными компонентами
образованной объединением НОУ и ЗУ, с помощью:
- матрицы
прямой связи по входу
равенство входа
и выхода
в неподвижном состоянии при медианных
значениях параметров;
- матрицы
обратной связи по состоянию
при медианных значениях параметров
распределение мод Баттерворта с
характеристической частотой
,
которая гарантирует достижение оценки
относительной интервальности матрицы
состояния системы
не больше заданной
.
Методом модального
управления, базовый алгоритм которого,
опирающийся на решение матричного
уравнения Сильвестра и примененный к
медианным составляющим интервальных
матричных компонентов ВМО ВСВ НОУ,
дополняется контролем нормы
медианной составляющей интервальной
матрицы
спроектированной системы с последующим
вычислением оценки
,
вычислить матрицы
и
.
Формирование ВМО ВСВ интервального ОУ:
,
,
.
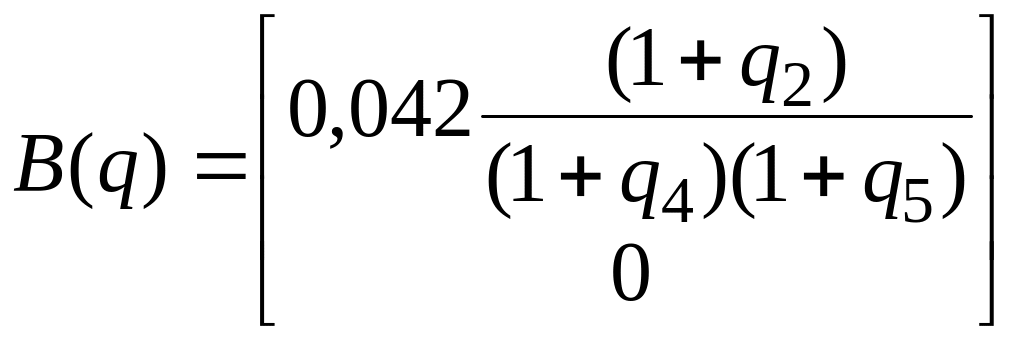Для упрощения
задачи, добьемся того, чтобы интервальной
была бы только матрица состояния. Сделаем
сигнал управления третьей переменной
состояния
и введем новое входное воздействие
.
`
Пусть управление имеет вид:
.
Новая модель ВСВ примет вид:
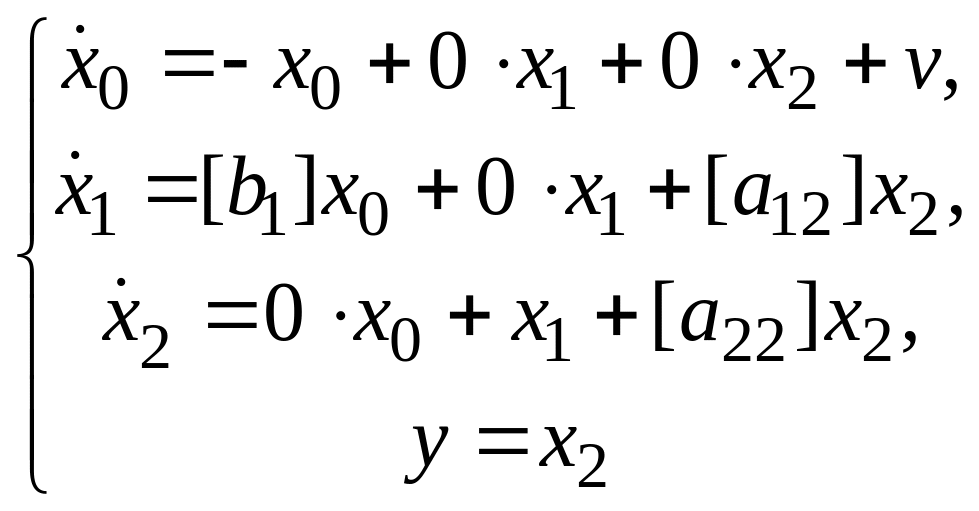
Итак, имеем новые матрицы описания объекта
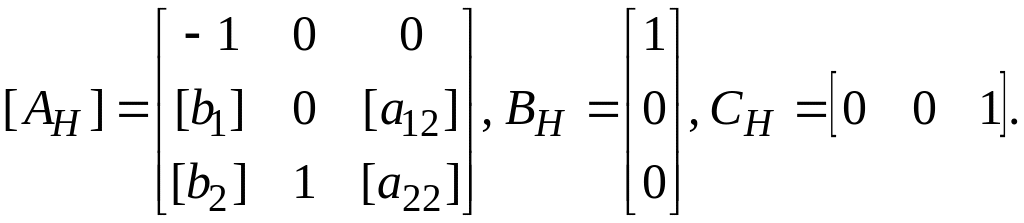
Далее определим
угловые значения матрицы
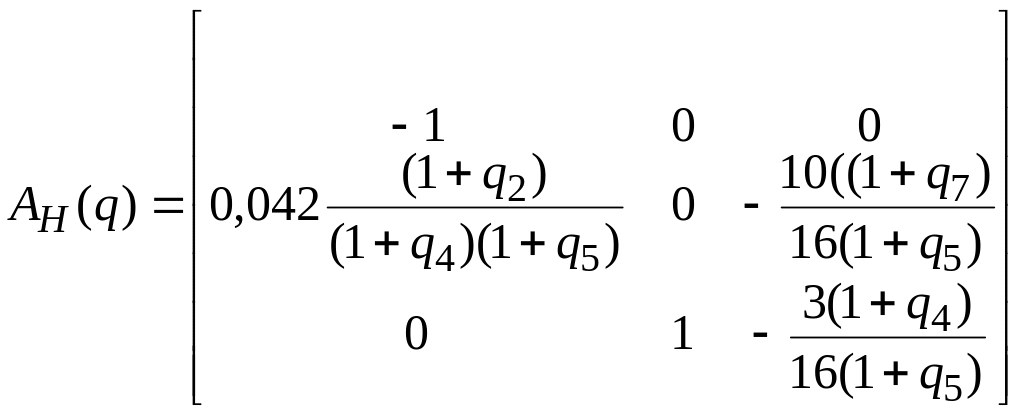
Легко видеть, что
элементы матрицы
примут максимальные значения при
,
,
а минимальные, наоборот, при
,
.
Остается лишь сравнить значения матрицы
при
,
и
,
.
Итак,
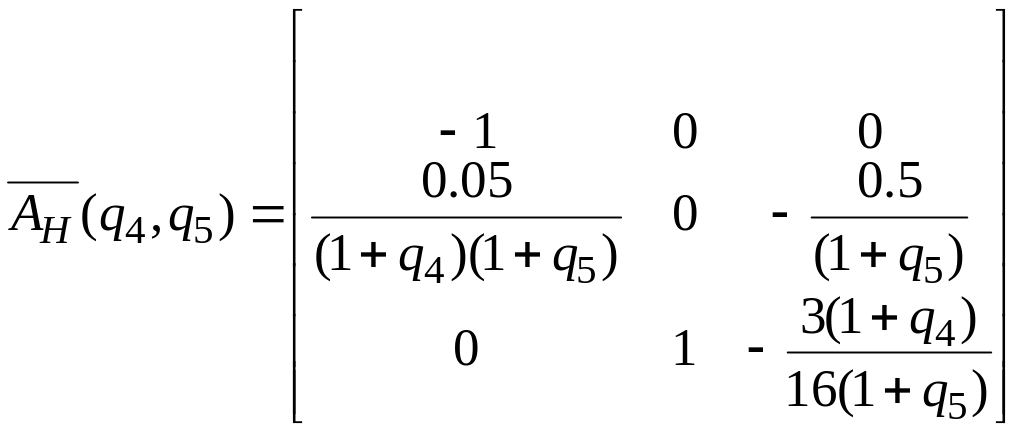
при , .
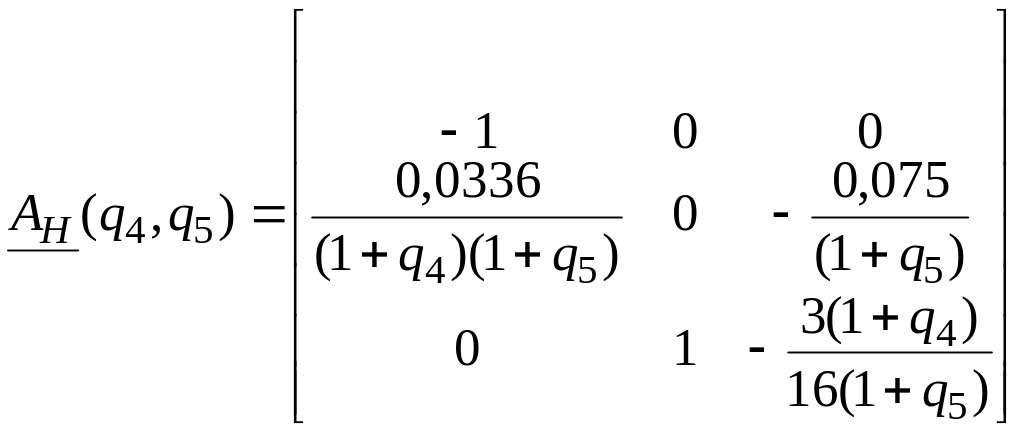
при , .
Интервальные матрицы вычисляем по правилам интервальной арифметики:
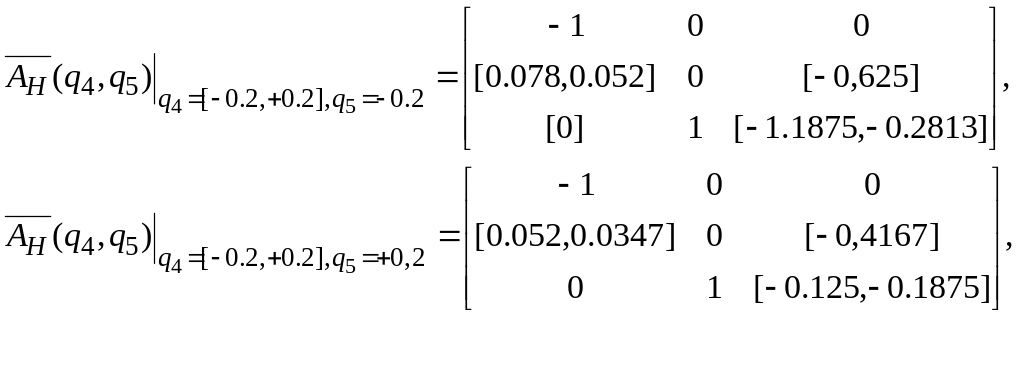
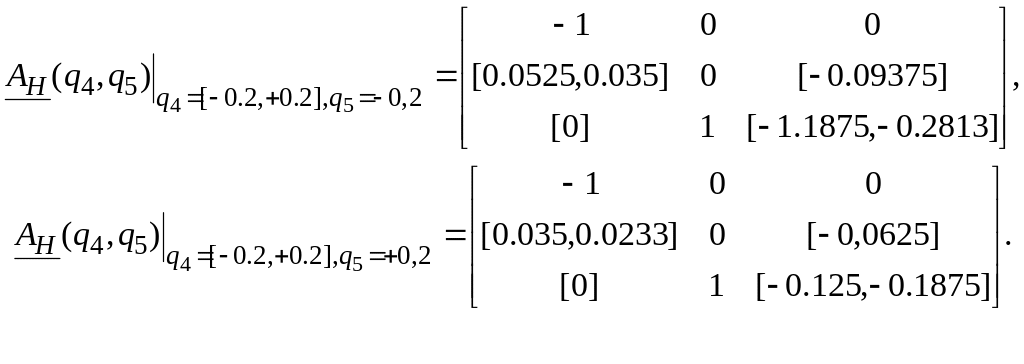
Граничные значения
матрицы
получим, скомпоновав экстремальные
значения каждой составляющей матрицы
.
,
.
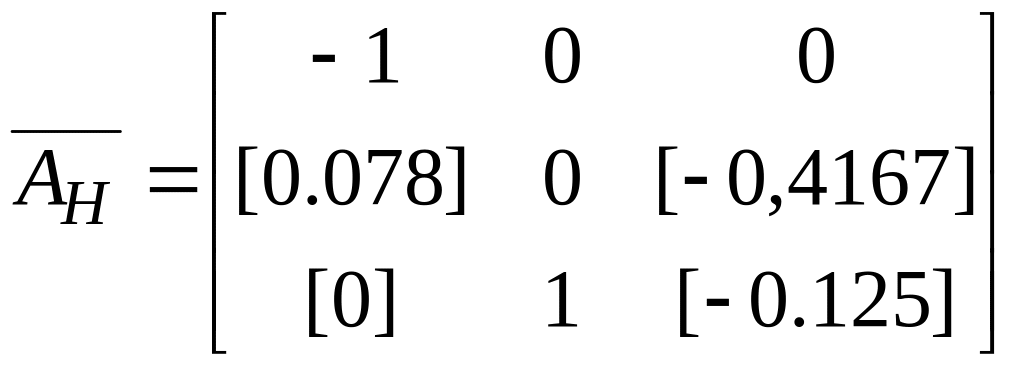Необходимо отметить,
что полученные граничные значения
интервальной матрицы
физически не реализуемы, то есть элементы
матрицы не могут принять одновременно
указанные экстремальные значения.
Другими словами, здесь неизбежно
закладывается избыточность в задании
матрицы. Это сделано формально с тем,
чтобы все реализации матрицы ограничивались
указанными значениями.
Медианное значение интервальной матрицы найдем как половину суммы угловых значений.
.
.
,
.
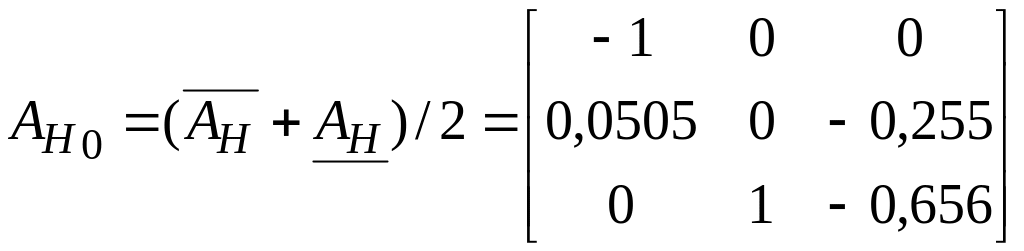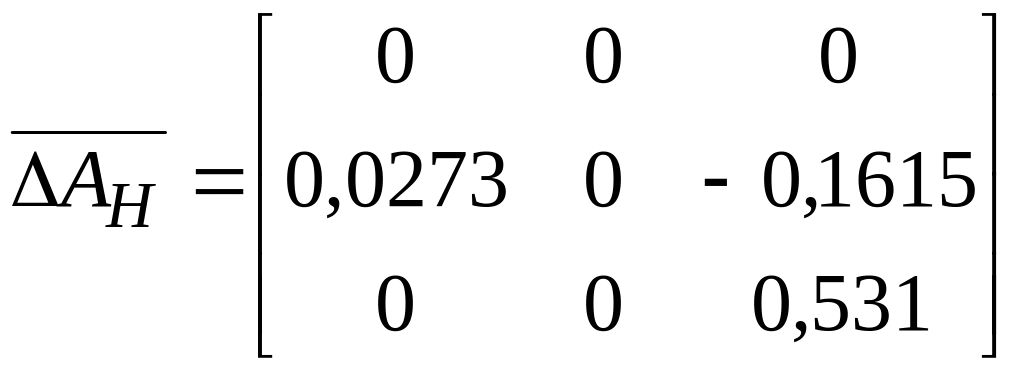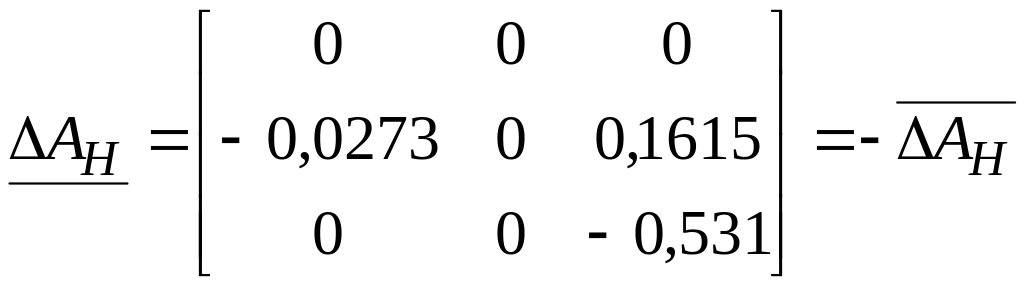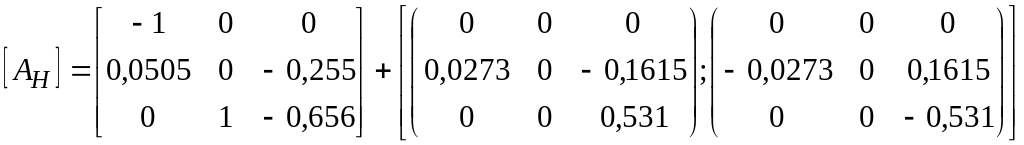
Формирование ММ:
Матрица
составляется, исходя из требуемого
распределения мод
, 
;
,
.
.
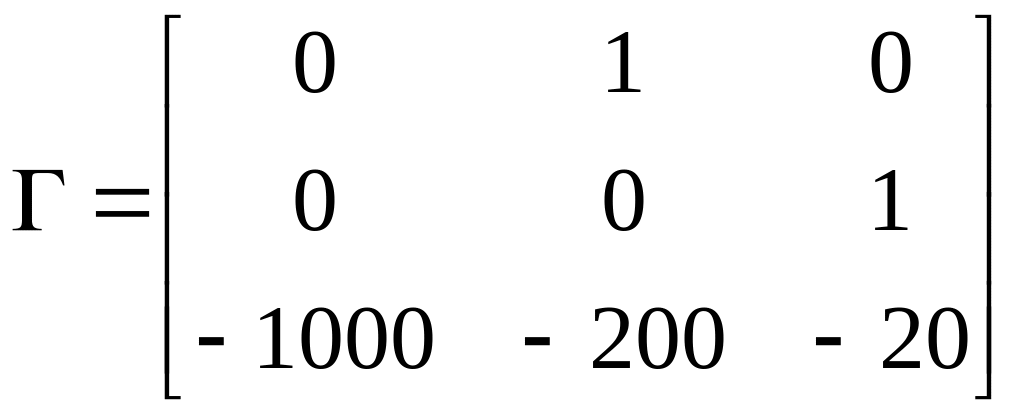Матрица
выбирается из условия полной наблюдаемости
пары
и
:
.
Решим задачу медианного МУ с помощью уравнения Сильвестра:
,
.
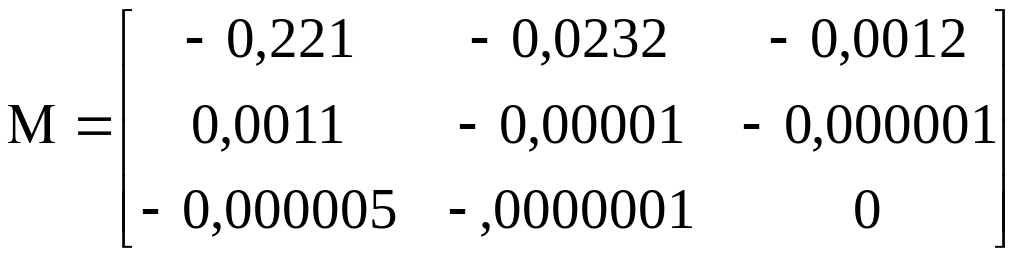Формирование
медианной составляющей
интервальной матрицы
:
,
,
Проверка выполнения
условия
:
.
Таким образом, на
частоте среза
достигается требуемая относительная
интервальность матрицы состояния
системы.
Формирование закона управления:
, 
.
, 
.
Закон управления имеет вид:
.
Переходя от
виртуального управления
к реальному
,
получим следующий математическую версию
закона управления:
.
Реализационная версия этого закона имеет вид:
.
Замечание 4.
Последняя версия будет реализуемой только в случае доступности измерению всех переменных состояния. В противном случае необходимо выстраивать наблюдатель, с целью получения оценок переменных состояния. В этом случае закон управления примет вид:
,
где и - оценки переменных состояния и соответственно.
Замечание 5.
Схема моделирования полученной интервальной системы представлена на рисунке 5.1:
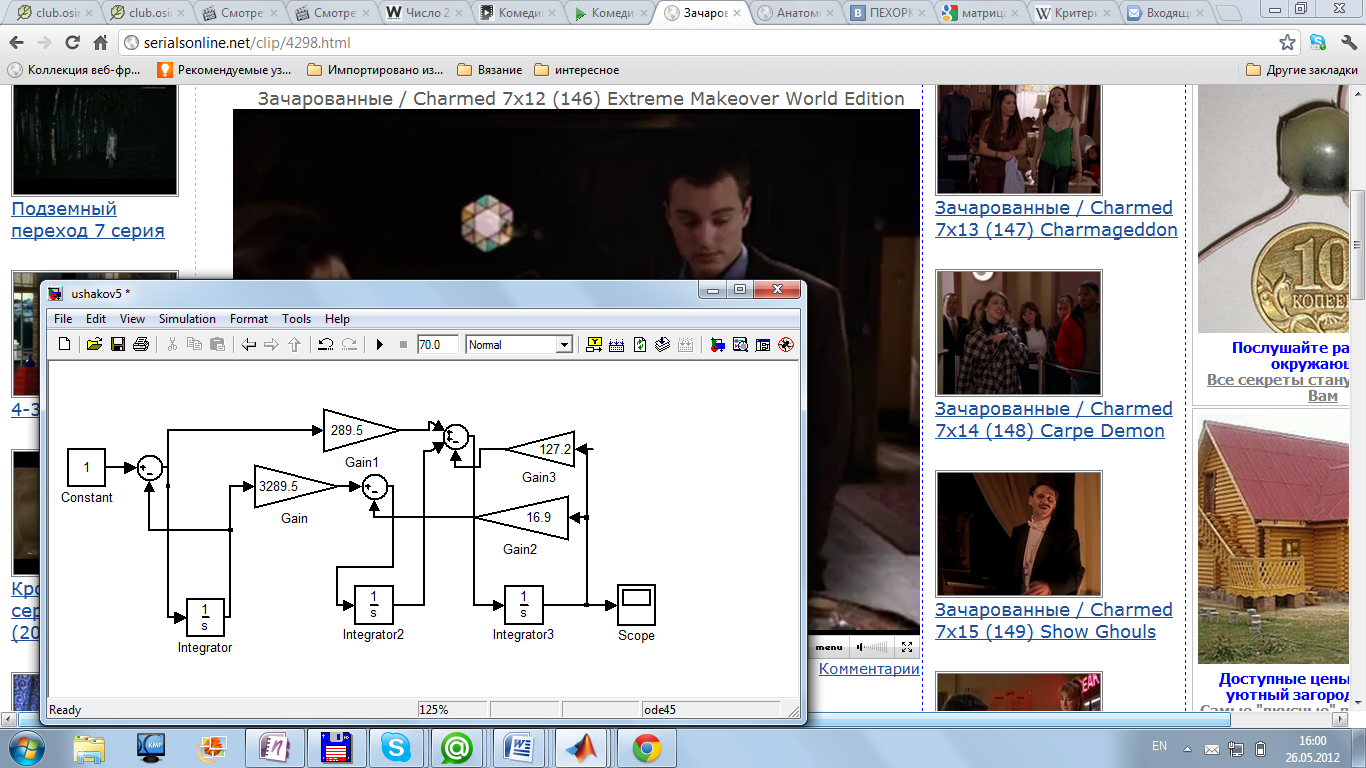
Рисунок 5.1 – Схема моделирования интервальной системы
Переходная функция интервальной системы представлена на рисунке 5.2
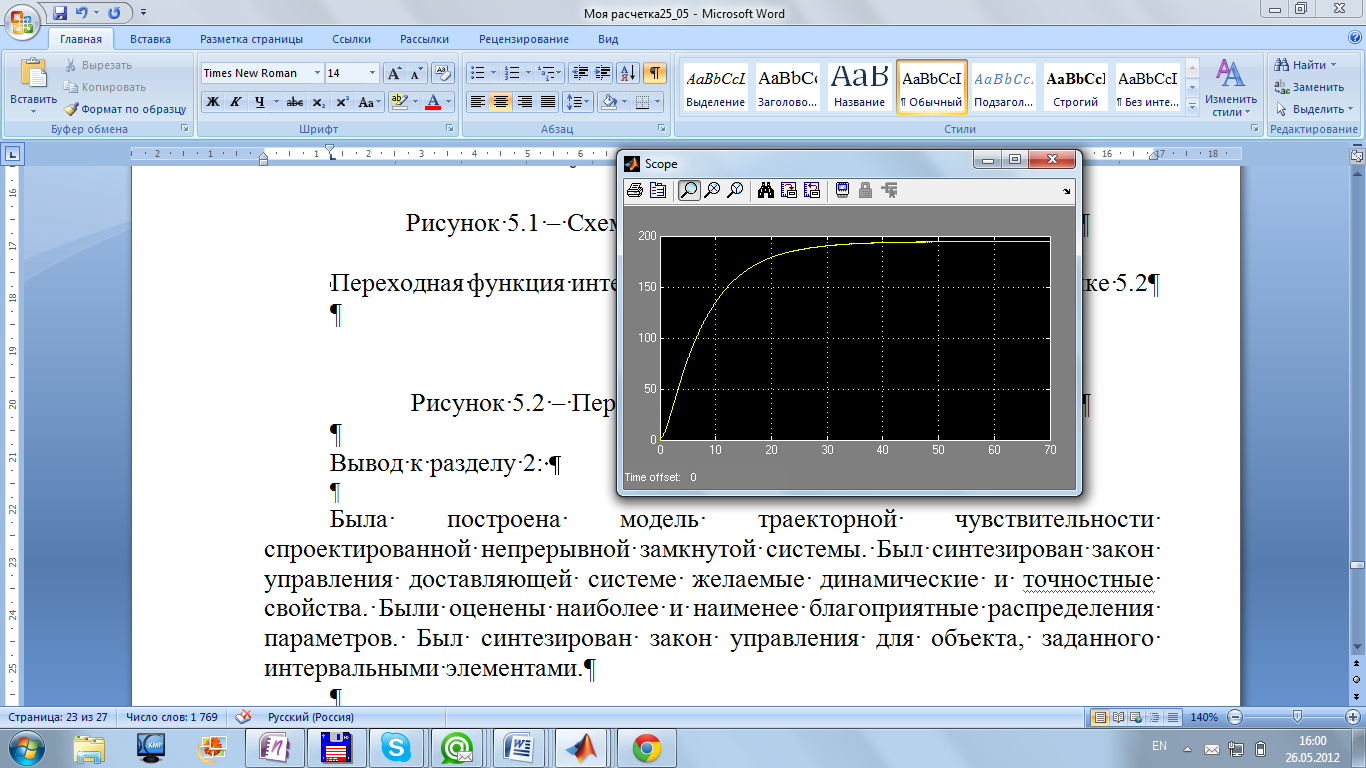
Рисунок 5.2 – Переходная функция интервальной системы
Вывод к разделу 2:
Была построена модель траекторной чувствительности спроектированной непрерывной замкнутой системы. Был синтезирован закон управления доставляющей системе желаемые динамические и точностные свойства. Были оценены наиболее и наименее благоприятные распределения параметров. Был синтезирован закон управления для объекта, заданного интервальными элементами.