Биномиальное распределение.
Биномиальное распределение
Биномиальное распределение, распределение вероятностей числа появлений некоторого события при повторных независимых испытаниях. Если при каждом испытании вероятность появления события равна р, причём 0 £ p £ 1, то число m появлений этого события при n независимых испытаниях есть случайная величина, принимающая значения m = 1, 2,.., n с вероятностями
где q = 1 — p, a
— биномиальные коэффициенты (отсюда
название Б. р.). Приведённая формула
иногда называется формулой Бернулли.
Математическое ожидание и дисперсия
величины m, имеющей Б. р., равны М (m) = np и
D (m) = npq, соответственно. При больших n, в
силу Лапласа теоремы, Б. р. близко к
нормальному распределению, чем и
пользуются на практике. При небольших
n приходится пользоваться таблицами Б.
р.
Распределение Пуассона.
Распределение Пуассона — это частный случай биномиального распределения (при n >> 0 и при p –> 0 (редкие события)).
Из математики известна формула, позволяющая примерно подсчитать значение любого члена биномиального распределения:
где a = n · p — параметр Пуассона (математическое ожидание), а дисперсия равна математическому ожиданию. Приведем математические выкладки, поясняющие этот переход. Биномиальный закон распределения
может быть написан, если положить p = a/n, в виде
Или
Так как p очень мало, то следует принимать во внимание только числа m, малые по сравнению с n. Произведение
весьма близко к единице. Это же относится к величине
Величина
очень близка к e–a. Отсюда получаем
формулу:
Равномерное распределение.
Равномерный закон распределения.
На практике встречаются случайные величины, о которых заранее известно, что они могут принять какое-либо значение в строго определенных границах, причем в этих границах все значения случайной величины имеют одинаковую вероятность (обладают одной и той же плотностью вероятностей).
Например, при поломке часов остановившаяся минутная стрелка будет с одинаковой вероятностью (плотностью вероятности) показывать время, прошедшее от начала данного часа до поломки часов. Это время является случайной величиной, принимающей с одинаковой плотностью вероятности значения, которые не выходят за границы, определенные продолжительностью одного часа. К подобным случайным величинам относится также и погрешность округления. Про такие величины говорят, что они распределены равномерно, т. е. имеют равномерное распределение.
Определение. Непрерывная случайная величина Х имеет равномерное распределение на отрезке [а, в], если на этом отрезке плотность распределения вероятности случайной величины постоянна, т. е. если дифференциальная функция распределения f(х) имеет следующий вид:
Иногда это распределение называют законом равномерной плотности. Про величину, которая имеет равномерное распределение на некотором отрезке, будем говорить, что она распределена равномерно на этом отрезке.
Найдем значение постоянной с. Так как площадь, ограниченная кривой распределения и осью Ох, равна 1, то
откуда с=1/(b-a).
Теперь функцию f(x) можно представить в виде
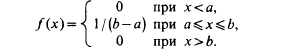
Построим функцию распределения F(x), для чего найдем выражение F(x) на интервале [a, b]:
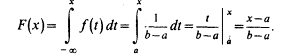
Графики функций f(x) и F(x) имеют вид:
