Формула Литтла.
Одноканальная смо с отказами.
Системы массового обслуживания с отказами. Одноканальная СМО с отказами
Наиболее простой из рассматриваемых задач в рамках теории массового обслуживания является модель одноканальной СМО с отказами или потерями.
Следует отметить,
что в данном случае количество каналов
равно 1 (
).
Этот канал принимает пуассоновский
поток заявок, интенсивность которого
равняется
. Время оказывает влияние на интенсивность:
Если заявка прибыла
в канал, который в данный момент не
является свободным, она получает отказ
и больше не числится в системе. Обслуживание
заявок осуществляется в течение
случайного времени
,
распределение которого реализуется в
соответствии с показательным законом
с параметром
:
Это говорит о том, что «поток обслуживания» является простейшим, при этом интенсивность равна . Для того, чтобы более ясно понимать о каком потоке идет речь, следует представить один постоянно занятый канал, обслуживающий заявки с потоком, интенсивность которого равна .
Определим абсолютную
пропускную способность системы
обслуживания (
),
а также относительную пропускную
способность СМО (
).
Разберем один
канал обслуживания в качестве физической
системы
, состояния которой могут быть:
-
свободен;
- занят.
ГСП системы продемонстрирован на рис. 5.6, а
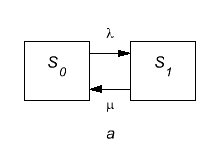
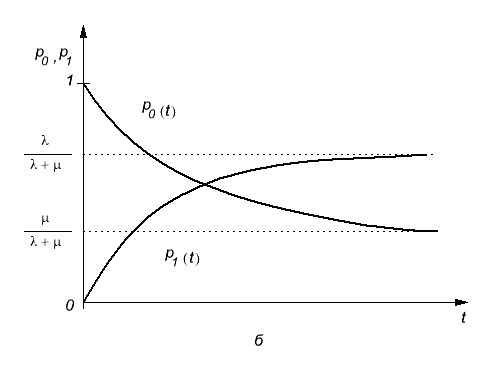
Рис. 5.6. ГСП для одноканальной СМО с отказами (а);
график решения управления (5.38) (б)
Поток с интенсивностью, равной способствует переходу системы .
и
представлены
в качестве вероятностей состояний.
Таким образом, для любого момента
:
(5.36)
Запишем дифференциальные уравнения Колмогорова для вероятностей состояний, используя правило, обозначенное выше:
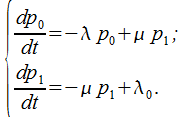(5.37)
Из двух уравнений
(5.37) одно можно не рассматривать, поскольку
и
имеют
между собой связь, которая выражена в
соотношении (5.36). Принимая это во внимание,
а также не используя второе уравнение,
в первом вместо
применим
:
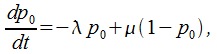или
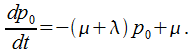(5.38)
По причине того, что в исходный момент канал не является занятым, уравнение может быть решено в соответствии с начальными условиями:
Для линейного
дифференциального уравнения (5.38) с одной
неизвестной функцией
без
проблем может быть найдено решение не
только для простейшего потока заявок,
который предполагает, что
,
но и для потока, интенсивность которого
способна изменяться с течением времени.
Решение для первого
случая:
На рис. 5.6, б показана
зависимость величины
,
которая дополняет до единицы
.
Очевидно, что
вероятность
канал
не будет занят или что заявка, которая
появилась в системе в момент
покинет
ее обслуженной. Таким образом, для
данного момента времени
среднее
отношение количества обслуженных заявок
к количеству заявок поступивших можно
выразить так: .
В переделе, если
и
сформируется процесс обслуживания,
предельное значение относительной
пропускной способности будет равно:
Имея данные об
относительной пропускной способности
,
можно без проблем определить абсолютную
. Связь между ними представлена в виде
соотношения:
В пределе (при
)
сформируется пропускная способность,
которая будет равна:
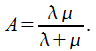
Относительная
пропускная способность системы
известна
(вероятность того, что поступившая в
систему заявка во временной отрезок
буде обслужена каналом), определим
вероятность отказа:
или среднюю долю необслуженных заявок среди тех, которые находятся в системе. При:
