6. 3. Змішані стратегії

Наявність у грі сідлової точки дає можливість визначити необхідні оптимальні стратегії. Але деякі ігри не завжди мають сідлові точки, тобто максимінно-мінімаксні стратегії неоптимальні. Це призводить до того, що кожний із гравців може поліпшити своє становище, вибравши іншу стратегію. У даному випадку виникає потреба у використанні змішаних стратегій.

Змішані стратегії - це математична модель можливої й гнучкої тактики гравця, при якій супротивний йому гравець не може знати наперед ситуацію, з якою йому прийдеться зіткнутись у грі, тому перед кожною партією проводиться випадковий вибір однієї з чистих

стратегій з допомогою деякого механізму, який здійснює цей вибір із визначеними й наперед заданими ймовірностями.

Розглянемо гру двох осіб, матриця платежів якої має розмірність п х т. Нехай гравець А має п стратегій, а гравець В - т стратегій. Позначимо через р = (рі , р₂ ,...рП) і ^ = (ді, д2,,-,Ят) вектори ймовірностей, з якими гравці А та В відповідно вибирають свої чисті стратегії. Оскільки ці стратегії за умовою гри повністю вичерпують можливі ходи гравців А і В, то вони утворюють повну групу подій.

п т

Тому має місце: X Р, = X . (6.2)

і=1 ]=1

Якщо аі] - (і, ])-й елемент матриці гри, то платіжна матриця має вигляд

Відповідно до основної теореми теорії ігор кожна скінченна гра має хоч би один розв'язок, який визначає певна змішана стратегія.

			Ві	В2	...	Вт
			Яі	42	...	^т
А	Аі	Рі	аіі	аі2	...	аіт
	...	...	•		...	•
	Ап	Рп	апі	ап2	...	апт

Методика визначення розв'язку гри при змішаних стратегіях в основному також грунтується на використанні критерію мінімаксу. Різниця полягає в тому, що гравець А вибирає Рі так, щоб максимізувати найменший сподіваний виграш (математичне сподівання) по стовпцях, тоді як гравець В вибирає з метою мінімізації найбільшого сподіваного виграшу по рядах. Математично критерій мінімаксу для змішаних стратегій описується наступним чином. Гравець А вибирає стратегію Аі, яка дає

\

(6.3)

тах \ тІПІ X ^а1 Рг ^, X ^аг 2 Рг ^ X ^агтРг

і=1

і=1

і=1

а гравець В вибирає стратегію В_}, яка дає

Ґ т т т Л

X ^а1 Д]^, X ^а 2 Я]^,...^, X ^ап]Ч]

(6.4)

тах

тіп

V]

V] =1 ] =1 ] =1 ^

Ці величини визначаються відповідно як сподівані максимінні та мінімаксні платежі. При цьому має місце співвідношення:

>

Мінімаксний сподіваний програш

Максиміний сподіваний виграш

Якщо рі і відповідають оптимальним розв'язкам, тобто виконується строга рівність, то результуюче значення дорівнює сподіваному (оптимальному) значенню гри. Якщо р* і д * оптимальні

розв'язки для обох гравців, то кожному елементу платіжної матриці відповідає ймовірність р_г д_;. Отже, оптимальне сподіване значення

(ціна) гри

п т

^у* = ТТ^а«РІя*. ⁽⁶.⁵⁾

і =і І =і

Для знаходження оптимальних стратегій в іграх двох осіб з нульовою сумою можна використати графічний метод (для ігор виду 2 х т або 2 х п), а також привести задачу до лінійного програмування.

6.4. Графічний метод розв'язку ігор виду 2 х т і п х 2

Розглянемо гру виду 2 х т, яка не має сідлової точки.

В

		Ві	В2		Вт
		Чі	42	• • •	Цт
Аі	Рі	аіі	аі2	...	аіт
А А2	Р2=і-Рі	а2і	а22	• • •	а2т

Оскільки гравець А має дві стратегії (А₁ і А₂), то р₂ = і- р₁. Знайдемо сподівані виграші (математичне сподівання гравця) А залежно від чистих стратегій гравця В:

^Мі ⁽Рі ) = ^аіі • Рі + ^а2і • Р2 = ^(аіі ^{- а}2і )Рі + ^а2і ^, У = ^{1, т} . ⁽⁶.⁶⁾ Отримані результати представимо у вигляді табл. 9.2.

Таблиця. 62.

Чисті стратегії гравця В	Сподівані виграші гравця А
і	(аіі-а2і)Рі +а2і=Мі (Рі)
2	(аі2-а22)Рі +а22=М2 (Рі)
•	•
т	(аіт- а2т)Рі +а2т=Мт (Рі)

Із таблиці 6.2. випливає, що сподіваний виграш гравця А М^(р₁) лінійно залежить від р₁ і являє собою пряму лінію.

Мета гравця В полягає в мінімізації виграшу гравця А за рахунок

вибору своїх стратегій, тобто М (р₁) = тіп |М_у (р₁)}. На рис. 6.1 точка

і

М* означає значення М(р*), яке дістали при р₁ = р*. Ціна гри

V = М (р*). Таким чином, графічно визначається оптимальна змішана

* . . „

стратегія р₁ = р₁ першого гравця і пара частих стратегій другого гравця, які в перетині утворюють точку М* (на рис. 6.1 це відповідає ІІ і ІІІ стратегіям гравця В).

Розв'язавши систему рівнянь М_} (р₁ ) = V(і = 2,3), знайдемо

точне значення р* і V. Після цього, надавши = 0 для тих і, для яких

*

М_і(р₁) не утворюють точку М, можемо знайти значення для тих і, для яких М(р₁ ) утворюють точку М, розв'язавши систему

^а12 Ч 2 + ^а 22 Чз = ^^ і . ⁽⁶.⁷⁾

^а13 Ч 2 + ^а 23 Яз = ^V

Рис. 6.1

Приклад 6.2 На основі наявного добового обсягу сировини підприємство має можливість випускати два види продукції, яка швидко псується. Прибуток підприємства залежить від обсягу реалізованої продукції кожного виду, яка в свою чергу залежить від погоди.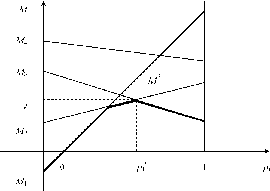

Реалізація першого виду продукту вища за теплої погоди, другого - за прохолодної. Стан погоди можна розглядати як такі стратегії природи: день пекучий сухий, пекучий вологий, теплий сухий, теплий вологий, прохолодний сухий, прохолодний вологий. Відома матриця прибутку (тис. грн.) підприємства за кожним видом продукції залежно від стану погоди:

[12 9 7 5 4 2"

_ 3 5 6 8 9 10_.

За допомогою графічного методу знайти оптимальні стратегії по організації випуску продукції підприємством.

Розв язання. Побудована гра не має сідлової точки в чистих стратегіях, тому для визначення оптимальних стратегій можна скористатися графічним методом. Стратегіями підприємства є виробництво продукції першого або другого виду. Будемо вважати підприємство першим гравцем, а природу - другим. Позначимо через р₁ імовірність використання своєї першої стратегії першим гравцем, через д(д_ь Ц₂, ■ ••, Яв) - змішану стратегію другого гравця. Побудуємо графіки середніх виграшів першого гравця (рис. 9.2.), для цього знайдемо М| (рО:

Рис. 6.2

М1 (р ) = (12 - 3)Р1 + 3 = 9Р1 + 3; М₂ (р )=(9 - 5)р, + 5 = 4_А + 5; М 3 (р1) = (7 - б)р1 + 6 = р1 + 6; М 4 (р1) = (5 - 8)р1 + 8 = -3 р_х + 8; М₅ (р_х ) = (4 - 9)р1 + 9 = -5р1 + 9; М₆ (р ) = (2 - 10)р1 +10 = -8_А +10.

Нижня границя множини обмежень зображена на рис. 6.2

*

жирною лінією. Як бачимо, тахМ (р₁) досягається в точці М, що утворюється лініями М₁(р₁) і М₄(^₁). Покладемо д₂= д₃= д₅= #₆=0. Для знаходження р₁, р₂, д_ь д₄, V необхідно розв'язати такі системи рівнянь:

¹² р, + ³ р 2 = V

⁵ р1 + ⁸р 2 = ^V,

12^ + 3# ₄ = V

5д₁ + 8# ₄ = V,

д ₂ =^{1 -}

27

7

А = ^{1 -} р 2 ^, Розв'язками цих систем буде: 5 7 5

млн. грн.

12 '² 12 12 4

Ми отримали такий оптимальний розв'язок. Підприємству необхідно 5/12 обсягів сировини використати на виготовлення першого виду продукції, а 7/12 - для другого виду продукції. При цьому отримаємо максимальний прибуток у розмірі 6.75 млн. грн.

; р 2

; Чх

; ? 4

^р1

V

6.5. Зведення задач теорії ігор до задач лінійного програмування

Розглянемо матричну гру п х т,

г * і * * * \ *

Позначимо через р = (,р*,...,р_п),# = (д^ ,#₂,...,^) імовірності

оптимальних змішаних стратегій відповідно першого та другого гравців, а через V- ціну гри. Без доведення сформулюємо теорему.

Теорема. Для того, щоб число V було ціною гри, а р і д - векторами ймовірностей оптимальних стратегій, необхідне й достатнє виконання системи нерівностей:

(6.8)

^ а_ур* > V, і = 1, т,

і =1

[а, ].

задану матрицею

/ * * * \ ⁽^*^, Я 2 Ят ⁾

т

^ а_Гд* < V, і = 1,п.

(6.9)

І=1

Для простоти припустимо, що V > 0. Цього завжди можна досягнути завдяки додаванню до всіх елементів матриці [а_і] ] одного й

того ж постійного числа к. Така процедура не вплине на оптимальні стратегії, а тільки збільшить ціну гри на к.

Мета першого гравця полягає в отриманні максимального виграшу, а другого - мінімального програшу. Користуючись сформульованою теоремою, задачу максимізації гарантованого виграшу першого гравця і задачу мінімізації гарантованого програшу другого гравця можна представити як пару взаємно двоїстих задач лінійного програмування: Завдання І гравця

Г7*

(6.і0)

7 = V ^ тах

X ^ауР * > V У = І^т

і=і

п

ЇР* = і

і=і

Р* > 0, і = і, п. Завдання ІІ гравця

Т-г*

(6.іі)

ґ = V ^ тіп

X а^] < V, і = і, п

і=і

т

X?* = і

]=і

#* > 0, ] = і, т.

Запишемо систему обмежень (6.і0) у розширеній формі:

* * *

^аііРі + ^а2іР* + ". + ^апіР* > ¹

^: , , , > (6.і2)

а, Р, + а₂ Р₂ +... + а Р > V

іт-Г і 2т^ 2 пт^п

* * *

Рі + Р * + ... + Р_п = ^і. Поділимо праву й ліву частину нерівності на V. Отримуємо:

(6.і3)

^аіі Рі* ^{/ V} + ^а 2і Р 2 ^{/ V} + ... + ^апі Р* ^/ ^^ > ^{V / V}

* * * а. Р. / V + а₂ Р₂ / V +... + а Р > V/ V

іт^ і 2т^ 2 пт^ п

Р* / V + Р 2 / V + ... + Р*_п/ V = і/V

Р

Зробимо заміну: —- = х_г, і = і, п. Маємо:

а_ітх_і + а_2тх₂ +... + а_птх_п > і.

Яп (і, ]) 47

Оскільки метою першого гравця є максимальний виграш, то він має забезпечити тіп -. Отже, визначення оптимальної стратегії для

V

першого гравця зводиться до вирішення такої задачі лінійного програмування:

знайти 7 = х_і + х₂ +... + х_п ^ тіп при виконанні умов

а_ііх +... + а _і х > і

іі і пі п

' + + > і (6.і5)

а_і х_і +... + а х > і

іт і пт п

х_г > 0, і = і, п.

Аналогічні міркування можна провести відносно задачі другого

*

гравця. Виконавши заміну — = у., отримаємо наступну задачу:

V ^]

знайти Р = у_і + у₂ +... + у_т ^ тах при виконанні умов

^аііуі + ... + ^аітУт < ^і

' , (6і6)

а_і у_і +... + а у < і

піУ і птУ п

у > 0, і = і, т.

Задача другого гравця є двоїстою до задачі першого гравця.

Процес знаходження розв'язку гри з використанням лінійного програмування складається з таких етапів:

1. - побудова пари двоїстих задач лінійного програмування, еквівалентних даній матричній грі;

2. - знаходження оптимальних планів пари двоїстих задач;

3. - знаходження розв'язку гри, використовуючи співвідношення між планами двоїстих задач і оптимальними стратегіями та ціною гри.

а_л, х_л ++ х₀ ... а , х > і

іі і 2і 2 пі п

(6.і4)

Приклад 6.3. Дві фірми можуть вкласти свій наявний капітал у будівництво п'яти об'єктів. Стратегія фірм: і-та стратегія полягає у

фінансуванні і-го об'єкту (і = 1, 2, ...,5). Враховуючи особливості вкладів й інші умови, прибуток фірми виражається за допомогою матриці А:

2	0	1	-3	4
0	- 2	-1	4	3
2	0	3	2	-1
0	-3	1	0	1
3	0	0	-2	2

А =

Прибуток першої фірми є величиною збитку другої, тобто дану гру можна розглядати як гру двох осіб з нульовою сумою.

Розв'язання. Для зведення даної задачі до задачі лінійного програмування необхідно, насамперед, до кожного елементу матриці додати число к = 4 (необхідно, щоб усі елементи матриці А були додатніми). Отримуємо:

6	4	5	1	8
4	2	3	8	7
6	4	7	6	3
4	1	5	4	5
7	4	4	2	6

А =

Вводимо невідомі величини х₁, х₂ задачу лінійного програмування: знайти

х₅. Тоді отримуємо таку

7 = х₁ + х₂ + х₃ + х₄ + х₅ ^ тіп

при виконанні умов

6х₁ + 4х₂ + 6х₃ + 4 х₄ + 7 х₅ > 1

4х₁ + 2х₂ + 4х₃ + х₄ + 4х₅ > 1

5х₁ + 3х₂ + 7х₃ + 5х₄ + 4х₅ > 1

х₁ + 8х₂ + 6х₃ + 4х₄ + 2х₅ > 1

8х₁ + 7х₂ + 3х₃ + 5х₄ + 6х₅ > 1

х, > 0, і = 1,5.

Розв'язком цієї задачі буде

х₁ = 0; х ₂ = 0; х₃ = 0.125; х ₄ = 0; х₅ = 0.125.

Оскільки х1 х2 х3 х4 х5 — , то

V

1

1

1

V =

= 4.

0.125 + 0.125 0.25

Рг

Знаючи те, що х_{ = —, отримуємо: р_{ = х_{ • V;р₁ = 0;р₂ = 0;

V

рз = 0.5; р4 = 0; р5 = 0.5.

Побудуємо до даної задачі двоїсту. За невідомі візьмемо у₁, у₂ Уз, :у4, У5. Маємо

Р = У1 + У2 + Уз + У4 + У5 ^ ^тах

при виконанні умов

6У1 + 4у2 + 5ухз + у4 + 8У5 < 1

4 У1 + 2 у 2 + з уз + 8 у 4 + 7 у 5 < 1

6. у1 + 4 у 2 + 7 у з + 6 у 4 + з у 5 < 1 4у1 + у 2 + 5 у з + 4 у 4 + 5 у 5 < 1

7. у1 + 4 у 2 + 4 у з + 2 у 4 + 6 у 5 < 1 у, > 0, і = 15.

Розв'язком цієї задачі

у1 = 0; у 2 = 0.25; у з = 0; у 4 = 0; у 5 = 0. Користуючись

Я

уі

знайдемо:

V

я, = у, • ^Я1 =⁰;я2 =¹;Яз = я4 = я_ь =⁰. Отже, вектори ймовірностей оптимальних змішаних стратегій відповідно для першої та другої фірми будуть: р = (0; 0; 0.5; 0; 0.5); д = (0; 1; 0; 0;0), а ціна початкової гри V* = V - 4 = 0.

1 '

7