Двойной интеграл в полярной системе координат
Полярная система координат считается заданной, если заданы:
1) точка 0, называемая полюсом;
2) полуось 0х, называемая полярной осью. На 0х выбрана масштабная единица.
Тогда
положение точки М
в
полярной системе координат определяют
две величины:
–
угол наклона вектора
к полярной оси 0х
и
–
величина
вектора
(Рис.
5).
Рис. 5
Если задать декартовую систему координат, связанную с полярной так, чтобы ось 0х совпадала с полярной осью 0х и ось 0у была перпендикулярна к полярной оси 0х, то можно установить связь между координатами точки М в обеих системах координат:
или
,
где
(x;y)
–
координаты точки М
в
декартовой системе,
–
координаты той же точки М
в полярной системе.
Любую
кривую
,
заданную
в декартовой системе координат, можно
задать в полярной системе уравнением
,
которое можно получить непосредственно
исходя из геометрических свойств этой
кривой либо с помощью формул перехода
от декартовых координат к полярным.
Элементарной
областью D
в полярной системе координат считают
сектор, ограниченный двумя лучами,
исходящими из полюса под углами
и
к оси 0x
(
и
),
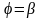и кривой
(рис.6).
Рис. 6
Определение. Область D в полярной системе координат называется правильной, если любой луч, исходящий из полюса и проходящий через внутреннюю точку области D, пересекает границу области D только в двух точках (рис. 7).
Рис. 7
Замечание
1.
Если полюс
0 лежит вне области D,
то
правильную область D
в
полярной системе координат можно описать
как область, ограниченную двумя лучами
и
и кривыми
и
при
.
Замечание
2.
Если полюс
0 лежит внутри области D,
то
правильную область D
в
полярной системе координат можно описать
неравенствами:
Переход от декартовых координат к полярным в двойном интеграле проводится для упрощения его вычисления в случае, если:
1)
функция
зависит
от
или от
,
так как
и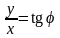
;
2) область D ограничена кривыми, уравнения которых легко преобразуются в полярные координаты.
Теорема (переход от декартовых координат к полярным в двойном интеграле)
Пусть выполнены условия:
непрерывна в замкнутой области D;
область D является правильной в полярной системе координат, т.е.
область
D
задана
неравенствами:
,
;
функци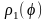и
и
непрерывны при
.
Тогда справедливо равенство:
Следует помнить правило этого перехода:
Заменить
и
в функции
и
в
уравнениях границ области D;Заменить
;При вычислении двойного интеграла в полярных координатах внешний интеграл вычисляется по от до , а внутренний по от до – если полюс 0 лежит вне области D. Если полюс 0 лежит внутри области D, то внешний интеграл по от 0 до
,
а внутренний по
от 0
до
(граница области D).
Пример.
Вычислить
,
если D:
Чертёж области D:
– круг с центром в точке (1;0) и радиусом r = 1 (рис. 8).
Рис. 8
В полярной системе координат:
уравнение
преобразуется к виду:
прямая
;
(рис.
8).
Ответ:
.