Предел функции в точке
Определение 12
Число
А
называется пределом функции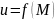 
в точке
,
если для любого сколь угодно малого
числа 
найдется число 
такое, что для любой точки 
,
находящейся в проколотой
-окрестности
точки
,
выполняется неравенство: 
.
Этот факт записывается так:
.
Для функции двух переменных это определение можно сформулировать следующим образом:
Число
А называется пределом
функции
в точке
,
если для любого сколь угодно малого
числа
найдётся число
такое, что для любой точки 
,
находящейся в проколотой
-окрестности
точки
,
выполняется неравенство:
.
Этот факт записывается так:
Замечание
3.
и
в
окрестности точки
может
происходить
в
различных
направлениях.
При
этом предел функции существует, если
в различных направлениях предел один
и тот же. В противном случае говорят,
что функция в точке
предел
не имеет.
Пример 3. Вычислить предел:
Пример
4.
Вычислить предел:
т.е.
предел функции зависит от направления
стремления (х;у)
к (0;0), следовательно предел не существует.
Замечание
4.
Аналогично с определениями, данными
для функции одной переменной, можно
дать определения для пределов: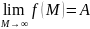 
и
Непрерывность функции. Точки разрыва
Определение 13
Функция
называется непрерывной
в точке
,
если предел этой функции в точке
равен значению функции в точке 
:
Определение 14
Функция
называется
непрерывной
в некоторой области
,
если она непрерывна в каждой точке этой
области
.
Определение 15
Точки, в которых функция не является непрерывной, называются точками разрыва функции.
Пример
5.
Исследовать функцию на непрерывность:
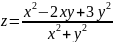
Решение.
D(z)
:
В области определения D(z) функция z непрерывна, так как является элементарной функцией. В точке (0;0) функция не определена, следовательно, эта точка разрыва функции.
Пример
6.
Исследовать функцию на непрерывность:
Решение.
D(z)
:
Так
как функция z
элементарная то в области определения
D(z)
она является непрерывной. Но при условии
функция не определена, следовательно,
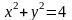
есть линия разрыва этой функции
(окружность с центром в точке (0;0) и
радиусом 2).
Замечание. Теоремы о конечных пределах и свойства непрерывных функций на замкнутых областях, сформулированные ранее для функции одной переменной, обобщаются на случай функции нескольких переменных.
§2. Дифференцирование функции нескольких переменных
1. Частные производные функции нескольких переменных
Рассмотрим
функцию двух переменных
.
Пусть
точки
Определение 1
Если
x
и у
получают приращения
и
соответственно, то функция
может получать приращения трёх видов:
– частное
приращение функции по х;
– частное
приращение функции по у;
–
полное
приращение функции по х
и у.
Определение 2
Частной
производной по х
функции
в точке (х;у)
называется предел отношения частного
приращения функции по х
к приращению
при условиях, что
и этот предел существует, т. е. :
где
или
– обозначения частной производной по
х.
Определение 3
Частной
производной по у
функции
в точке (х;у)
называется предел отношения частного
приращения функции по у
к приращению
при условиях, что
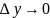и этот предел существует, т.е. :
где
и
– обозначения частной производной по
у.
Замечание 1. Частные приращения по х и по у находятся при неизменных переменных x и у соответственно. Поэтому правила нахождения частных производных по х и по у являются обычными правилами дифференцирования функции одной переменной в предположении, что переменные х и у соответственно остаются постоянными.