5. Дифференцирование функции одной и двух переменных, заданных неявно

Определение 6

Пусть дано уравнение . Считается, что функция задана неявно в области уравнением , если для

любого значения найдётся одно число – такое, что

.

Теорема 7 (дифференцирование функции одной переменной, заданной неявно)

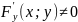Пусть функция задана неявно уравнением , где функция дифференцируема в точке и . Тогда существует производная .

Доказательство: Если для и , то

⇒ ⇒ , так как

Что и требовалось доказать.

Определение 7

Пусть дано уравнение . Считается, что функция задана неявно в области уравнением , если для любой пары найдётся одно число такое, что .

Теорема 8 (дифференцирование функции двух переменных, заданных неявно)

Пусть функция задана неявно уравнением , где функция 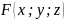дифференцируема в точке и . Тогда существуют частные производные функции , по х и у, которые равны:

и .

Доказательство: Из определения неявного задания функции

⇒ .

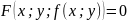Поэтому

⇒ ⇒ ,

так как .

Что и требовалось доказать.

Аналогично выводится формула для .

5. Частные производные и дифференциалы высших порядков

Пусть функция в каждой точке некоторой области имеет частные производные Они представляют собой функции двух переменных. Производные от этих функций, если они существуют, называются частными производными второго порядка и обозначаются:

,

,

,

.

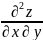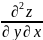Частные производные второго порядка вида и называют смешанными производными.

Теорема 9 (о равенстве смешанных производных)

Пусть в области существуют смешанные производные

и в точке они непрерывные. Тогда .

Замечание 2. Аналогично определяются частные производные второго, третьего и т.д. порядков. И смешанные производные в точках их непрерывности тоже равны. Определенный в пункте 4 дифференциал для функции : называют дифференциалом первого порядка. Пусть функции дифференцируемы в некоторой области . Тогда в этой области определен и дифференциал второго порядка: , если непрерывны в области D.

5. Аналитический признак полного дифференциала

Теорема 10 (аналитический признак полного дифференциала)

Чтобы выражение было полным дифференциалом некоторой функции для , необходимо и достаточно выполнения следующих условий:

1. непрерывны в области

2. .

Необходимость. Дано: непрерывны в области и существует функция для которой

.

Доказать, что для .

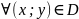Доказательство: Так как , то

Тогда

= , = .

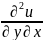Так как по условию 1 и непрерывны в области то непрерывны

и ⇒ .

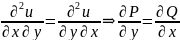Что и требовалось доказать.

Достаточность. Дано: и непрерывны в области и для .

Доказать, что существует функция для которой

.

Доказательство: Проверим, можно ли найти функцию сли и выполнены условия теоремы

(1)

. (2)

Из (1) следует: если у =const. Тогда

(3)

Приравнивая (2) и (3) получим:

(4)

так как по условию теоремы.

Следовательно:

т.е. не зависит от х.

⇒

Значит, функцию можно найти из условий теоремы и выражения (1):

Что и требовалось доказать.