
- •Глава 1. Дифференциальное исчисление функции многих переменных §1. Понятие функции нескольких переменных
- •Пространство и множества в пространстве
- •Определение функции нескольких переменных
- •Линии и поверхности уровня
- •Предел функции в точке
- •Непрерывность функции. Точки разрыва
- •§2. Дифференцирование функции нескольких переменных
- •1. Частные производные функции нескольких переменных
- •2. Дифференцируемость функции двух переменных
- •3. Дифференцирование сложной функции
- •4. Дифференциал функции двух переменных
- •Дифференцирование функции одной и двух переменных, заданных неявно
- •Частные производные и дифференциалы высших порядков
- •Аналитический признак полного дифференциала
- •§3. Производная по направлению и градиент
- •1. Производная по направлению
- •2. Градиент и его свойства
- •§4. Экстремумы функций нескольких переменных
- •Экстремумы функций двух и трёх переменных
- •Условный экстремум
- •Глава 2. Интегральное исчисление функции нескольких переменных § 1. Двойной интеграл
- •Геометрическая задача, приводящая к понятию двойного интеграла
- •3. Геометрический смысл двойного интеграла
- •4. Основные свойства двойного интеграла
- •Геометрический смысл теоремы о среднем значении двойного интеграла
- •5. Вычисление двойного интеграла в декартовых координатах
- •Двойной интеграл в полярной системе координат
- •7. Интеграл Эйлера–Пуассона
- •8. Некоторые приложения двойного интеграла
- •§2. Тройной интеграл
- •1. Определение тройного интеграла
- •2. Физический и геометрический смысл тройного интеграла
- •3. Основные свойства тройного интеграла
- •4. Вычисление тройного интеграла в декартовой системе координат
- •Основные свойства криволинейного интеграла I рода
- •2. Криволинейный интеграл II рода (по координатам)
- •Свойства криволинейного интеграла II рода
- •2.2. Физический смысл криволинейного интеграла II рода
- •2.3. Вычисление криволинейного интеграла II рода
- •3. Формула Грина
- •4. Независимость криволинейного интеграла от пути интегрирования (случай на плоскости)
- •5. Потенциальное поле, потенциальная функция и её вычисление
- •6. Вычисление криволинейного интеграла, независящего от пути интегрирования
- •§ 4. Поверхностные интегралы
- •1. Поверхностный интеграл I рода
- •2. Поверхностный интеграл II рода
- •3. Дивергенция векторного поля. Теорема Гаусса–Остроградского
- •4. Ротор (вихрь) векторного поля. Теорема Стокса
§4. Экстремумы функций нескольких переменных
Экстремумы функций двух и трёх переменных
Определение 1
Точка
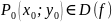 называется
точкой максимума функции
,
если
для любых точек
называется
точкой максимума функции
,
если
для любых точек
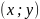 ,
принадлежащих
окрестности точки
,
выполняется неравенство:
,
принадлежащих
окрестности точки
,
выполняется неравенство:
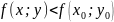 .
.
Определение 2
Точка
называется
точкой минимума функции
,
если
для любых точек
,
принадлежащих окрестности точки
,
выполняется
неравенство:
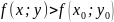 .
.
Определение 3
Точки максимума и минимума называются точками экстремума функции.
Теорема 1 (необходимое условие экстремума)
Если точка является точкой экстремума функции , то её частные производные в точке равны нулю или не существуют.
При доказательстве теоремы 1 используются определения частных производных и теорема о необходимых условиях экстремума функции одной переменной.
Замечание 1. Аналогично формулируются определения 1 и 2 и теорема 1 для функции трёх и более переменных.
Теорема 2 (достаточные условия экстремума функции двух переменных)
Если
функция
дважды дифференцируема в критической
точке
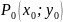 и её окрестности и определитель
и её окрестности и определитель
 ,
то в точке
есть экстремум. Причём, если
,
то в точке
есть экстремум. Причём, если
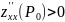 ,
то точка
является точкой минимума функции, а
если
,
то точка
является точкой минимума функции, а
если
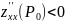 ,
то точка
является точкой максимума.
Замечание
2.
Если определитель
,
то точка
является точкой максимума.
Замечание
2.
Если определитель
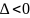 ,
то в точке
нет экстремума, при этом точку
называют седловой точкой. Если
,
то в точке
нет экстремума, при этом точку
называют седловой точкой. Если
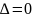 ,
то вопрос об экстремуме в точке
остаётся нерешённым, нужны исследования
функции
по её производным более высокого порядка.
,
то вопрос об экстремуме в точке
остаётся нерешённым, нужны исследования
функции
по её производным более высокого порядка.
Теорема 3 (достаточные условия экстремума функции трёх переменных)
Пусть
функция
дважды дифференцируема в
критической точке
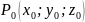 и её окрестности. Определитель
и её окрестности. Определитель
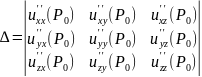 имеет все главные диагональные миноры
имеет все главные диагональные миноры
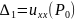 ,
,
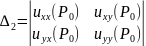 ,
,
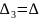 положительные, то
–точка минимума функции
.
Если
положительные, то
–точка минимума функции
.
Если
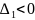 ,
,
 и
и
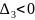 , то точка
– точка максимума функции
.
, то точка
– точка максимума функции
.
Замечание
3.
Если
критическая точка функции
и
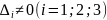 ,
но не выполняются условия теоремы 3, то
в точке
нет экстремума, при этом точка
называется седловой точкой. Если все
,
но не выполняются условия теоремы 3, то
в точке
нет экстремума, при этом точка
называется седловой точкой. Если все
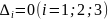 ,
то вопрос об экстремуме в точке
решается с помощью производных более
высокого порядка.
,
то вопрос об экстремуме в точке
решается с помощью производных более
высокого порядка.
Пример
1.
Найти экстремумы функции:
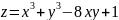 .
.
Решение.
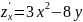 ;
;
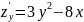 .
.
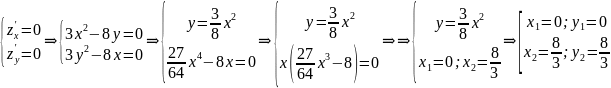 .
.
Получили
две точки
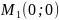 и
и
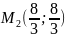
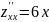 ;
;
 ;
;

а) Исследуем точку :
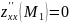 ;
;
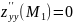 ;
;
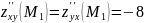 .
.
Тогда
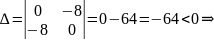 точка
точка
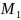 не является точкой экстремума.
не является точкой экстремума.
б)
Исследуем точку
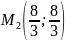 :
:
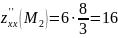 ;
;
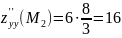 ;
;
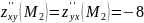 .
.
Тогда
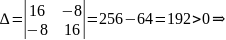 точка
точка
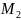 является точкой экстремума. Причём так
как
является точкой экстремума. Причём так
как
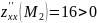 ,
то точка
является точкой минимума функции:
,
то точка
является точкой минимума функции:
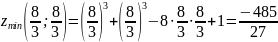 .
.
Ответ:
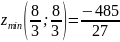
Условный экстремум
Пусть
задана функция
на множестве
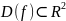 .
Требуется найти экстремумы функции
.
Требуется найти экстремумы функции
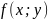 ,
если
,
если
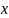 и
и
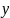 связаны некоторым условием
связаны некоторым условием
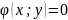 ,
называемым уравнением
связи.
,
называемым уравнением
связи.
Определение
4.
Точка
называется точкой
условного экстремума
функции
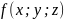 при выполнении дополнительных условий
– уравнений связи.
при выполнении дополнительных условий
– уравнений связи.
Для нахождения точек условного экстремума существует два метода: метод прямого отыскания и метод Лагранжа. Прямой метод состоит в том, что из уравнения связи выражается одна из переменных через другую, и её подставляют в функцию . Получают функцию одной переменной, для которой и решают задачу нахождения обычного экстремума. Такой метод применяют тогда, когда удаётся из уравнения связи выразить одну переменную через другую.
Пример
2.
Найти условный экстремум функции
при
условии
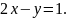 Решение.
Используем метод прямого отыскания
точек условного экстремума. Из условия
Решение.
Используем метод прямого отыскания
точек условного экстремума. Из условия
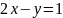 выразим
выразим
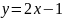 и подставим его в функцию
.
Тогда
и подставим его в функцию
.
Тогда
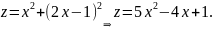
Найдём
для функции
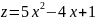 обычный экстремум.
обычный экстремум.
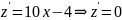 ,
,



 – +
x
– +
x
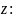
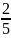
Следовательно,
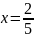 – точка минимума функции
.
– точка минимума функции
.
Подставляем в функцию и получим:
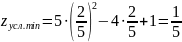 .
.
Ответ:
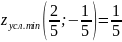 .
.
Определение
5.
Функция
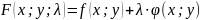 называется функцией
Лагранжа,
а коэффициент λ
–
множителем
Лагранжа.
называется функцией
Лагранжа,
а коэффициент λ
–
множителем
Лагранжа.
Замечание
4.
Если связи не одно уравнение, а несколько
(например,
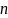 ),
то функция Лагранжа для функции
записывается с
множителями Лагранжа:
),
то функция Лагранжа для функции
записывается с
множителями Лагранжа:
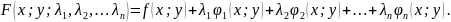
Теорема 4 (необходимое условие поиска условного экстремума)
Пусть
функции
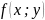 и
и
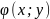 ,
дифференцируемые в точке
,
дифференцируемые в точке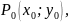 а
является точкой условного экстремума
функции
при условии
.
Тогда найдется такое число
а
является точкой условного экстремума
функции
при условии
.
Тогда найдется такое число
 ,
при котором точка
является критической для функции
Лагранжа
,
при котором точка
является критической для функции
Лагранжа
 .
.
Метод Лагранжа поиска условного экстремума состоит в следующем:
1)
составляют функцию Лагранжа
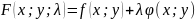 ;
;
2)
находят её частные производные по
 ;
;
3) приравнять частные производные к нулю и решают систему уравнений
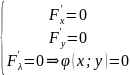 ;
;
4)
исследуют найденную в результате решения
системы точку
при найденном значении
и решают задачу обычного экстремума
для
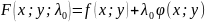 .
.
Теорема 5 (достаточное условие поиска условного экстремума для случая одного уравнения связи)
Пусть
точка
и
найдены из решения системы
 .
.
Пусть
определитель
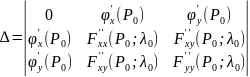 .
.
Если
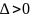 ,
то функция
имеет в точке
условный максимум.
,
то функция
имеет в точке
условный максимум.
Если , то функция имеет в точке условный минимум.
Пример 3. Методом Лагранжа найти условный экстремум для функции при условии . Решение. Составим функцию Лагранжа
 .
.
Найдём её частные производные по :
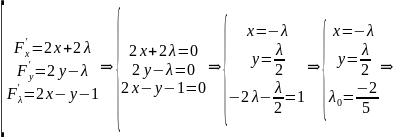
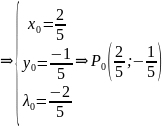 при
при
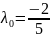 .
.
Выясним
характер точки
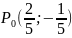 по теореме 5:
по теореме 5:
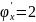 ;
;
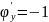 ;
;
 ;
;
 ;
;
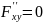 .
.
Составим определитель:
 .
.
Так как , то – точка условного минимума.
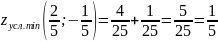 .
.
Ответ: .
