5. Потенциальное поле, потенциальная функция и её вычисление
Определение
6.
Векторное
поле
называется потенциальным,
если
не зависит от пути, соединяющего точки
A
и
B.
Если не зависит от пути интегрирования, то
При
этом функция
называется потенциальной
функцией
поля
.
Вычисление потенциальной функции
Если , то существует функция , для которой
.
Для вычисления функции
используем криволинейный интеграл
,
не зависящий от пути интегрирования.
Путь AB
выбираем любой, соединяющий точки
и
;
например, ломаную линию ACB,
где
(рис. 3). Тогда
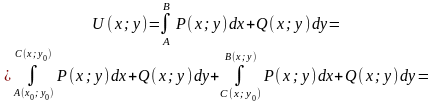
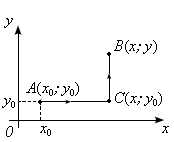
Рис. 3
Итак,
Пример.
Найти потенциальную функцию
по её полному дифференциалу:
Проверим условие полного дифференциала:
– выполняется.
Способ
1.
Если
,
то
Следовательно,
Способ
2.
Выберем в качестве пути интегрирования
ломаную OCB,
где
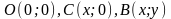(рис.
4)
Рис. 4
Итак:
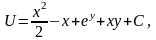где
C
– произвольная постоянная.
6. Вычисление криволинейного интеграла, независящего от пути интегрирования
Интеграл
не зависит от пути интегрирования, если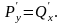
Тогда значение интеграла будет зависеть
от координат начала пути – точка A
и конца пути – точка B.
При этом интеграл записывают следующим
образом:
Чтобы его вычислить, можно использовать
два способа.
Способ 1.
где
– потенциальная функция.
Но
так как
,
то
Следовательно
Способ
2.
Можно вычислить интеграл, выбрав любой
путь интегрирования, соединяющий точки
и
.
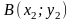Наиболее рационально выбрать путь ACB
(рис. 3)
–
ломаную линию, звенья которой параллельны
осям координат, т.е. взять точку
или
,
тогда путь интегрирования будет состоять
из двух отрезков: AC
и
CB,
при
этом интеграл будет равен сумме двух
интегралов
по
AC
и
CB.
0
Пример. Вычислить интеграл
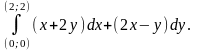
Способ 1 (рис. 5).
Рис.
5
Способ 2.
,
где
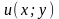
функция, для которой
.
Значит:
Ответ: 8.
§ 4. Поверхностные интегралы
1. Поверхностный интеграл I рода
Пусть
функция
непрерывна на гладкой поверхности S,
заданной функцией
непрерывно дифференцируемой в каждой
точке области D
R2.
Определение.
Поверхностным
интегралом I
рода
от функции
по поверхности S
называется предел интегральной суммы
при условиях:
1)
и
(стягиваясь в точку);
2) предел интегральной суммы существует и не зависит ни от способа разбиения поверхности S на n частей, ни от выбора точек на этих частях, т.е.
где
– площадь i-й
части поверхности
– дифференциал поверхности S,
вычисляемый по формуле:
Если проекция поверхности S на плоскость OXY однозначна и совпадает с областью D, то поверхностный интеграл I рода вычисляется по формуле:
Замечание 1. Если прямая, параллельная оси OZ и проходящая через внутреннюю точку области D, пересекает поверхность S в более чем одной точке, то поверхность S разбивается на части так, чтобы прямая, параллельная оси OZ, пересекала поверхность S только в одной точке. Далее интегрирование следует выполнить по каждой из полученных частей.
Замечание 2. Поверхностный интеграл I рода не зависит от того, по какой стороне поверхности он берётся.
Замечание 3. Физический смысл поверхностного интеграла I рода зависит
от физического смысла данного скалярного поля, т.е. от , он может определять массу, распределенную на данной поверхности, электрический заряд и т.д.
Замечание
4.
Если функция
равна единице во всех точках поверхности
S,
то поверхностный интеграл I рода
равен площади поверхности
S.
Следовательно,
справедлива формула:
где D – проекция поверхности S на плоскость OXY, – функция, задающая поверхность S.