3. Формула Грина
Теорема.
Пусть C
– граница замкнутой области
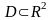и функции
,
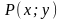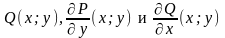и
непрерывны в области D.
Тогда справедлива формула
Грина:
,
где обход контура C осуществляется против часовой стрелки.
Доказательство: Пусть область D правильная в направлениях 0X и 0Y (рис. 1).
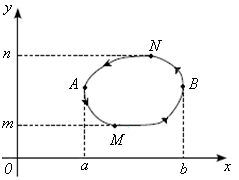
Рис. 1
Пусть
кривая AMB
– график функции
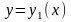– дуга AMB,
кривая
ANB
– график
функции
–
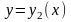дуга ANB,
кривая
MAN
– график
функции
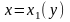– дуга MAN,
кривая
MBN
– график
функции
–
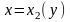дуга MBN.
Вычислим
т.е.
.
(1)
Аналогично вычислим
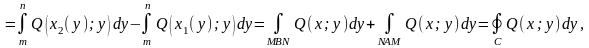
т.е.
.
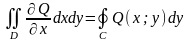(2)
Вычтем (1) из (2), получим:
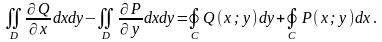
Используя свойства двойного и криволинейного интегралов, можно записать:
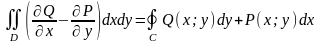
или
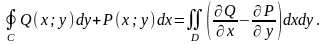
Теорема доказана.
Замечание 1. Условия теоремы Грина обеспечивают существование всех входящих в неё интегралов.
Замечание 2. Если область D не является правильной, то её надо разбить на правильные части. Тогда:
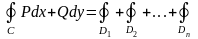
и для каждого из n слагаемых применяем формулу Грина.
Пример 1. Вычислить по формуле Грина:
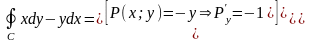
Из полученного результата можно записать формулу для вычисления площади области D, у которой границей является контур C, с помощью криволинейного интеграла:
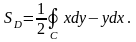
Пример 2. Вычислить по формуле Грина:
.
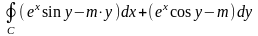окружность
с центром
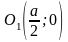и
радиусом
,
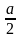m,
a
постоянные величины.
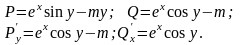
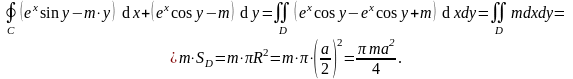
Ответ:
4. Независимость криволинейного интеграла от пути интегрирования (случай на плоскости)
Определение. Криволинейный интеграл II рода называется независящим от пути интегрирования, если результат интегрирования будет один и тот
же по любому пути, соединяющему точки A и B, на котором функции P (x;y) и Q (x;y) непрерывны. Обозначение такого интеграла:
Теорема
1.
Криволинейный интеграл
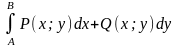не зависит от пути интегрирования в
области D
тогда
и только тогда, когда
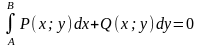
по любому замкнутому контуру C, целиком лежащему в области D.
Доказательство:
Необходимость.
Дано:
,
где С – любой контур
.
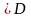Доказать:
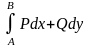не зависит от пути интегрирования.
Пусть
точки A
и
.
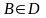Рассмотрим две произвольные кривые
и
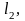соединяющие
точки A
и
B
(рис. 1).
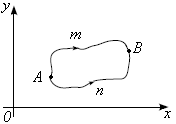
Рис. 1
Так как по условию не зависит от пути интегрирования, то
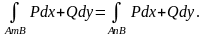
Отсюда следует:
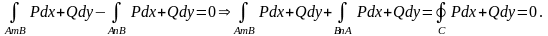
Так как кривые и взяты произвольно, то и контур C=AmBnA – произвольный. Необходимость доказана.
Достаточность. Дано: , где С – любой контур .
Доказать: не зависит от пути интегрирования.
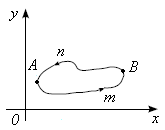
Рис. 2
Возьмём
произвольный контур
и на нём две точки A
и
B
(произвольно) (рис. 2). Тогда по свойству
криволинейного интеграла можно записать:
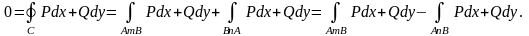
Поэтому
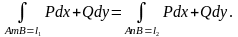
Как видим, результат интегрирования по двум произвольным кривым, имеющих одно и тоже начало (A) и один и тот же конец (B) одинаковый, следовательно, не зависит от пути интегрирования.
Достаточность доказана.
Теорема 2 (критерий независимости криволинейного интеграла от пути интегрирования)
Пусть
функции
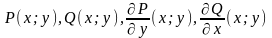непрерывны в односвязной области D
R2.
Чтобы интеграл
не зависел от пути интегрирования в
области D,
необходимо и достаточно выполнение
равенства:
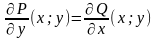в
любой точке
.
Доказательство:
Необходимость.
Дано:
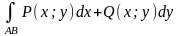не
зависит от пути интегрирования в области
D,
т.е. по любому контуру
Доказать:
в любой точке
.
Предположим,
что в точке
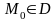равенство не выполняется, т.е.
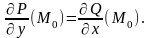
Пусть
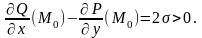Построим окружность C
с центром в точке
столь малого радиуса
,
чтобы во всех точках круга S,
ограниченного этой окружностью,
выполнялось неравенство
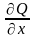
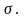Это требование можно выполнить исходя
из непрерывности функции
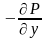.Тогда
по формуле Грина:
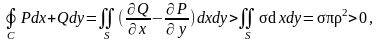
т.е.
есть замкнутый контур, принадлежащий
области D,
по которому интеграл не равен 0. Это
противоречит условию теоремы.
Следовательно, в любой точке
выполняется равенство:
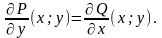Что и требовалось доказать.
Достаточность.
Дано:
в
любой точке
Доказать:
не
зависит от пути интегрирования в области
D,
т.е. по любому контуру
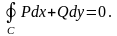
Рассмотрим
любой контур
,
ограничивающий область
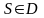(так как область D
односвязная). Тогда по формуле Грина:
.
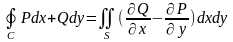Так
как по условию теоремы
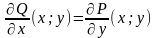в любой точке
то
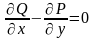в области
.
Следовательно,
Так
как контур C
произвольный в области D,
то
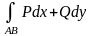в области D
не
зависит от пути интегрирования.
Достаточность доказана.