
- •Глава 1. Дифференциальное исчисление функции многих переменных §1. Понятие функции нескольких переменных
- •Пространство и множества в пространстве
- •Определение функции нескольких переменных
- •Линии и поверхности уровня
- •Предел функции в точке
- •Непрерывность функции. Точки разрыва
- •§2. Дифференцирование функции нескольких переменных
- •1. Частные производные функции нескольких переменных
- •2. Дифференцируемость функции двух переменных
- •3. Дифференцирование сложной функции
- •4. Дифференциал функции двух переменных
- •Дифференцирование функции одной и двух переменных, заданных неявно
- •Частные производные и дифференциалы высших порядков
- •Аналитический признак полного дифференциала
- •§3. Производная по направлению и градиент
- •1. Производная по направлению
- •2. Градиент и его свойства
- •§4. Экстремумы функций нескольких переменных
- •Экстремумы функций двух и трёх переменных
- •Условный экстремум
- •Глава 2. Интегральное исчисление функции нескольких переменных § 1. Двойной интеграл
- •Геометрическая задача, приводящая к понятию двойного интеграла
- •3. Геометрический смысл двойного интеграла
- •4. Основные свойства двойного интеграла
- •Геометрический смысл теоремы о среднем значении двойного интеграла
- •5. Вычисление двойного интеграла в декартовых координатах
- •Двойной интеграл в полярной системе координат
- •7. Интеграл Эйлера–Пуассона
- •8. Некоторые приложения двойного интеграла
- •§2. Тройной интеграл
- •1. Определение тройного интеграла
- •2. Физический и геометрический смысл тройного интеграла
- •3. Основные свойства тройного интеграла
- •4. Вычисление тройного интеграла в декартовой системе координат
- •Основные свойства криволинейного интеграла I рода
- •2. Криволинейный интеграл II рода (по координатам)
- •Свойства криволинейного интеграла II рода
- •2.2. Физический смысл криволинейного интеграла II рода
- •2.3. Вычисление криволинейного интеграла II рода
- •3. Формула Грина
- •4. Независимость криволинейного интеграла от пути интегрирования (случай на плоскости)
- •5. Потенциальное поле, потенциальная функция и её вычисление
- •6. Вычисление криволинейного интеграла, независящего от пути интегрирования
- •§ 4. Поверхностные интегралы
- •1. Поверхностный интеграл I рода
- •2. Поверхностный интеграл II рода
- •3. Дивергенция векторного поля. Теорема Гаусса–Остроградского
- •4. Ротор (вихрь) векторного поля. Теорема Стокса
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Российский химико-технологический университет
им. Д. И. Менделеева
Дифференциальное и интегральное исчисление функции многих переменных
Утверждено Редакционным советом
университета в качестве учебного пособия
Москва
2011
УДК 517 (075)
ББК 22.161.1
Р83
Авторы: Е. Г. Рудаковская, М. Ф. Рушайло, Е. Ю. Напеденина,
М. А. Меладзе, Т. В. Хлынова
Рецезент:
Доктор технических наук, профессор Российского химико-технологического университета
им. Д. И. Менделеева
Л. С. Гордеев
Дифференциальное и интегральное исчисление функции многих
Р83 переменных: учеб. пособие / сост.:
Е. Г. Рудаковская, М. Ф. Рушайло, Е. Ю. Напеденина, М. А. Меладзе, Т. В. Хлынова, под ред. Е. Г. Рудаковской, М. Ф. Рушайло. – М. : РХТУ им. Д. И. Менделеева, 2011. – 92 с.
ISBN 978-5-7237-0937-9
Пособие представляет сжатое изложение лекций по математическому анализу, читаемых кафедрой высшей математики для студентов первого курса всех факультетов и колледжей РХТУ им. Д.И. Менделеева.
Пособие охватывает следующие разделы курса математического анализа: дифференциальное исчисление функций нескольких переменных, интегральное исчисление функций нескольких переменных. Большое внимание уделено разбору примеров по изучаемым темам, имеющим прикладное значение для других дисциплин.
УДК 517(075) ББК 22.161.1
ISBN 978-5-7237- 0937-9 © Российский химико-технологический
университет им. Д. И. Менделеева, 2011
ОГЛАВЛЕНИЕ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ 1
РОССИЙСКОЙ ФЕДЕРАЦИИ 1
Российский химико-технологический университет 1
им. Д. И. Менделеева 1
Дифференциальное и интегральное исчисление функции многих переменных 1
Глава 1. Дифференциальное исчисление функции многих переменных 7
§1. Понятие функции нескольких переменных 7
1. Пространство и множества в пространстве 7
2. Определение функции нескольких переменных 9
3. Линии и поверхности уровня 10
4. Предел функции в точке 11
5. Непрерывность функции. Точки разрыва 13
§2. Дифференцирование функции нескольких переменных 14
1. Частные производные функции нескольких переменных 14
2. Дифференцируемость функции двух переменных 15
3. Дифференцирование сложной функции 17
4. Дифференциал функции двух переменных 19
5. Дифференцирование функции одной и двух переменных, заданных неявно 20
6. Частные производные и дифференциалы высших порядков 22
7. Аналитический признак полного дифференциала 23
§3. Производная по направлению и градиент 25
1. Производная по направлению 25
2. Градиент и его свойства 28
§4. Экстремумы функций нескольких переменных 31
1. Экстремумы функций двух и трёх переменных 31
2. Условный экстремум 34
Глава 2. Интегральное исчисление функции нескольких переменных 38
§ 1. Двойной интеграл 38
1. Геометрическая задача, приводящая к понятию двойного интеграла 38
3. Геометрический смысл двойного интеграла 40
4. Основные свойства двойного интеграла 41
5. Вычисление двойного интеграла в декартовых координатах 43
6. Двойной интеграл в полярной системе координат 50
7. Интеграл Эйлера–Пуассона 55
8. Некоторые приложения двойного интеграла 57
§2. Тройной интеграл 58
1. Определение тройного интеграла 58
2. Физический и геометрический смысл тройного интеграла 59
3. Основные свойства тройного интеграла 60
4. Вычисление тройного интеграла в декартовой системе координат 61
5. Вычисление тройного интеграла в цилиндрических координатах 64
6. Вычисление тройного интеграла в сферических координатах 64
7. Некоторые приложения тройного интеграла 65
§ 3. Криволинейные интегралы 66
1. Криволинейные интегралы I рода (по дуге) 66
2. Криволинейный интеграл II рода (по координатам) 69
3. Формула Грина 74
4. Независимость криволинейного интеграла от пути интегрирования (случай на плоскости) 77
5. Потенциальное поле, потенциальная функция и её вычисление 83
6. Вычисление криволинейного интеграла, независящего от пути интегрирования 86
§ 4. Поверхностные интегралы 88
1. Поверхностный интеграл I рода 88
2. Поверхностный интеграл II рода 90
3. Дивергенция векторного поля. Теорема Гаусса–Остроградского 95
4. Ротор (вихрь) векторного поля. Теорема Стокса 97
Глава 1. Дифференциальное исчисление функции многих переменных 5
§1. Понятие функции нескольких переменных 5
1. Пространство
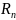 и множества в пространстве
5
и множества в пространстве
5
2. Определение функции нескольких переменных 6
3. Линии и поверхности уровня 7
4. Предел функции в точке 8
5. Непрерывность функции. Точки разрыва 9
§2. Дифференцирование функции нескольких переменных 10
1. Частные производные функции нескольких переменных 10
2. Дифференцируемость функции двух переменных 11
3. Дифференцирование сложной функции 13
4. Дифференциал функции двух переменных 15
5. Дифференцирование функции одной и двух переменных, заданных неявно 16
6. Частные производные и дифференциалы высших порядков 18
7. Аналитический признак полного дифференциала 19
§3. Производная по направлению и градиент 21
1. Производная по направлению 21
2. Градиент и его свойства 24
§4. Экстремумы функций нескольких переменных 27
Экстремумы функций двух и трёх переменных 27
Условный экстремум 30
Глава 2. Интегральное исчисление функции нескольких переменных 33
§1. Двойной интеграл 33
Геометрическая задача, приводящая к понятию двойного интеграла 33
2. Определение двойного интеграла 35
3. Геометрический смысл двойного интеграла 36
4. Основные свойства двойного интеграла 36
5. Вычисление двойного интеграла в декартовых координатах 36
6. Двойной интеграл в полярной системе координат 36
7. Интеграл Эйлера–Пуассона 36
8. Некоторые приложения двойного интеграла 36
§2. Тройной интеграл 36
1. Определение тройного интеграла 36
2. Физический и геометрический смысл тройного интеграла 36
3. Основные свойства тройного интеграла 36
4. Вычисление тройного интеграла в декартовой системе координат 36
5. Вычисление тройного интеграла в цилиндрических координатах 36
6. Вычисление тройного интеграла в сферических координатах 36
7. Некоторые приложения тройного интеграла 36
§3. Криволинейные интегралы 36
1. Криволинейные интегралы I рода (по дуге) 36
2. Криволинейный интеграл II рода (по координатам) 36
3. Формула Грина 36
4. Независимость криволинейного интеграла от пути интегрирования (случай на плоскости) 36
5. Потенциальное поле, потенциальная функция и её вычисление 36
6. Вычисление криволинейного интеграла, независящего от пути интегрирования 36
§4. Поверхностные интегралы 36
1. Поверхностный интеграл I рода 36
2. Поверхностный интеграл II рода 36
3. Дивергенция векторного поля. Теорема Гаусса–Остроградского 36
4. Ротор (вихрь) векторного поля. Теорема Стокса 36
Глава 1. Дифференциальное исчисление функции многих переменных §1. Понятие функции нескольких переменных
Пространство и множества в пространстве
Определение 1
Пространством
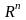 называется множество групп
называется множество групп
 из
“n”
действительных чисел. Такое множество
групп из “n”
чисел отождествляют с множеством точек
из
“n”
действительных чисел. Такое множество
групп из “n”
чисел отождествляют с множеством точек
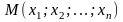 .
При этом числа
.
При этом числа
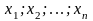 называют координатами точек М,
а число “n”
определяет размерность пространства
.
называют координатами точек М,
а число “n”
определяет размерность пространства
.
В частности:
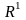 =
R
–
одномерное пространство множества
точек М
(х);
=
R
–
одномерное пространство множества
точек М
(х);
 –
двухмерное
пространство множества точек М
(х;у);
–
двухмерное
пространство множества точек М
(х;у);
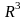 –
трёхмерное
пространство множества точек М
(x;y;z).
–
трёхмерное
пространство множества точек М
(x;y;z).
Определение 2
Множеством D (или областью) в пространстве называют любую часть пространства .
Определение 3
δ-окрестностью
точки 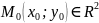
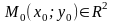 называют множество точек
называют множество точек

 ,
для которых выполняется неравенство:
,
для которых выполняется неравенство: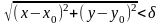 ,
т. е. любая окружность с радиусом, равным
δ, и с центром в точке
,
т. е. любая окружность с радиусом, равным
δ, и с центром в точке 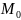
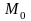 .
Причём, если δ-окрестность точки
.
Причём, если δ-окрестность точки
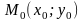
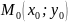 проколотая
(т.е.
не включается), то её аналитическая
запись :
проколотая
(т.е.
не включается), то её аналитическая
запись :
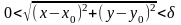 .
.
Аналогично,
если точка 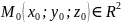
![]()
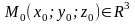 ,
то её δ-окрестность –
,
то её δ-окрестность –
множество
точек 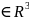
 ,
для которых выполняется неравенство:
,
для которых выполняется неравенство:
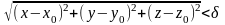
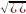 ,
т. е. любой шар с радиусом, равным δ, и с
центром в точке
,
т. е. любой шар с радиусом, равным δ, и с
центром в точке
![]() .
Тогда проколотая δ-окрестность точки
.
Тогда проколотая δ-окрестность точки
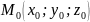
![]()
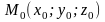 :
:
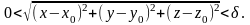
Определение 4
Точка
называется внутренней
точкой
области 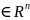
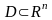 ,
если
,
если
найдётся такая δ-окрестность точки , все точки которой принадлежат области D.
Определение 5
Точка
называется граничной
точкой
области
![]() ,
если в любой δ-окрестности точки
есть точки, принадлежащие D
и не принадлежащие D.
,
если в любой δ-окрестности точки
есть точки, принадлежащие D
и не принадлежащие D.
Определение 6
Множество D называется открытым, если все его точки являются внутренними.
Определение 7
Множество D называется замкнутым, если оно содержит все свои граничные точки.
Определение 8
Множество D называется односвязным, если любые его две точки можно соединить непрерывной кривой, принадлежащей D.
Определение функции нескольких переменных
Определение 9
Если
для множества 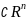 по некоторому правилу функция f
по некоторому правилу функция f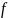 в каждой точке
в каждой точке
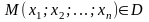 соответствует
единственное число
соответствует
единственное число
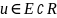
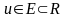 ,
то говорят, что на множество D
определена функция
,
то говорят, что на множество D
определена функция
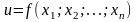
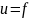 .
Причём, область D
– это область определения функции
.
Причём, область D
– это область определения функции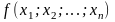 ,
а область E
– это область изменения этой функции
(или
область её значений).
,
а область E
– это область изменения этой функции
(или
область её значений).
Замечание 1. Во многих прикладных задачах термин функция заменяется термином скалярное поле ,
т.е.
точке 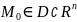
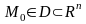 соответствует скаляр (число)
соответствует скаляр (число) 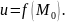
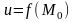 .
.
Замечание 2. Изобразить графически функцию “n” переменных возможно только для n=2. Это будет некоторая поверхность в трёхмерном пространстве.
Линии и поверхности уровня
Определение 10
Линией
уровня
для функции
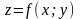 называется
множество точек
называется
множество точек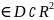
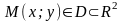 ,
при которых функция принимает одно и
то же значение, т.е.:
,
при которых функция принимает одно и
то же значение, т.е.:
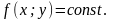
Определение 11
Поверхностью
уровня
для функции 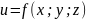
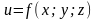 называется множество точек
называется множество точек 
 ,
при которых функция принимает одно и
то же значение, т.е.
,
при которых функция принимает одно и
то же значение, т.е.
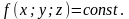
Пример
1.
Для функции 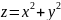
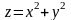 линиями уровня будут окружности
линиями уровня будут окружности 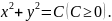
 .
.
Пример
2.
Для
функции
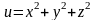 поверхностями уровня будут сферы
поверхностями уровня будут сферы
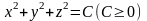 .
.
Замечание
1.
По
аналогии можно определить поверхности
уровня для 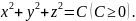
функций любого числа переменных.
Замечание 2. В ряде случаев можно получить представление о характере изменения функции по линиям или поверхностям уровня.
