Геометрический смысл теоремы о среднем значении двойного интеграла

Если в области D, то объём цилиндроида можно заменить на объём цилиндра, у которого основаниями верхним и нижним будет область D, а высота .

5. Вычисление двойного интеграла в декартовых координатах

Определение 1. Замкнутая область D называется правильной в направлении оси 0y (или 0x), если любая прямая, проходящая через внутреннюю точку области D и параллельная оси 0y (или 0x), пересекает границу области D только в двух точках.

Рис. 2

На рисунках: а – D правильная в направлении 0y; б – D правильная в направлении 0x; в – D правильная в направлении 0x, но неправильная в направлении 0y; г – D правильная в направлении 0y, но неправильная в направлении 0x.

При вычислении двойного интеграла используют правила сведения этого интеграла к повторному. При этом область D должна быть правильной в направлении, например оси 0y и её границы должны описываться непрерывными функциями, причём – нижняя граница области D и – верхняя граница области D, т.е. для любого .

Если эти условия на область D не выполняются, то её разбивают на части, на которых эти условия выполняются, и интегрируют по каждой из частей, а затем результат суммируют.

Далее рассматривают при некотором фиксированном значении 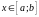интеграл от функции f (x;y) по :

Тогда объём цилиндроида равен

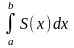При этом вычисляется при фиксированном х (x=const) и называется внутренним интегралом, а – внешним интегралом.

– повторный интеграл.

Правило вычисления начинается с вычисления внутреннего интеграла при х = const, затем от полученной функции S(x) вычисляется внешний интеграл .

Рассмотрим случай сведения двойного интеграла к повторному, если

область D правильная в направлении оси 0x и границы её заданы непрерывными функциями: x=ψ₁(y) – левая граница области D и x=ψ₂(y) – правая граница области D, т.е. ψ₁(y) ≤ ψ₂(y) для любого y [c;d].

Далее при некотором фиксированном значении y [c;d] рассматривают интеграл от функции f (x;y) при x [ψ₁(y);ψ₂(y)]:

Тогда объём цилиндроида равен:

При этом вычисляется при фиксированном значении y (y=const) и называется внутренним интегралом, а – внешним интегралом.

Правило вычисления этого повторного интеграла аналогично описанному выше: сначала вычисляют внутренний интеграл по х при y = const, затем – внешний интеграл по y.

Замечание 1. Если область D является правильной в направлении обеих осей и границы описываются следующим образом: нижняя граница: ; верхняя граница: ; x [a;b]; левая граница: x=ψ₁(y); правая граница: x=ψ₂(y); y [c;d], то выполняется равенство:

Общеупотребительна другая запись повторных интегралов:

или

Замечание 2. При представлении двойного интеграла в виде повторного, пределы внешнего интеграла всегда постоянные, а пределы внутреннего интеграла, как правило, переменные. Только в случае если область D – прямоугольник и , , то внешний и внутренний интегралы имеют постоянные пределы:

Замечание 3. Если и область D – прямоугольник: , , то двойной интеграл от по такой области D равен произведению определённых интегралов:

Пример 1. Вычислить повторный интеграл:

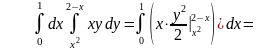
Ответ: .

Пример 2. Расставить пределы интегрирования в различном порядке:

, если область D ограничена линиями: y = 2x; y = x; x = 1.

1) Чертёж области D:

Рис. 3

2) Область D правильная в направлении оси 0y для x [0;1] .

Нижняя граница D : y = x; верхняя граница D : y = 2x. Поэтому:

3) Область D правильная в направлении оси 0X, но для левая граница D: ; правая граница D: 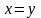, а для левая граница D: ; правая граница D: . Поэтому область D в этом случае разбиваем на две области прямой y=1: и , интеграл по области D представляем суммой по областям и :

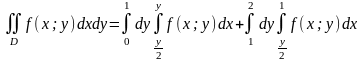
Ответ:

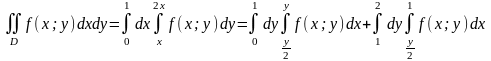
Пример 3. Изменить порядок интегрирования:

Чертёж области D: , нижняя граница области D: , верхняя граница (рис. 4).

Рис. 4

Чтобы изменить порядок интегрирования, надо внешний интеграл взять по y, а внутренний – по x. Область D в направлении оси 0x правильная, но для левая граница области D: х = 1 – у, правая граница х = 1, а для левая граница D: х = у – 1, правая – та же Поэтому область D разбиваем на две области прямой y = 1: и и интеграл по области D представляем в виде суммы интегралов по областям и :

Ответ: