Глава 2. Интегральное исчисление функции нескольких переменных § 1. Двойной интеграл

1. Геометрическая задача, приводящая к понятию двойного интеграла

Пусть на замкнутой области D R² задана непрерывная функци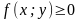я для . В системе координат 0XYZ функция задаёт некоторую поверхность . Из каждой граничной точки области D восстанавливаем перпендикуляры к плоскости 0XY до пересечения с поверхностью . При этом в пространстве R³ получаем объёмное цилиндрическое тело, у которого нижним основанием является область D, верхним – часть поверхности и боковая поверхность параллельна оси 0Z. Такое тело будем называть цилиндроидом.

Ставим задачу: вычислить объём V этого цилиндроида (рис. 1). С этой целью проведём следующие операции: а) область D разделим на n частей (произвольно) – б) обозначим площади каждой из этих частей в) на каждой из частей разбиения области D выберем точку и строим ряд цилиндрических «столбиков», имеющих основания и высоты ;

Рис. 1

г) вычислим объёмы полученных «столбиков»:

д) в результате построено тело, состоящее из n «столбиков», приближенно равное объёму цилиндроида, который равен:

е) для повышения точности равенства: будем уменьшать размеры частей разбиения области D, увеличивая их количество, т.е. n → ∞, но при условии стремления к нулю max , стягивающегося в точку. Тогда можно записать точное равенство:

ж) этот предел и даёт объём V заданного цилиндроида.

2. Определение двойного интеграла Определение 1. Сумма , построенная в разделе 1 пункт д) называется интегральной суммой для функции на замкнутой

области D.

Определение 2. Двойным интегралом от функции по замкнутой области D называется предел интегральной суммы при условиях:

а) n → ∞ и max → 0 (стягиваясь в точку);

б) этот предел существует и не зависит ни от способа разбиения области D на части, ни от выбора на этих частях точек

Обозначение двойного интеграла:

Теорема (достаточное условие существования двойного интеграла)

Если в замкнутой области D R² функция непрерывна, то двойной интеграл от этой функции по области D существует.

3. Геометрический смысл двойного интеграла

1) Если функция непрерывна в области D R² и f(x;y) ≥ 0, то двойной интеграл от этой функции по области D равен объёму цилиндроида, у которого нижнее основание – область , верхнее – часть поверхности и боковая поверхность параллельна 0Z, т.е.

2) Если для любых , то двойной интеграл от z = 1 по области D равен площади области D:

.

4. Основные свойства двойного интеграла

1) Пусть функция непрерывна в области D R², причём , тогда

Это свойство, как и последующие, можно доказать путём рассмотрения интегральных сумм и последующего перехода к пределам.

2. Постоянный множитель k выносится за знак двойного интеграла:

2. Двойной интеграл от суммы конечного числа функций равен сумме двойных интегралов от этих функций:

2. Если для двух непрерывных в области D функций f(x;y) и g(x;y) выполняется неравенство f(x;y) ≤ g(x;y), то

.

Теорема (о среднем значении двойного интеграла)

Если функция непрерывна в замкнутой области D, то внутри области D найдется, хотя бы одна точка , в которой выполняется равенство:

где – площадь области D.

Доказательство: По свойству непрерывной функции в замкнутой области, функция в области D достигает своих наименьшего (m) и наибольшего (M) значений. Значит:

m ≤ f (x;y) ≤ M для .

Тогда для всех можно записать

m ≤ ≤ M ,

где

Умножая последнее неравенство на , получим:

Суммируем все n неравенств ( ):

Вынесем m и М за знаки сумм (как постоянные величины) и перейдём к пределам при n → ∞ и max ∆S_i → 0 (стягиваясь в точку):

Ссылаемся на определение двойного интеграла и получаем:

РРРРазделим последнее неравенство на , где . Тогда

По свойству непрерывной функции в замкнутой области, функция в области D принимает все промежуточные значения между наименьшим (m) и наибольшим (М) значениями. Следовательно, существует точка , в которой:

Теорема доказана.