2. Дифференцируемость функции двух переменных

Определение 4

Функция называется дифференцируемой в точке 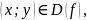если её полное приращение в этой точке можно представить в виде:

,

где А и В не зависят от и , а , при

Теорема 1 (связь между дифференцируемостью и существованием частных производных)

Если функция дифференцируема в точке , то в этой точке существует её частные производные и . Доказательство: функция дифференцируема в точке , следовательно

где , при , т. е. и .

Пусть , тогда Разделим на и вычислим предел:

следовательно существует и .

Аналогично при : . Разделим на и вычислим предел:

следовательно существует и .

Теорема 2 (достаточные условия дифференцируемости функции)

Пусть функция в некоторой точке имеет непрерывные в этой точке частные производные и 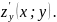Тогда

функция дифференцируема в этой точке.

Теорема 3 (связь дифференцируемости и непрерывности функции)

Если функция дифференцируема в точке , то она непрерывна в этой точке.

Доказательство: , где А и В не зависят от и , , т.е. и , тогда , следовательно непрерывна в этой точке.

3. Дифференцирование сложной функции

Теорема 4 (полная производная)

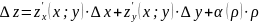Пусть функция дифференцируема в точке и функции дифференцируемы в соответствующей точке t при которой . Тогда сложная функция дифференцируема в точке t, причём – полная производная для при . Доказательство: , где , при , т. е. и .

Разделим на и вычислим предел при

Так как , то

Итак,

– полная производная для функции .

Теорема 5 (дифференцирование сложной функции)

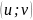Пусть функция дифференцируема в точке , а функции дифференцируемы в точке , соответствующей точке = ( Тогда сложная функция дифференцируема в точке , причём:

,

.

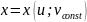Формулы этой теоремы следуют из условия, что находится при поэтому функции и от одной переменной, следовательно, можно воспользоваться для вывода формулы

теоремой 4.

Аналогично, при выводе формулы для используется условие, что , т.е. функции рассматриваются как функции одной переменной, т.е. можно использовать теорему 4.

4. Дифференциал функции двух переменных

Определение 5

Если функция дифференцируема в точке , то где при .

Тогда первые два слагаемых, линейные относительно и , называются дифференциалом функции в точке , т. е. .

Если х и у независимые переменные, то и . Тогда другая запись дифференциала функции двух переменных в точке : .

Так как и при , то – бесконечно малая величина при более высокого порядка малости по

сравнению с , то между можно поставить знак приближённого

равенства ⇒ – формула

приближённых вычислений.

Теорема 6 (свойство инвариантности дифференциала)

Пусть функция дифференцируема в точке ,

а функции дифференцируемы в точке , соответствующей точке Функция является сложной функцией переменных , дифференцируемой по переменным . Тогда запись дифференциала функции z по переменным х и у та же, что и по переменным :

.

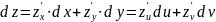Доказательство:

⇒

Что и требовалось доказать.