2. Поверхностный интеграл II рода
Гладкая
поверхность
называется двусторонней,
если нормаль к этой поверхности в любой
её точке при обходе по любому замкнутому
контуру, лежащему на поверхности S
и не имеющему общих точек с её границей,
возвращается в первоначальное положение.
Выбор определённой стороны поверхности,
т.е. выбор направления нормали к
поверхности, называется ориентацией
поверхности.
Пусть
гладкая ориентированная поверхность,
в каждой точке которой задана непрерывная
функция
.
Разобьём поверхность S
на n
частей произвольно и каждую часть
проецируем на плоскость, например, OXY.
Обозначим площадь каждой проекции
.
На каждой из частей поверхности
произвольно берём точку
и составим сумму
.
Определение. Поверхностным интегралом II рода называется предел интегральной суммы при условиях: 1) и (стягиваясь в точку),
2)
предел интегральной суммы существует
и не зависит ни от способа разбиения
поверхности S
на
части, ни от выбора точек
на каждой из частей поверхности, т.е.
.
Аналогично можно дать определения поверхностных интегралов II рода по другим координатам:
и
.
Пусть в каждой точке ориентированной поверхности определен вектор
где
непрерывные функции на поверхности S.
Тогда можно определить поверхностный
интеграл II рода в общем случае от
векторной функции
по поверхности
:
где
скалярное произведение вектора
и
вектора
с координатами:
Следовательно, поверхностный интеграл II рода в общем случае
можно записать:
т.е.
в общем случае интеграл можно записать
как поверхностный интеграл I рода или
как поверхностный интеграл II рода (по
координатам). Поверхностный интеграл
II рода называют потоком
векторного поля
через
поверхность
или
.
Название «поток» связано с гидромеханической
задачей – вычисления количества жидкости
или газа, протекающего в заданном
направлении в единицу времени через
поверхность S.
Переход к другой стороне поверхности
меняет направление нормали к поверхности,
а потому
и знак поверхностного интеграла II рода.
Вычисление поверхностного интеграла
II рода сводится к вычислению поверхностного
интеграла I рода:
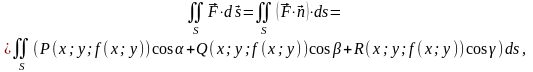
где
направляющие косинусы вектора
нормали
;
функция, задающая поверхность S.
Или вычисление поверхностного интеграла II рода сводится к вычислению суммы трёх двойных интегралов:
где ПрyzS, ПрxzS, ПрxyS проекции поверхности S на плоскости OYZ, OXZ и OXY соответственно, функции x(y;z), y(x;z) и z(x;y) – выражения, полученные из уравнения , задающего поверхность S, с помощью разрешения x, y и z относительно соответствующих координат.
Пример.
Вычислить поток вектора
через внешнюю сторону
сферы,
лежащей в первом октанте (рис. 1):
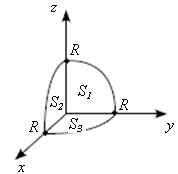
Рис. 1
Так как в первом октанте внешняя нормаль сферы со всеми осями координат образует острые углы, то все три направляющих косинуса нормали неотрицательны. Поэтому:
Вычислим первый интеграл, остальные будут по величине такие же.
Итак:
Ответ:
