1. Основные свойства криволинейного интеграла I рода

1. Криволинейный интеграл I рода не зависит от направления пути интегрирования:

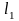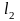2. Если дугу l интегрирования разбить на две части и , то:

3)

4) где k=const.

5) Если для любой точки кривой AB, то – длина дуги AB.

Пример 1. Вычислить длину кривой от точки A (0;0) до точки B(4;8).

Ответ:

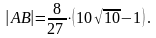
Пример 2. Вычислить , если AB – отрезок прямой от точки A (0;0) до точки B(4;3). Прямая AB y = kx (x = 4 и y = 3):

,

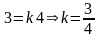т.е. уравнение прямой AB

Ответ: .

2. Криволинейный интеграл II рода (по координатам)

Пусть в пространстве задана дуга AB гладкой кривой l и на этой дуге AB задано векторное поле

Точками дуга AB разбита на n произвольных дуг , на каждой из которых произвольно взяты

точки . Концы дуг соединены отрезками прямых, на которых выбрано направление, т.е. образованы векторы: каждый из которых имеет координаты: .

Составим сумму скалярных произведений векторов :

.

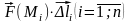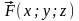Определение 3. Сумма называется интегральной суммой для векторной функции по дуге AB кривой .

Определение 4. Криволинейным интегралом II рода от векторной функции по дуге AB кривой называется предел последовательности интегральных сумм при условиях: 1) и ;

2) этот предел существует и не зависит ни от способа разбиения дуги на части, ни от выбора на каждой из этих частей точек . Этот криволинейный интеграл II рода обозначается:

т.е. :

.

Теорема 1 (существование криволинейного интеграла II рода)

Если вектор-функция непрерывна на дуге AB гладкой кривой l, то криволинейный интеграл II рода существует. Замечание 1. Если вектор-функция задана на дуге AB гладкой кривой , то криволинейный интеграл II рода записывается следующим образом:

1. Свойства криволинейного интеграла II рода

1. Интеграл II рода изменяет знак на противоположный при изменении направления пути интегрирования:

.

2. 

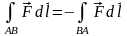Остальные свойства аналогичные свойствам интеграла I рода.

2.2. Физический смысл криволинейного интеграла II рода

Интеграл равен работе, совершаемой при перемещении материальной точки единичной массы из точки A в точку B по кривой l в силовом поле, создаваемом вектором .

2.3. Вычисление криволинейного интеграла II рода

Пусть дуга AB кривой задаётся параметрически: x= x(t), y= y(t),

z = z(t) и точке A соответствует значение параметра , а точке B – значение . Тогда: y x

В частном случае плоского задания кривой , например, в виде функции от точки до точки , интеграл II рода вычисляется по формуле:

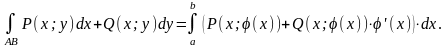
Пример 1. Вычислить:

Ответ: 0.

Пример 2. Вычислить:

Ответ: .

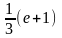Пример 3. Вычислить работу силового поля 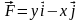при перемещении материальной точки вдоль верхней половины эллипса из точки в точку .

Ответ:

Замечание 2. Если кривая l, по которой проводится интегрирование, является замкнутой, то A= B (начало пути совпадает с его концом). Тогда путь интегрирования называют контуром и обозначают буквой C. При криволинейный интеграл обозначают:

с указанной стрелкой направления интегрирования. В таком случае интеграл называют циркуляцией вектора по замкнутому контуру. Если нет стрелки, указывающей направление, то вычисляют интеграл против часовой стрелки (положительное направление).